Интервалы возрастания и убывания функции
С помощью данного сервиса можно найти интервалы возрастания и убывания функции в онлайн режиме с оформлением решения в Word.
- Решение онлайн
- Видеоинструкция
Исследование функции с помощью производной
Определение: Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)>f(x).
Определение: Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)<f(x).
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Точками экстремума могут служить только критические точки I рода, т.е. точки, принадлежащие области определения функции, в которых производная f′(x) обращается в нуль или терпит разрыв.
Правило нахождения экстремумов функции y=f(x) с помощью первой производной
- Найти производную функции f′(x).
- Найти критические точки по первой производной, т.е. точки, в которых производная обращается в нуль или терпит разрыв.
- Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции f(x). Если на промежутке f′(x)<0, то на этом промежутке функция убывает; если на промежутке f′(x)>0, то на этом промежутке функция возрастает.
- Если в окрестности критической точки f′(x) меняет знак с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.
- Вычислить значения функции в точках минимума и максимума.
С помощью приведенного алгоритма можно найти не только экстремумы функции, но и промежутки возрастания и убывания функции.
Пример №1: Найти промежутки монотонности и экстремумы функции: f(x)=x3–3x2.
Решение: Найдем первую производную функции f′(x)=3x2–6x.
Найдем критические точки по первой производной, решив уравнение 3x2–6x=0; 3x(x-2)=0 ;x = 0, x = 2
Исследуем поведение первой производной в критических точках и на промежутках между ними.
| x | (-∞, 0) | 0 | (0, 2) | 2 | (2, +∞) |
| f′(x) | + | 0 | — | 0 | + |
| f(x) | возрастает | max | убывает | min | возрастает |
f(0) = 03 – 3*02 = 0
f(2) = 23 – 3*22 = -4
Ответ: Функция возрастает при x∈(-∞ ; 0)∪(2; +∞); функция убывает при x∈(0;2);
точка минимума функции (2;-4); точка максимума функции (0;0).
Правило нахождения экстремумов функции y=f(x) с помощью второй производной
- Найти производную f′(x).
- Найти стационарные точки данной функции, т.е. точки, в которых f′(x)=0.
- Найти вторую производную f″(x).
- Исследовать знак второй производной в каждой из стационарных точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то – минимум. Если же вторая производная равна нулю, то экстремум функции надо искать с помощью первой производной.
- Вычислить значения функции в точках экстремума.
Отсюда следует, что дважды дифференцируемая функция f(x) выпукла на отрезке [a, b], если вторая производная f»(x) ≥ 0 при всех х [a, b].
Все вычисления можно проделать в онлайн режиме.
Пример №2. Исследовать на экстремум с помощью второй производной функцию: f(x) = x2 – 2x — 3.
Решение: Находим производную: f′(x) = 2x — 2.
Решая уравнение f′(x) = 0, получим стационарную точку х=1. Найдем теперь вторую производную: f″(x) = 2.
Так как вторая производная в стационарной точке положительна, f″(1) = 2 > 0, то при x = 1 функция имеет минимум: fmin = f(1) = -4.
Ответ: Точка минимума имеет координаты (1; -4).
На этой странице вы узнаете
- Как мы ежедневно расставляем знаки неравенства в жизни?
- Как быстро определить верное обозначение точки на прямой?
- Как правильно чередовать знаки на числовой прямой?
Решая уравнение, мы стремимся к тому, чтобы обе части были равны. Но существуют такие примеры, где мы заведомо знаем, что два выражения не могут быть равны между собой. Они называются неравенствами.
Метод интервалов
Неравенство — это алгебраическое выражение, в котором одна сторона имеет отличное от другой значение. В неравенствах обычно одна сторона больше другой.
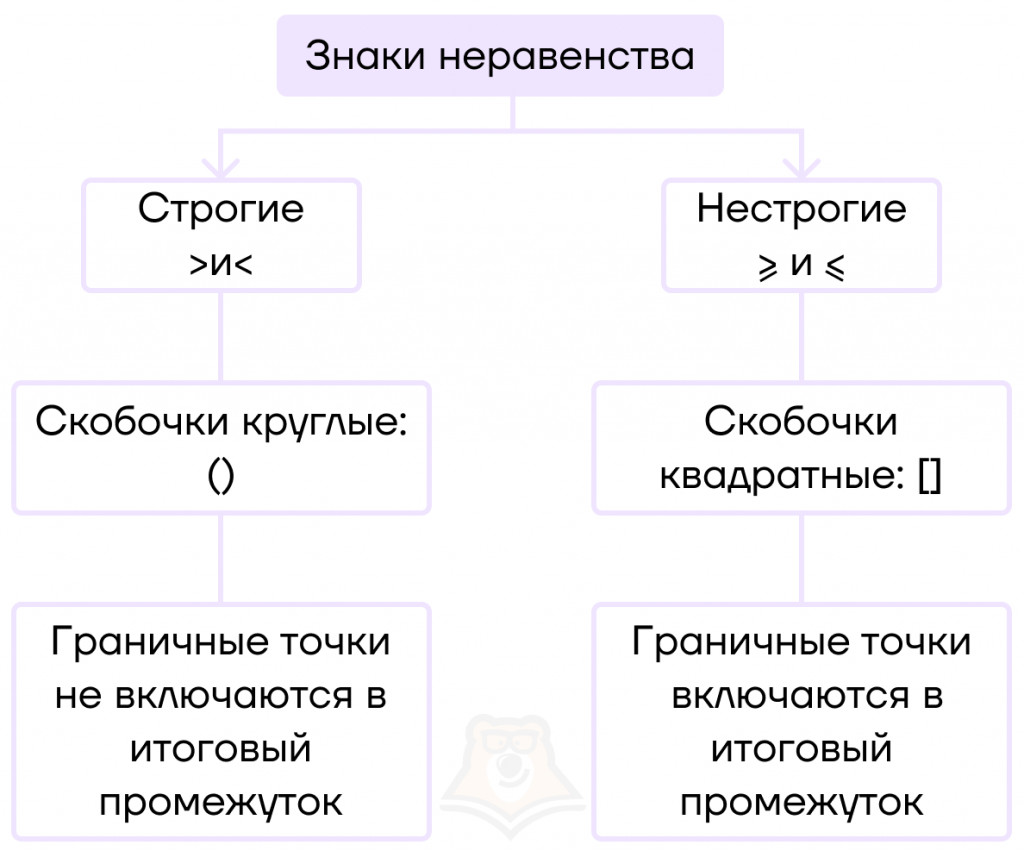
Для записи неравенств используют знаки > , < , ≥ , ≤ .
При этом “>” и “<” — это строгие знаки неравенства, а “≥” и “≤” — нестрогие знаки неравенства.
Их отличие в том, что нестрогие знаки неравенства включают граничные точки в итоговый промежуток, а строгие — нет.
Посмотрим на привычные ситуации с точки зрения строгости знаков неравенства.
Например, возьмем известную игру “Камень, ножницы, бумага”.
Правила игры говорят нам, что камень всегда побеждает ножницы, а бумага побеждает камень. Если перенести это на язык неравенства, то получится:
Теперь зайдем в магазин цифровой техники и попробуем выбрать себе новый мобильный телефон. Задачка непростая, не так ли? Две разные модели могут настолько незначительно отличаться друг от друга своими характеристиками, что будут казаться почти одинаковыми. Тогда мы можем сказать, что они практически равны между собой, то есть неравенство нестрогое. Но один из них всё-таки понравился нам больше.
И каждый наш выбор, каждый шаг – это расстановка знака неравенства в настоящей жизни. Просто по бокам от него не цифры и переменные, а существующие ситуации и вещи.
Рассмотрим пример неравенства (х — 10)(х + 21) > 0.

Его можно решить несколькими способами. Например, вспомним, что положительным будет произведение двух положительных или двух отрицательных множителей, тогда получается совокупность из двух систем.
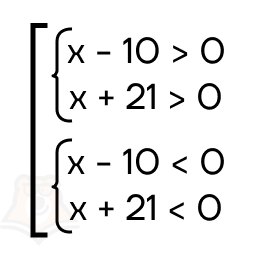
Однако этот способ решения очень трудоемкий и требует много времени. А если множителей будет больше, например, три или четыре, то время на решение в разы увеличивается.
Небольшой секрет тайм-менеджмента: как сократить время при решении неравенств? В таких случаях на помощь приходит метод интервалов.
Метод интервалов — специальный алгоритм решения для сложных неравенств вида f(x) > 0. При этом знак неравенства может быть любым.
Интервал — это промежуток на числовой прямой, ограниченный двумя различными числами.
Алгоритм решения неравенств методом интервалов
1 шаг. Перенести все части неравенства в одну сторону так, чтобы с другой остался только 0.
2 шаг. Найти нули функции, для этого необходимо решить уравнение f(x) = 0.
3 шаг. Начертить числовую прямую и отметить на ней все полученные корни. Таким образом, числовая прямая разобьется на интервалы.
4 шаг. Определить знаки на каждом интервале. Для этого необходимо подставить любое удобное значение в f(x) и определить, какой знак будет иметь функция на данном интервале.
Расставляя полученные корни на прямой, необходимо отмечать их точками. При этом от того, какая отмечена точка (выколотая или закрашенная), будет зависеть ответ.
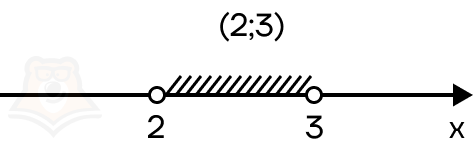
- Если в неравенстве стоит строгий знак неравенства, то все точки на прямой должны быть выколотыми.
Таким образом, граничные точки не будут включены в итоговый промежуток. Для записи таких точек используют круглые скобочки. Например, в промежуток (2;3) включаются все значения от 2 до 3, но не включаются граничные точки.
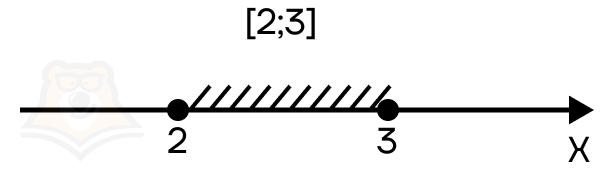
- Если в неравенстве стоит нестрогий знак неравенства, то найденные корни должны быть отмечены закрашенными точками.
Это означает, что мы включаем их в итоговый промежуток. Для записи таких точек используют квадратные скобочки. Например, в промежуток [2;3] включаются все значения от 2 до 3, в том числе и граничные точки.
- Если в неравенстве появляются ограничения и некоторые точки нельзя взять в ответ, то такие точки должны быть выколотыми на числовой прямой, при этом знак самого неравенства может быть как строгим, так и нестрогим.
Например, если необходимо решить неравенство с дробью, то нули знаменателя на числовой прямой обязательно должны быть обозначены выколотыми точками.
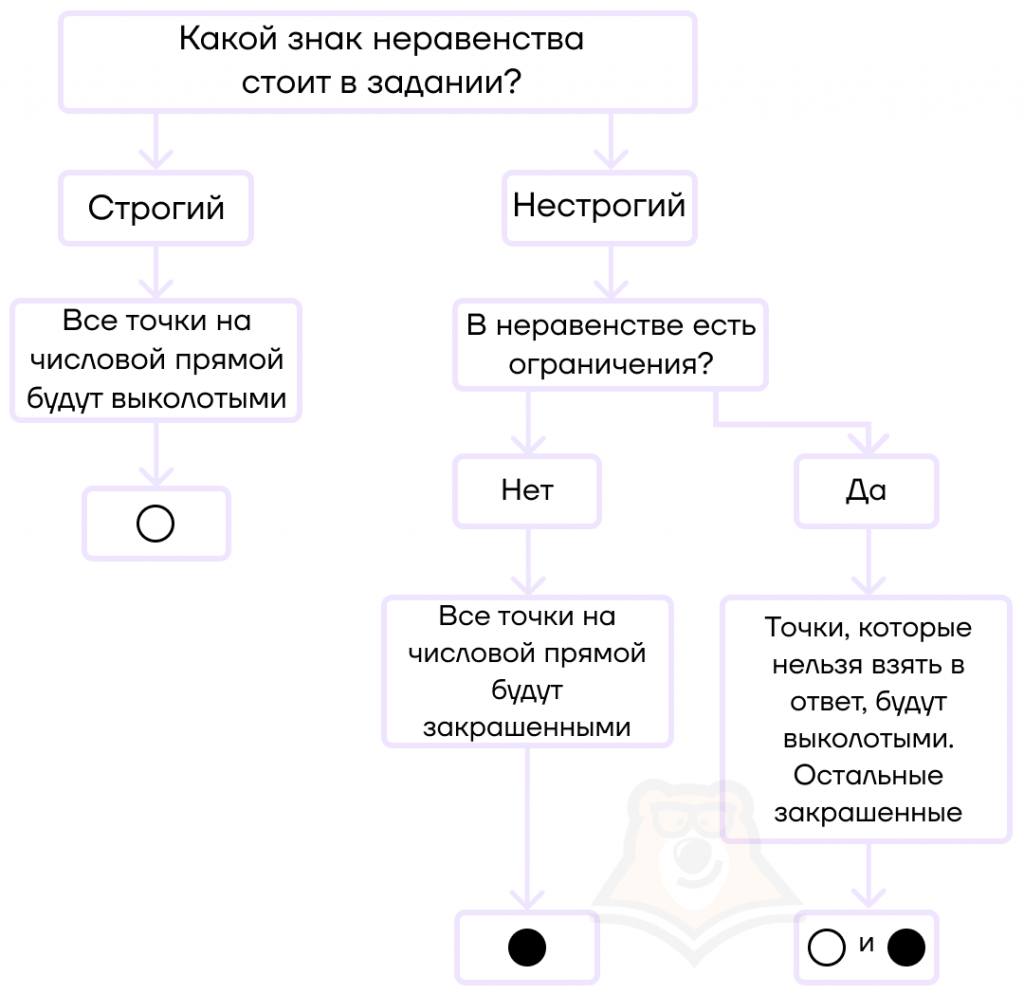
В случае сомнений мы всегда можем проверить себя по простой схеме.
Вывод:
— если знак неравенства строгий, то все точки будут выколотыми;
— если знак неравенства нестрогий, то точки будут закрашенными, кроме тех точек, которые нельзя взять в ответ (например, они не удовлетворяют ОДЗ).
Стоит отметить, что непрерывная функция будет менять знак только в точках, в которых она равна 0. Подробнее узнать про смену знака функции можно в статье «Определение и график функции». Именно поэтому в методе интервалов мы ищем и отмечаем нули функции на прямой — только при переходе через них будет меняться знак функции.
При этом существует способ, с помощью которого можно быстро расставить знаки на прямой. Достаточно определить знак на одном из интервалов, а дальше чередовать знаки при переходе через каждую точку на прямой.
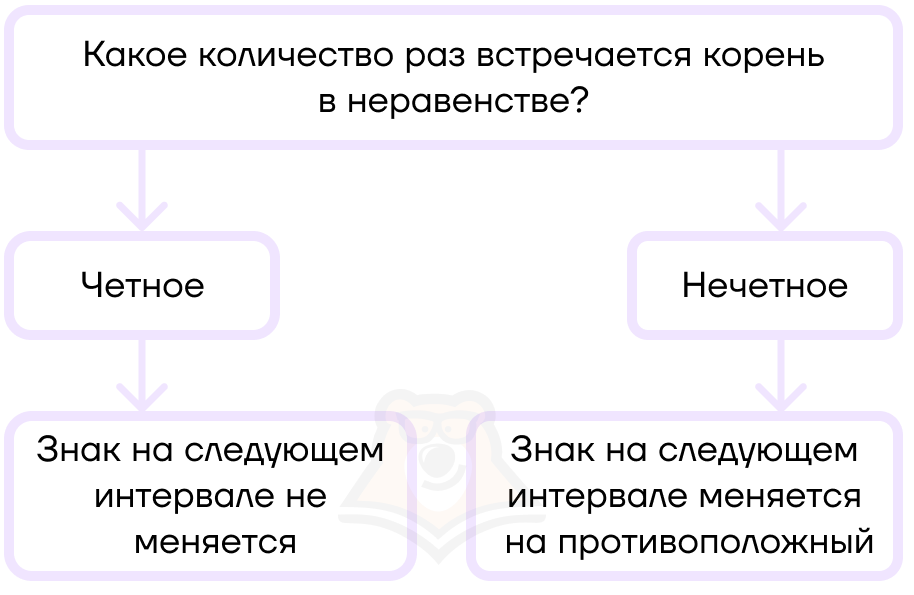
Правила чередования знаков:
- Если корень повторяется нечетное количество раз (то есть его степень нечетная), то знак при переходе на следующий интервал меняется.
- Если корень повторяется четное количество раз (его степень четная), то знак при переходе на следующий интервал не меняется.
Всегда будет нелишним перепроверить знак на каждом интервале, подставив значения в функцию, и убедиться в правильности расстановки знаков на прямой.
Но при расстановке можно пользоваться следующим алгоритмом, что значительно сократит время расстановки знаков.
Методом интервалов можно решить практически любое неравенство в задании 14 из ЕГЭ по профильной математике, также он может понадобиться в заданиях 8, 11 и 17 «профиля» или в задании 17 ЕГЭ по базовой математике.
На ОГЭ данным методом можно воспользоваться при решении неравенств из первой и второй частей — №13 и №20.
Так что осваивайте метод и 2 балла ЕГЭ или 3 балла ОГЭ будут у вас в кармане. Обязательно следуйте алгоритму решения неравенств методом интервалов, тогда вы точно решите неравенство верно.
Практика
Рассмотрим несколько примеров, чтобы на практике разобрать применение метода интервалов для решения неравенств.
Пример 1. Решить неравенство x2 + 8x — 33 > 0.
Шаг 1. Первым шагом необходимо найти нули функции, для этого приравниваем выражение слева к 0: x2 + 8x — 33 = 0.
Шаг 2. Находим корни уравнения, получаем х = 3 и х = -11.
Шаг 3. Расставляем полученные корни на числовой прямой. Поскольку знак неравенства строгий, то точки должны быть выколотыми:

Шаг 4. Дальше необходимо определить знаки на каждом интервале. Для этого подставим х = -12 в x2 + 8x — 33. Получаем:
(-12)2 + 8*(-12) — 33 = 144 — 96 — 33 = 15.
Получается положительное число, следовательно, интервал от минус бесконечности до -11 положительный. Поскольку все корни в неравенстве повторяются нечетное количество раз (по одному разу), то знаки чередуются.
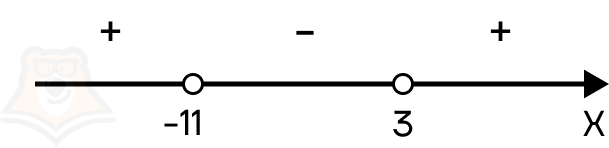
В ответ необходимо записать промежутки с положительным знаком, следовательно, ответом будет х ∈ (-∞; -11) U (3; +∞).
Пример 2. Решить неравенство (frac{2х^2 + 22х — 204}{(х-3)(х+5)} ≤ 0).
1. Находим нули функции.
Нули числителя: 2х2 + 22х — 204 = 0. Решая уравнение, получаем х = 6 и х = -17.
Нули знаменателя: (х — 3)(х + 5) = 0, следовательно, х = 3 и х = -5.
2. Расставляем полученные корни на числовой прямой. Нули числителя будут обозначены закрашенными точками, поскольку знак неравенства нестрогий. А вот нули знаменателя — выколотыми, поскольку знаменатель не может равняться 0, следовательно, и нули знаменателя не должны входить в итоговый промежуток.

3. Определяем знак на крайнем левом промежутке, подставляя х=-20 в дробь:
(frac{2(-20)^2 + 22(-20) — 204}{(-20 -3)(-20 +5)} = frac{2 * 400 — 440 — 204}{(-23) * (-15)} = 156345. )
Следовательно, промежуток положительный.
4. Поскольку каждый корень встречается один раз, то есть нечетное количество раз, то знаки будут чередоваться.

В ответ необходимо включить отрицательные промежутки. Следовательно, ответом будет х ∈ [-17; -5) U (3; 6].
Пример 3. Решить неравенство (frac{1}{х^2} ≥ frac{1}{х+2})
1. Первым делом следует отметить, что знаменатели не могут быть равны 0, следовательно, х2 ≠ 0 и х + 2 ≠ 0, отсюда получаем х ≠ 0 и х ≠ -2.
2. Теперь перенесем все части неравенства влево:
(frac{1}{х^2} — frac{1}{х+2} ≥ 0).
Приведем к общему знаменателю:
(frac{х + 2 — х^2}{х^2 (х + 2)} ≥ 0).
Для решения неравенства будет удобнее, если перед х2 в числителе будет стоять положительный знак, для этого умножим неравенство на -1.
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Получаем:
(frac{х^2 — х — 2}{х^2 (х + 2)} ≤ 0).
Теперь найдем нули функции.
Нули числителя: х2 — х — 2 = 0. Тогда х = -1 и х = 2.
Нули знаменателя: х = 0 и х = -2.
2. Расставим корни на числовой прямой, при этом нули числителя будут обозначены закрашенными точками, а нули знаменателя — выколотыми.

3. Определим знак на крайнем левом промежутке, подставив для этого х = -3 в дробь:
(frac{(-3)^2 — (-3) — 2}{(-3)^2 ((-3) + 2)} = frac{9 + 3 — 2}{9 * (-1)} = frac{10}{-9})
Промежуток отрицательный.
4. Дальше расставляем знаки, чередуя их. При этом следует заметить, что х = 0 — корень, повторяющийся четное количество раз (поскольку у х2 четная степень). Следовательно, при переходе через эту точку знак функции меняться не будет.

В ответ необходимо включить отрицательные промежутки, следовательно: х ∈ (-∞; -2) U [-1; 0) U (0; 2].
Давайте подведем итог. Для чего мы это изучили?
Конечно же, эти знания пригодятся на экзаменах, а также в решении школьных примеров с 8 класса по 11 класс.
Советуем после прочтения этой статьи попрактиковаться в рубрике «Проверь себя», чтобы закрепить полученные знания. После чего можете приступить к решению заданий посложнее, чтобы на экзамене у вас точно получилось решить подобные задания и набрать за них максимум баллов.
Фактчек
- Метод интервалов позволяет упростить решение любого неравенства, а также экономит время, которое ограничено на экзамене.
- Чтобы решить неравенство с помощью метода интервалов необходимо найти нули функции, расставить их на числовой прямой, а после определить знак каждого полученного интервала.
- Нули функции на прямой обозначаются точками, при этом закрашенные точки включают граничные значения в итоговый промежуток, а незакрашенные, напротив, исключают их из промежутка.
- Для определения знака на каждом интервале необходимо подставить любое значение из этого интервала в функцию.
- Для упрощения расстановки знаков можно пользоваться правилами чередования, определив знак только на одном интервале, а дальше менять знаки на каждом следующем. При этом если корень встречается в функции нечетное количество раз, то знак при переходе через эту точку на следующий интервал меняется, а если корень встречается четное количество раз, то знак на следующем интервале не меняется.
Проверь себя
Задание 1.
Какие знаки неравенства существуют?
- Строгие
- Нестрогие
- Строгие и нестрогие
- Больше и меньше
Задание 2.
Какой знак неравенства может встретиться в методе интервалов?
- Только больше или меньше.
- Только “больше или равно” или “меньше или равно”.
- Только “больше” и “больше или равно” или только “меньше” и “меньше или равно”.
- Любой.
Задание 3.
Какое утверждение верное?
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой закрашены.
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой выколоты.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой закрашены, даже если в неравенстве есть ограничения.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой выколоты.
Задание 4.
Какое утверждение верное?
- При переходе на числовой прямой на следующий интервал, знак на интервале всегда будет меняться.
- Если корень встречается в неравенстве четное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Если корень встречается в неравенстве нечетное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Невозможно определить правильное чередование знаков на прямой, не подставляя значение из каждого интервала в функцию.
Задание 5.
Если в неравенстве строгий знак неравенства, то какие скобочки могут встретиться в ответе?
- Круглые
- Квадратные
- И круглые, и квадратные
- Ни один из перечисленных вариантов
Ответы: 1. — 3 2. — 4 3. — 2 4. — 2 5. — 1
Метод интервалов: решение простейших строгих неравенств
12 ноября 2017
- Домашнее задание
- Ответы
Для начала — немного лирики, чтобы почувствовать проблему, которую решает метод интервалов. Допустим, нам надо решить вот такое неравенство:
(x − 5)(x + 3) > 0
Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 < 0 и x + 3 < 0. Таким образом, наше неравенство свелось к совокупности двух систем, которая, впрочем, легко решается:
Более продвинутые ученики вспомнят (может быть), что слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем:
x2 − 2x − 15 > 0
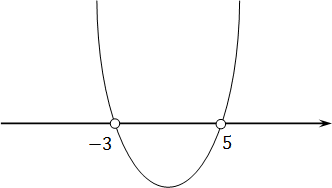
Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0. Попробуем нарисовать схему этой параболы:
Функция больше нуля там, где она проходит выше оси OX. В нашем случае это интервалы (−∞ −3) и (5; +∞) — это и есть ответ.
Обратите внимание: на рисунке изображена именно схема функции, а не ее график. Потому что для настоящего графика надо считать координаты, рассчитывать смещения и прочую хрень, которая нам сейчас совершенно ни к чему.
Почему эти методы неэффективны?
Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает — вы только вдумайтесь! — совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.
Это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4. Например:
(x − 7)(x − 1)(x + 4)(x + 9) < 0
Как решать такое неравенство? Перебирать все возможные комбинации плюсов и минусов? Да мы уснем быстрее, чем найдем решение. Рисовать график — тоже не вариант, поскольку непонятно, как ведет себя такая функция на координатной плоскости.
Для таких неравенств нужен специальный алгоритм решения, который мы сегодня и рассмотрим.
Что такое метод интервалов
Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) > 0 и f (x) < 0. Алгоритм состоит из 4 шагов:
- Решить уравнение f (x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
- Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
- Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней;
- Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется.
Вот и все! После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f (x) > 0, или знаком «−», если неравенство имеет вид f (x) < 0.
На первый взгляд может показаться, что метод интервалов — это какая-то жесть. Но на практике все будет очень просто. Стоит чуть-чуть потренироваться — и все станет понятно. Взгляните на примеры — и убедитесь в этом сами:
Задача. Решите неравенство:
(x − 2)(x + 7) < 0
Работаем по методу интервалов. Шаг 1: заменяем неравенство уравнением и решаем его:
(x − 2)(x + 7) = 0
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:
x − 2 = 0 ⇒ x = 2;
x + 7 = 0 ⇒ x = −7.
Получили два корня. Переходим к шагу 2: отмечаем эти корни на координатной прямой. Имеем:
Теперь шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000). Получим:
f (x) = (x − 2)(x + 7);
x = 3;
f (3) = (3 − 2)(3 + 7) = 1 · 10 = 10;
Получаем, что f(3) = 10 > 0, поэтому в самом правом интервале ставим знак плюс.
Переходим к последнему пункту — надо отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус.
Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси. Имеем:
Вернемся к исходному неравенству, которое имело вид:
(x − 2)(x + 7) < 0
Итак, функция должна быть меньше нуля. Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.
Задача. Решите неравенство:
(x + 9)(x − 3)(1 − x) < 0
Шаг 1: приравниваем левую часть к нулю:
(x + 9)(x − 3)(1 − x) = 0;
x + 9 = 0 ⇒ x = −9;
x − 3 = 0 ⇒ x = 3;
1 − x = 0 ⇒ x = 1.
Помните: произведение равно нулю, когда хотя бы один из множителей равен нулю. Именно поэтому мы вправе приравнять к нулю каждую отдельную скобку.
Шаг 2: отмечаем все корни на координатной прямой:
Шаг 3: выясняем знак самого правого промежутка. Берем любое число, которое больше, чем x = 1. Например, можно взять x = 10. Имеем:
f (x) = (x + 9)(x − 3)(1 − x);
x = 10;
f (10) = (10 + 9)(10 − 3)(1 − 10) = 19 · 7 · (−9) = − 1197;
f (10) = −1197 < 0.
Шаг 4: расставляем остальные знаки. Помним, что при переходе через каждый корень знак меняется. В итоге наша картинка будет выглядеть следующим образом:
Вот и все. Осталось лишь выписать ответ. Взгляните еще раз на исходное неравенство:
(x + 9)(x − 3)(1 − x) < 0
Это неравенство вида f (x) < 0, т.е. нас интересуют интервалы, отмеченные знаком минус. А именно:
x ∈ (−9; 1) ∪ (3; +∞)
Это и есть ответ.
Замечание по поводу знаков функции
Практика показывает, что наибольшие трудности в методе интервалов возникают на последних двух шагах, т.е. при расстановке знаков. Многие ученики начинают путаться: какие надо брать числа и где ставить знаки.
Чтобы окончательно разобраться в методе интервалов, рассмотрим два замечания, на которых он построен:
- Непрерывная функция меняет знак только в тех точках, где она равна нулю. Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f (x) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
- Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374, если нам захочется. Почему это важно? Да потому что многих учеников начинают грызть сомнения. Мол, что если для x = −4 мы получим плюс, а для x = 0 — минус? А ничего — такого никогда не будет. Все точки на одном интервале дают один и тот же знак. Помните об этом.
Вот и все, что нужно знать про метод интервалов. Конечно, мы разобрали его в самом простом варианте. Существуют более сложные неравенства — нестрогие, дробные и с повторяющимися корнями. Для них тоже можно применять метод интервалов, но это тема для отдельного большого урока.
Теперь хотел бы разобрать продвинутый прием, который резко упрощает метод интервалов. Точнее, упрощение затрагивает только третий шаг — вычисление знака на самом правом куске прямой. По каким-то причинам этот прием не проходят в школах (по крайней мере, мне никто такого не объяснял). А зря — ведь на самом деле этот алгоритм очень прост.
Итак, знак функции на правом куске числовой оси. Этот кусок имеет вид (a; +∞), где a — самый большой корень уравнения f (x) = 0. Чтобы не взрывать мозг, рассмотрим конкретный пример:
(x − 1)(2 + x)(7 − x) < 0;
f (x) = (x − 1)(2 + x)(7 − x);
(x − 1)(2 + x)(7 − x) = 0;
x − 1 = 0 ⇒ x = 1;
2 + x = 0 ⇒ x = −2;
7 − x = 0 ⇒ x = 7;
Мы получили 3 корня. Перечислим их в порядке возрастания: x = −2, x = 1 и x = 7. Очевидно, что наибольший корень — это x = 7.
Для тех, кому легче рассуждать графически, я отмечу эти корни на координатной прямой. Посмотрим, что получится:
Требуется найти знак функции f (x) на самом правом интервале, т.е. на (7; +∞). Но как мы уже отмечали, для определения знака можно взять любое число из этого интервала. Например, можно взять x = 8, x = 150 и т.д. А теперь — тот самый прием, который не проходят в школах: давайте в качестве числа возьмем бесконечность. Точнее, плюс бесконечность, т.е. +∞.
«Ты че, обкурился? Как можно подставить в функцию бесконечность?» — возможно, спросите вы. Но задумайтесь: нам ведь не нужно само значение функции, нам нужен только знак. Поэтому, например, значения f (x) = −1 и f (x) = −938 740 576 215 значат одно и то же: функция на данном интервале отрицательна. Поэтому все, что от вас требуется — найти знак, который возникает на бесконечности, а не значение функции.
На самом деле, подставлять бесконечность очень просто. Вернемся к нашей функции:
f (x) = (x − 1)(2 + x)(7 − x)
Представьте, что x — это очень большое число. Миллиард или даже триллион. Теперь посмотрим, что будет происходить в каждой скобке.
Первая скобка: (x − 1). Что будет, если из миллиарда вычесть единицу? Получится число, не особо отличающееся от миллиарда, и это число будет положительным. Аналогично со второй скобкой: (2 + x). Если к двойке прибавить миллиард, по получим миллиард с копейками — это положительное число. Наконец, третья скобка: (7 − x). Здесь будет минус миллиард, от которого «отгрызли» жалкий кусочек в виде семерки. Т.е. полученное число мало чем будет отличаться от минус миллиарда — оно будет отрицательным.
Осталось найти знак всего произведения. Поскольку в первых скобках у нас был плюс, а в последней — минус, получаем следующую конструкцию:
(+) · (+) · (−) = (−)
Итоговый знак — минус! И неважно, чему равно значение самой функции. Главное, что это значение — отрицательное, т.е. на самом правом интервале стоит знак минус. Осталось выполнить четвертый шаг метода интервалов: расставить все знаки. Имеем:
Исходное неравенство имело вид:
(x − 1)(2 + x)(7 − x) < 0
Следовательно, нас интересуют интервалы, отмеченные знаком минус. Выписываем ответ:
x ∈ (−2; 1) ∪ (7; +∞)
Вот и весь прием, который я хотел рассказать. В заключение — еще одно неравенство, которое решается методом интервалов с привлечением бесконечности. Чтобы визуально сократить решение, я не буду писать номера шагов и развернутые комментарии. Напишу только то, что действительно надо писать при решении реальных задач:
Задача. Решите неравенство:
x(2x + 8)(x − 3) > 0
Заменяем неравенство уравнением и решаем его:
x(2x + 8)(x − 3) = 0;
x = 0;
2x + 8 = 0 ⇒ x = −4;
x − 3 = 0 ⇒ x = 3.
Отмечаем все три корня на координатной прямой (сразу со знаками):
Справа на координатной оси стоит плюс, т.к. функция имеет вид:
f (x) = x(2x + 8)(x − 3)
А если подставить бесконечность (например, миллиард), получим три положительных скобки. Поскольку исходное выражение должно быть больше нуля, нас интересуют только плюсы. Осталось выписать ответ:
x ∈ (−4; 0) ∪ (3; +∞)
Смотрите также:
- Метод интервалов: случай нестрогих неравенств
- Тест по методу интервалов для строгих неравенств
- Сводный тест по задачам B12 (2 вариант)
- Профильный ЕГЭ-2022, задание 6. Геометрический смысл производной
- Формулы приведения: ускоряем вычисления в тригонометрии
- Задачи B4: перевозка груза тремя фирмами
Алгебра и начала математического анализа, 11 класс
Урок №15. Возрастание и убывание функции.
Перечень вопросов, рассматриваемых в теме
1) Нахождение промежутков монотонности функции,
2) Определение алгоритма нахождения промежутков возрастания и убывания функции,
3) Решение задачи на нахождения промежутков возрастания и убывания функции
Глоссарий по теме
Алгоритм нахождения промежутков возрастания и убывания функции y = f(x)
- Найти D(f)
- Найти f‘(x).
- Определить, при каких значениях хf‘(x) ≥ 0 (на этих промежутках функция возрастает); при каких значениях х f‘(x) ≤ 0 (на этих промежутках функция убывает))
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
1. Функция y = f(x), определенная на промежутке Х, называется возрастающей на этом промежутке, если для любой пары чисел х1 и х2 из этого промежутка из неравенства х1< х2 следует неравенство f(x1) <f(x2)
2. Функция y = f(x), определенная на промежутке Х, называется убывающей на этом промежутке, если для любой пары чисел х1 и х2 из этого промежутка из неравенства х1< х2 следует неравенство f(x1) >f(x2)
Теоремы
- Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≥ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек),то функция y = f(x) возрастает на промежутке Х.
- Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≤ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек),то функция y = f(x) убывает на промежутке Х.
Примеры и разбор решения заданий тренировочного модуля
№1. Определите промежутки монотонности функции
у = -3х3 + 4х2 + х – 10.
Решение
1.Найдем область определения функции.
D(y) =
2.Найдем производную функции.
y’ = (x – 1)(-9x – 1)
3.Определим, на каких промежутках производная положительна (на этих промежутках функция возрастает), на каких – отрицательна (на этих промежутках функция убывает).
Применим для этого метод интервалов. Для определения знака на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Так как на интервале 
Так как на интервале 
Так как на интервале 
Так как в точках 
Следовательно, функция возрастает на 


Ответ: Функция возрастает на
Функция убывает на 

№2. Определите промежутки монотонности функции
у = х5–5х4 +5х3 – 4.
Решение:
y‘ =
- Функция возрастает на
; функция убывает на
.
Ответ: Функция возрастает на 
функция убывает на 


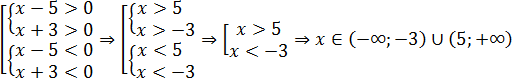







 ; функция убывает на
; функция убывает на  .
.