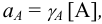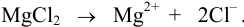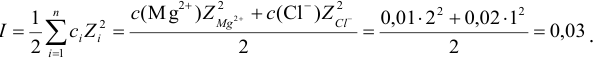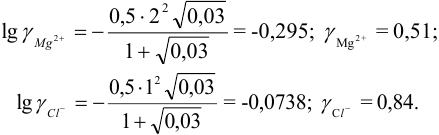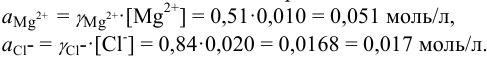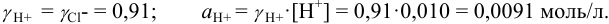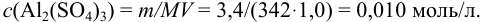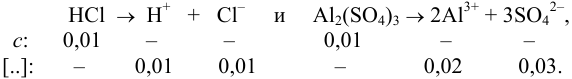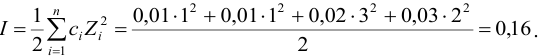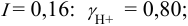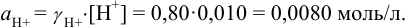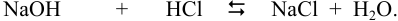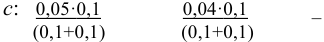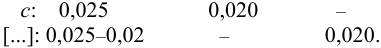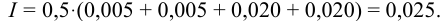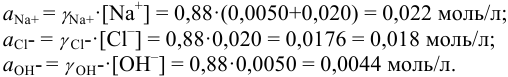Равновесия в растворах
Чтобы не усложнять термодинамические
соотношения, выведенные для идеальных
растворов, Льюис предложил использовать
в термодинамических соотношениях вместо
концентрации активность.
Активность компонента связана с его
концентрацией в растворе через коэффициент
активности :.
Для растворов электролитов коэффициент
активности связан с величиной ионной
ассоциации. Чем сильнее ионная ассоциация
в растворе, тем ниже коэффициент
активности. Ионная ассоциация усиливается
с ростом концентрации электролита в
растворе и с увеличением заряда ионов.
Если между ионами нет химического
взаимодействия, то степень ассоциации
ионов определяется ионной силой раствора.
Ионной силой называют полусумму
произведений моляльных концентраций
всех ионов в растворе на квадраты их
зарядов:
.
(1.1)
Чем выше ионная сила раствора, тем ниже
коэффициент активности. При этом в
растворах с одинаковой ионной силой
среднеионные коэффициенты активности
в первом приближении совпадают. В
предельно разбавленном растворе ионная
ассоциация отсутствует и коэффициент
активности равен единице, т.е. активность
равна концентрации.
В рамках теории Дебая-Хюккеля для расчета
среднеионного коэффициента активности
вещества в водном растворе применяется
одно из двух уравнений:
(1.2)
при ионной силе раствора менее 0,05 моль/кг
и
(1.3)
при ионной силе раствора от 0,05 до
0,5 моль/кг, где
и
– заряд катиона и аниона.
Теория Дебая-Хюккеля предполагает
возможность расчета коэффициента
активности отдельного иона по уравнениям
(1.4)
при ионной силе раствора менее 0,05 моль/кг
и
(1.5)
при ионной силе раствора от 0,05 до
0,5 моль/кг, где
– заряд отдельного иона.
Примеры решения задач Пример 1.
Вычислить ионную силу раствора сульфата
натрия концентрацией 0,1 моль/кг и его
среднеионный коэффициент активности.
Решение.1. Составить уравнение
диссоциации соли:
.
2. Согласно уравнению диссоциации
концентрация катионов натрия
,
концентрация сульфат-ионов.
3. Вычислить ионную силу раствора:
4. Вычислить среднеионный коэффициент
активности сульфата натрия:
.
Задачи для решения
1. – 60. Вычислить ионную силу раствора
заданной концентрации.
|
№ |
Вещество |
Концентрация |
d, |
|
1 |
Al2(SO4)3 |
0,15 экв/л |
1,009 |
|
2 |
AlCl3 |
0,55 % |
1,007 |
|
3 |
Al(NO3)3 |
5,47 |
1,01 |
|
4 |
Al2(SO4)3 |
0,9 |
1,009 |
|
5 |
Al(NO3)3 |
1,05 % |
1,01 |
|
6 |
BaCl2 |
1,69 моль/л |
1,28 |
|
7 |
Ba(NO3)2 |
0,525моль/л |
1,092 |
|
8 |
CaCl2 |
2,2 % |
1,01 |
|
9 |
Ca(NO3)2 |
2% |
1,01 |
|
10 |
CdCl2 |
0,5 |
1,08 |
|
11 |
Cd(NO3)2 |
0,5 |
1,04 |
|
12 |
CrCl3 |
0,6 |
1,022 |
|
13 |
Cr2(SO4)3 |
0,3 |
1,021 |
|
14 |
Cr(NO3)3 |
3% |
1,02 |
|
15 |
CuSO4 |
1,037 |
1,206 |
|
16 |
CuCl2 |
0,04 |
1,009 |
|
17 |
Cu(NO3)2 |
1,037 |
1,20 |
|
18 |
FeCl3 |
1,9 моль/л |
1,234 |
|
19 |
FeSO4 |
0,3 экв/л |
1,02 |
|
20 |
Fe2(SO4)3 |
0,3 моль/л |
1,03 |
|
21 |
Fe(NO3)3 |
0,3 % |
1,0 |
|
22 |
H2SO4 |
1,56 |
1,095 |
|
23 |
H2SO4 |
3,4 |
1,109 |
|
24 |
H2SO4 |
5,9 |
1,18 |
|
25 |
H3PO4 |
2,79 моль/л |
1,115 |
|
26 |
H3PO4 |
7,3 |
1,181 |
|
27 |
H3PO4 |
3 мол. |
1,08 |
|
28 |
HCl |
0,4 мол. % |
1,002 |
|
29 |
HCl |
1,17 |
1,05 |
|
30 |
HCl |
2% |
1,01 |
|
31 |
HCl |
17,4 |
1,149 |
|
32 |
Hg(NO3)2 |
0,25 |
1,174 |
|
33 |
HNO3 |
5,1 |
1,03 |
|
34 |
HNO3 |
6 |
1,01 |
|
35 |
K2Cr2O7 |
0,18 |
1,033 |
|
36 |
KMnO4 |
0,25 экв/л |
1,027 |
|
37 |
KOH |
3 мол. % |
1,073 |
|
38 |
KOH |
34 |
1,336 |
|
39 |
KOH |
6,3 |
1,147 |
|
40 |
KOH |
8,107 |
1,336 |
|
41 |
KOH |
0,12 моль/кг |
1,0 |
|
42 |
MgSO4 |
20 |
1,219 |
|
43 |
MgCl2 |
2 |
1,02 |
|
44 |
Mg(NO3)2 |
0,05 моль/л |
1,01 |
|
45 |
MnCl2 |
10 |
1,086 |
|
46 |
MnSO4 |
1 |
1,0 |
|
47 |
Na2CO3 |
0,39 моль/л |
1,019 |
|
48 |
Na2CO3 |
4,1 % |
1,019 |
|
49 |
NaBr |
5,8 мол. % |
1,21 |
|
50 |
NaBr |
26 % |
1,21 |
|
51 |
NaCl |
7,1 мол. % |
1,147 |
|
52 |
NaCl |
15 % |
1,109 |
|
53 |
NaCl |
4,5% |
1,03 |
|
54 |
NaOH |
13 % |
1,142 |
|
55 |
NaOH |
1,3 % |
1,042 |
|
56 |
NaOH |
1,48 г/л |
1,0 |
|
57 |
NaOH |
0,37 экв/л |
1,142 |
|
58 |
Pb(NO3)2 |
30 % |
1,328 |
|
59 |
ZnSO4 |
1,374 экв/л |
1,107 |
|
60 |
ZnSO4 |
87 г/л |
1,084 |
61. Для осаждения в виде хлорида всего
серебра, содержащегося в 100 мл раствора
нитрата серебра, потребовалось 50 мл
0,2 н. раствора соляной кислоты. Какова
нормальность раствора нитрата серебра,
какая масса хлорида серебра выпала в
осадок? Найти ионную силу конечного
раствора.
62. На нейтрализацию 31 мл 0,16 н.
раствора щелочи требуется 217 мл
раствора серной кислоты. Чему равна
нормальность раствора серной кислоты?
Найти ионную силу раствора после смешения
кислоты и щелочи.
63. Какой объем 0,3 н. раствора серной
кислоты требуется для нейтрализации
раствора содержащего 0,32 г гидроксида
натрия в 40 мл? Найти ионную силу
раствора после реакции.
64. На нейтрализацию одного литра
раствора, содержащего 1,4 г гидроксида
калия, требуется 50 мл раствора
фосфорной кислоты. Вычислить нормальность
раствора кислоты и ионную силу.
65. Какая масса азотной кислоты
содержалась в 0,5 л раствора, если на
нейтрализацию его потребовалось 35 мл
0,4 н. раствора гидроксида натрия?
Вычислить ионную силу раствора после
нейтрализации.
66. Сколько миллилитров 1 н. раствора
едкого натра потребуется для полной
нейтрализации 300 мл 0,1 М раствора
серной кислоты? Вычислить ионную силу
раствора после нейтрализации.
67. Сколько миллилитров 0,1 н. едкого
натра (NaOH) потребуется для осаждения
меди в виде гидроксида из 20 мл раствора
сульфата меди, в 1 л которого содержится
10 г меди? Вычислить ионную силу
раствора после реакции.
68. Сколько миллилитров 10 % соляной
кислоты плотностью 1,047 г/ см3потребуется для нейтрализации раствора,
содержащего 8,5 г гидроксида бария?
Вычислить ионную силу раствора после
реакции.
69. Сколько миллилитров раствора соды,
содержащего в 1 л 21,2 г соли, надо
добавить к 30 мл 0,2 н. раствора
хлорида кальция для полного осаждения
кальция в виде карбоната? Вычислить
ионную силу раствора после реакции.
70. Сколько граммов гидроксида железа
выпадет в осадок, если к 500 мл 0,2 н.
раствора хлорида железа (III) (плотность
1,03 г/см3) добавить 5 г гидроксида
натрия? Вычислить ионную силу раствора
после реакции.
71. В каком объемном отношении надо
смешать растворы гидроксида бария с
концентрацией 95,5 г/л и 0,5 н. соляной
кислоты для получения раствора с
нейтральной средой? Вычислить ионную
силу раствора после реакции.
72. На нейтрализацию 20 мл раствора
едкого кали потребовалось 13 мл 0,2 н.
раствора соляной кислоты. Сколько
граммов едкого кали содержится в 1 л
раствора? Вычислить ионную силу раствора
после реакции.
73. Сколько миллилитров раствора
нитрата серебра, содержащего 5 г/л
серебра, надо добавить к 10 мл 0,2 н.
раствора хлорида натрия, чтобы полностью
удалить из раствора ионы хлора? Вычислить
ионную силу раствора после реакции.
74. Сколько миллилитров 2 н. серной
кислоты потребуется для превращения
1,56 г гидроксида алюминия в сульфат
алюминия? Вычислить ионную силу раствора
после реакции.
75. Сколько граммов карбоната кальция
можно растворить в 100 мл 20 % соляной
кислоты плотностью 1,1 г/см3?
Вычислить объем, который займет
выделившийся газ при нормальных условиях
и ионную силу полученного раствора.
76. К 5 г цинка прибавили 100 мл
10,2 % соляной кислоты (плотность
раствора 1,05 г/см3). Какое вещество,
и в каком количестве осталось в избытке?
Вычислить объем выделившегося водорода
при 20ºС и 750 мм рт. ст. и ионную
силу полученного раствора.
77. На нейтрализацию 20 мл 5,66 %
раствора гидроксида калия плотностью
1,053 г/см3пошло 12,1 мл раствора
серной кислоты плотностью 1,052 г/см3.
Определить концентрацию (%) раствора
серной кислоты и ионную силу конечного
раствора.
78. Какое количество миллилитров
0,5 н. раствора сульфата натрия надо
прилить к 100 мл 16 % раствора хлорида
бария плотностью 1,156 г/см3, чтобы
полностью осадить сульфат-ион? Определить
ионную силу конечного раствора.
79. На нейтрализацию 50 мл раствора
фосфорной кислоты плотностью 1,01 г/см3израсходовано 31,2 г 1 н. раствора
гидроксида натрия плотностью 1,04 г/см3.
Определить концентрацию (%) фосфорной
кислоты и ионную силу конечного раствора.
80. 10 г сплава меди с цинком обработали
соляной кислотой (объем раствора 1,5 л,
концентрация 0,02 н.). При этом выделилось
570 мл водорода, измеренных при
температуре 27ºС и давлении 1 атм.
Определить состав сплава и выразить
его в массовых и мольных долях. Вычислить
ионную силу раствора после реакции.
81. При растворении 15 г сплава
серебра с алюминием раствором едкого
натра объемом 0,5 л и концентрацией
1,25 г/л выделилось 13 мл водорода
измеренного при температуре 57ºС и
давлении 15105Па.
Определить состав сплава и выразить
его в массовых и мольных долях. Вычислить
ионную силу раствора после реакции.
82. Растворили в 100 мл 0,05 н. азотной
кислоты 5 г сплава меди и золота. При
этом выделилось 0,99 мл оксида азота (II),
измеренных при температуре 37ºС и давлении
1,2105Па.
Определить состав сплава и выразить
его в массовых и мольных долях. Вычислить
ионную силу раствора после реакции.
83. Для нейтрализации 20 мл 0,1 н.
раствора соляной кислоты потребовалось
8 мл раствора гидроксида натрия.
Сколько граммов NaOH содержит 1 л этого
раствора? Вычислить ионную силу раствора
после реакции.
84. Какой объем 0,2 н. раствора кислоты
требуется для нейтрализации раствора,
содержащего 0,51 г гидроксида калия в
30 мл? Вычислить ионную силу раствора
после реакции.
85. Сколько и какого вещества останется
в избытке, если к 150 мл 0,4 н. раствора
соляной кислоты прибавить 250 мл 0,2 н.
раствора гидроксида натрия? Вычислить
ионную силу раствора после реакции.
86. Определить эквивалентную массу
кислоты, если на нейтрализацию раствора,
содержащего 0,63 г
кислоты, израсходовано 20 мл
0,5 н. раствора щелочи. Вычислить ионную
силу раствора щелочи.
87. На нейтрализацию раствора,
содержащего 4,05 г кислоты, израсходовано
40 мл раствора едкого натра (NaOH)
концентрацией 10 % плотностью
1,109 г/см3. Определить эквивалентную
массу кислоты. Вычислить ионную силу
раствора щелочи.
88. К 50 л раствора фосфорной кислоты
концентрацией 8 % плотностью 1,042 г/см3прибавили 2 л фосфата натрия
концентрацией 5 г/л. Рассчитать
молярную концентрацию фосфат-иона в
полученном растворе и его ионную силу.
89. На нейтрализацию 10 мл раствора
серной кислоты концентрацией 22 %
плотностью 1,155 г/см3потребовалось
50 мл раствора щелочи концентрацией
41,6 г/л. Определить из этих данных
эквивалентную массу щелочи и ионную
силу конечного раствора.
90. Смешали 4 мл серной кислоты
концентрацией 40 % (плотность 1,303 г/см3)
и 200 мл серной кислоты, концентрацией
0,001 моль/л. Рассчитать нормальную
концентрацию и ионную силу полученного
раствора.
91. Смешали 8 л раствора соляной
кислоты концентрацией 4 моль/л и 11 л
раствора ее же концентрацией 2 г/л.
Рассчитать концентрацию полученного
раствора (г/л) и его ионную силу .
92. К 1,2 л 1,8 н. раствора сульфата
хрома (III) добавили 3 л
1 % раствора гидроксида аммония
(плотность равна 1 г/см3).
Рассчитать ионную силу полученного
раствора.
93. К раствору объемом 30 мл, содержащему
10 г серной кислоты в 100 мл раствора,
прибавили 40 мл раствора NaOH, содержащего
9 г гидроксида натрия в 100 мл
раствора. Найти молярную концентрацию
того вещества, которое останется в
избытке и ионную силу полученного
раствора.
94. Смешали раствор нитрата серебра,
концентрацией 1 % плотностью 1,01 г/см3и раствор соляной кислоты концентрацией
5 % (плотность 1,02 г/см3) в
соотношении 3:4. Рассчитать молярную
концентрацию нитрат-иона в полученном
растворе и ионную силу полученного
раствора.
95. Какой объем раствора серной кислоты
концентрацией 10 % (плотность 1,07 г/см3)
потребуется для полной нейтрализации
0,5 л раствора NaOH концентрацией 16 г/л?
Вычислить ионную силу конечного раствора.
96. Смешали 10 мл раствора HCl
концентрацией 10 % (плотность 1,047 г/см3)
и 10 мл раствора HCl концентрацией 6 %
(плотность 1,028 г/см3). Рассчитать
массовую долю и молярную концентрацию
соляной кислоты в полученном растворе
и его ионную силу.
97. Из раствора нитрата серебра
концентрацией 2 % (плотность 1,015 г/см3)
по реакции с хлоридом натрия образуется
14,35 г. хлорида серебра. Вычислить
исходный объем раствора нитрата серебра
и ионную силу конечного раствора.
98. Сколько миллилитров 0,5 н. раствора
сульфата натрия нужно прилить к 100 мл
раствора хлорида бария концентрацией
16 % (плотность 1,156 г/см3), чтобы
полностью осадить сульфат-ионы? Найти
ионную силу конечного раствора.
99. Металл вытеснил из 100 мл соляной
кислоты 348 мл водорода, измеренного
при 20°С и 99,5 кПа. Рассчитать нормальную
концентрацию хлорида металла в полученном
растворе и его ионную силу.
100. К 30 мл горячего 10 %-ного водного
раствора сульфата алюминия (плотность
1,1 г/см3) прилили 20 мл горячего
10 %-ного водного раствора карбоната
натрия (плотность 1,15 г/см3).
Смесь оставили на сутки на воздухе.
Определить ионную силу конечного
раствора.
101. К 20 мл горячего 20 %-ного водного
раствора хлорида хрома (плотность
1,1 г/см3) прилили 20 мл горячего
10 %-ного водного раствора сульфида
натрия (плотность 1,15 г/см3).
Смесь оставили на сутки. Определите
ионную силу конечного раствора.
102. К 20 мл горячего 20 %-ного водного
раствора хлорида железа (III)
(плотность 1,2 г/см3) прилили
15 мл горячего 20 %-ного водного
раствора силиката натрия (плотность
1,2 г/см3). Смесь оставили на сутки
на воздухе. Определите ионную силу
конечного раствора.
103. К 40 мл горячего 10 %-ного водного
раствора сульфата хрома (III)
(плотность 1,1 г/см3) прилили
10 мл горячего 20 %-ного водного
раствора карбоната натрия (плотность
1,2 г/см3). Смесь оставили на сутки
на воздухе. Определите ионную силу
конечного раствора.
104. К 25 мл горячего 10 %-ного водного
раствора сульфата железа (III)
(плотность 1,1 г/см3) прилили
20 мл горячего 20 %-ного водного
раствора карбоната натрия (плотность
1,2 г/см3). Смесь оставили на сутки
на воздухе. Определите ионную силу
конечного раствора.
105. К 30 мл горячего 10 %-ного водного
раствора сульфата алюминия (плотность
1,1 г/см3) прилили 20 мл горячего
10 %-ного водного раствора сульфида
натрия (плотность 1,15 г/см3).
Смесь оставили на сутки на воздухе.
Определите ионную силу конечного
раствора.
106. К 20 мл горячего 20 %-ного водного
раствора хлорида хрома (III)
(плотность 1,1 г/см3) прилили
20 мл горячего 10 %-ного водного
раствора карбоната натрия (плотность
1,15 г/см3). Смесь оставили на
сутки на воздухе. Определите ионную
силу конечного раствора.
107. К 20 мл горячего 20 %-ного водного
раствора хлорида хрома (III)
(плотность 1,1 г/см3) прилили
20 мл горячего 10 %-ного водного
раствора силиката натрия (плотность
1,2 г/см3). Смесь оставили на сутки
на воздухе. Определите ионную силу
конечного раствора.
108. К 20 мл горячего 20 %-ного водного
раствора хлорида железа (III)
(плотность 1,2 г/см3) прилили
20 мл горячего 10 %-ного водного
раствора сульфида натрия (плотность
1,15 г/см3). Смесь оставили на
сутки на воздухе. Определите ионную
силу конечного раствора.
109. К 40 мл горячего 10 %-ного водного
раствора сульфата алюминия (плотность
1,1 г/см3) прилили 20 мл горячего
20 %-ного водного раствора силиката
натрия (плотность 1,2 г/см3). Смесь
оставили на сутки на воздухе. Определите
ионную силу конечного раствора.
110. В раствор, содержащий нитрат калия,
нитрат серебра и нитрат меди (II)
массой 250 г поместили железные опилки,
массой 1,25 г. Какие металлы и в каком
количестве выделятся из раствора, если
содержание солей металлов в исходном
растворе следующее: нитрат калия 0,5 %,
нитрат меди 0,94 %, нитрат серебра
1,021 %? Вычислить ионную силу конечного
раствора.
111. К 20 мл 0,1 М раствора нитрата
свинца (II) прилили 20 мл
0,15 н. раствора иодида калия. Найти
массу образовавшегося осадка и вычислить
ионную силу конечного раствора.
112. К 200 мл раствора, содержащего
0,3 г сульфида калия прибавили 300 мл
0,1 % раствора серной кислоты (плотность
– 1,0 г/см3). Найти объем
выделившегося газа (Т= 25°С,Р=
1 атм.) и ионную силу конечного раствора.
113. Смешали 200 мл 4 % раствора
сульфата меди (II)
(плотность 1,04 г/см3) и 400 мл
1 % раствора гидроксида натрия
(плотностью 1 г/см3). Определить
массу осада и ионную силу конечного
раствора.
114. 5 г карбоната кальция растворили
в 150 мл 4 % соляной кислоты (плотность
1,02 г/см3). Найти объем выделившегося
углекислого газа и ионную силу конечного
раствора.
115. Смешали 200 мл 0,1 н. раствора
бромида алюминия и 120 мл 0,15 н.
раствора нитрата серебра. Определить
ионную силу конечного раствора и массу
образовавшегося осадка.
116. К 5 г судбфида натрия прилили
500 мл 0,1 н. раствора серной кислоты.
Определить объем сероводорода и ионную
силу конечного раствора.
117. К 50 мл 1,5 % раствора гидроксида
бария (плотность 1,008 г/см3)
прилили 300 мл 2 % раствора соляной
кислоты (плотность 1,01 г/см3).
Вычислить ионную силу конечного раствора.
118. 1,546 г гидроксида железа (III)
растворили в 300 мл азотной кислоты,
концентрацией 10,5 г/л. Определить
концентрацию нитрата железа (III)
в полученом растворе и ионную силу этого
раствора.
119. Смешали растворы хлорида железа (III)
и гидроксида калия в объемном соотношении
1:1 (по 2 литра) и одинаковой концентрацией
1 г/л. Определить ионную силу полученного
раствора.
120. К 150 мл 0,1 н. нитрата бария
прилили 100 мл 0,1 н. раствора сульфата
натрия. Определить массу сульфата бария
и ионную силу получившегося раствора.
From Wikipedia, the free encyclopedia
The ionic strength of a solution is a measure of the concentration of ions in that solution. Ionic compounds, when dissolved in water, dissociate into ions. The total electrolyte concentration in solution will affect important properties such as the dissociation constant or the solubility of different salts. One of the main characteristics of a solution with dissolved ions is the ionic strength. Ionic strength can be molar (mol/L solution) or molal (mol/kg solvent) and to avoid confusion the units should be stated explicitly.[1] The concept of ionic strength was first introduced by Lewis and Randall in 1921 while describing the activity coefficients of strong electrolytes.[2]
Quantifying ionic strength[edit]
The molar ionic strength, I, of a solution is a function of the concentration of all ions present in that solution.[3]
where one half is because we are including both cations and anions, ci is the molar concentration of ion i (M, mol/L), zi is the charge number of that ion, and the sum is taken over all ions in the solution. For a 1:1 electrolyte such as sodium chloride, where each ion is singly-charged, the ionic strength is equal to the concentration. For the electrolyte MgSO4, however, each ion is doubly-charged, leading to an ionic strength that is four times higher than an equivalent concentration of sodium chloride:
Generally multivalent ions contribute strongly to the ionic strength.
Calculation example[edit]
As a more complex example, the ionic strength of a mixed solution 0.050 M in Na2SO4 and 0.020 M in KCl is:
Non-ideal solutions[edit]
Because in non-ideal solutions volumes are no longer strictly additive it is often preferable to work with molality b (mol/kg of H2O) rather than molarity c (mol/L). In that case, molal ionic strength is defined as:
in which
- i = ion identification number
- z = charge of ion
- b = molality (mol solute per Kg solvent)[4]
Importance[edit]
The ionic strength plays a central role in the Debye–Hückel theory that describes the strong deviations from ideality typically encountered in ionic solutions.[5][6] It is also important for the theory of double layer and related electrokinetic phenomena and electroacoustic phenomena in colloids and other heterogeneous systems. That is, the Debye length, which is the inverse of the Debye parameter (κ), is inversely proportional to the square root of the ionic strength. Both molar and molal ionic strength have been used, often without explicit definition. Debye length is characteristic of the double layer thickness. Increasing the concentration or valence of the counterions compresses the double layer and increases the electrical potential gradient.
Media of high ionic strength are used in stability constant determination in order to minimize changes, during a titration, in the activity quotient of solutes at lower concentrations. Natural waters such as mineral water and seawater have often a non-negligible ionic strength due to the presence of dissolved salts which significantly affects their properties.
See also[edit]
- Activity (chemistry)
- Activity coefficient
- Bromley equation
- Davies equation
- Debye–Hückel equation
- Debye–Hückel theory
- Double layer (interfacial)
- Double layer (electrode)
- Double layer forces
- Electrical double layer
- Gouy-Chapman model
- Flocculation
- Peptization (the inverse of flocculation)
- DLVO theory (from Derjaguin, Landau, Verwey and Overbeek)
- Interface and colloid science
- Osmotic coefficient
- Pitzer equations
- Poisson–Boltzmann equation
- Specific ion Interaction Theory
- Salting in
- Salting out
External links[edit]
- Ionic strength
- Ionic strength introduction at the EPA web site
References[edit]
- ^ Solomon, Theodros (2001). «The definition and unit of ionic strength». Journal of Chemical Education. 78 (12): 1691. Bibcode:2001JChEd..78.1691S. doi:10.1021/ed078p1691.
- ^ Sastre de Vicente, Manuel E. (2004). «The concept of ionic strength eighty years after its introduction in chemistry». Journal of Chemical Education. 81 (5): 750. Bibcode:2004JChEd..81..750S. doi:10.1021/ed081p750.
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the «Gold Book») (1997). Online corrected version: (2006–) «Ionic strength, I«. doi:10.1351/goldbook.I03180
- ^ Standard definition of molality
- ^ Debye, P.; Huckel, E. (1923). «Zur Theorie der Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinungen» [The theory of electrolytes. I. Lowering of freezing point and related phenomena] (PDF). Physikalische Zeitschrift. 24: 185–206. Archived from the original (PDF) on 2013-11-02.
- ^ Skoog, D.A.; West, D.M.; Holler, F.J.; Crouch, S.R. (2004). Fundamentals of analytical chemistry. Brooks/Cole Pub Co. ISBN 0-03-058459-0.
Влияние электростатических взаимодействий на поведение ионов в растворе. Ионная сила раствора. Коэффициент активности
Характеристикой электростатического поля в растворе и мерой электростатических взаимодействий ионов является ионная сила раствора I, связанная с концентрацией ионов 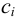
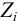
Ионной силой раствора определяется коэффициент активности иона 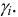
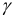
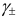
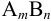
Например, для 0,01 М раствора 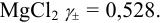
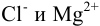
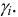
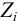
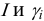
В практических расчетах для оценки коэффициентов активности используют ряд постулатов, упрощающих расчеты:
- Коэффициенты активности ионов равного заряда, независимо от знака и размера, приблизительно равны.
- Растворы, содержащие только нейтральные молекулы, можно считать идеальными
.
- Разбавленные растворы электролитов (особенно — слабых!) приближаются к идеальным
.
Поэтому при расчете величины 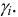
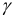
Коэффициент активности является мерой отклонения реальной системы от идеальной. Он связывает концентрацию иона и его активность 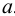
где [А] — равновесная концентрация иона А. Активность имеет размерность концентрации (моль/л).
Следует помнить, что при расчетах любого из четырех видов химических равновесий с применением табличных (термодинамических) констант равновесия получают значения активностей частиц, а не их равновесные концентрации. Расчет равновесных концентраций при I > 0 проводится с учетом у с использованием уравнения (2.11), связывающего различные константы.
Пример 2.1.
Вычислить ионную силу, коэффициенты активности и активность ионов в 0,010 М растворе 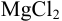
Решение:
Уравнение диссоциации сильного электролита
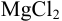
Начальная концентрация (моль/л) с: 0,010
Равновесные концентрации (моль/л) […]: — 0,010 0,020.
По формуле (2.1) вычисляют ионную силу раствора:
Коэффициенты активности можно найти в табл. 1 приложения: при / = 0,03 для двухзарядного иона 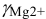
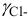
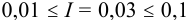
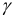
Активности ионов соответственно равны:
Пример 2.2.
Во сколько раз изменится активность ионов водорода в 0,010М растворе 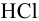
Решение:
Для 0,010 М раствора 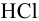
Молярная концентрация раствора 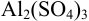
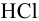
В полученном растворе сильных электролитов устанавливаются равновесия:
В величину I (формула 2.1) вносят вклад все ионы, находящиеся в растворе:
При
Отношение полученных активностей (0,0091/0,0080) показывает, что при введении в раствор 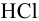
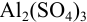
Пример 2.3.
Вычислить ионную силу и активности ионов в растворе, полученном при сливании по 100 мл 0,050 М раствора 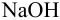
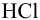
Решение:
При сливании растворов протекает реакция нейтрализации с образованием достаточно слабого электролита — воды, диссоциацией которой пренебрегаем. Данные указывают на избыток взятой щелочи.
С учетом разбавления
и после расчета
В растворе присутствуют ионы 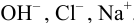
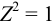
Соответственно 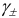
Проверкой решения может быть выполнение принципа электронейтральности раствора в целом:
Эти примеры взяты со страницы примеров решения задач по аналитической химии:
Решение задач по аналитической химии
Возможны вам будут полезны эти страницы:
Ионная сила раствора
Ульяна Власова
Эксперт по предмету «Химия»
Задать вопрос автору статьи
Понятие ионной силы и формула ее расчета
Определение 1
Ионная сила раствора (I) — это мера интенсивности электрического поля, создаваемого ионами в растворе.
Ионная сила представляет собой полусумму произведений концентрации каждого иона на квадрат его заряда.
$mathrm {I = frac {1}{2} sumlimits_{i=1}^n С_iZ_i^{2}}$
Здесь:
- $mathrm {С_i}$ — концентрация ионов,
- $mathrm {Z_i}$ — заряд ионов
Закон ионной силы и коэффициент активности иона
Опытным путём был установлен закон ионной силы Льюиса и Рендела. Он заключается в том, что коэффициент активности электролита, а следовательно, и коэффициенты активности его ионов зависят от ионной силы, но не зависят от вида остальных ионов в данном растворе.
То есть ионная сила определяет коэффициент активности иона $mathrm {gamma_i}$. Пользуются средним коэффициентом активности, так как величину активности индивидуального иона определить невозможно.
$mathrm {gamma_{pm}^{m+n} = gamma_A^{m} cdot gamma_B^{n}}$
Рассмотрим некоторые эмпирические уравнения для расчета коэффициентов активности:
-
Закон Дебая-Хюккеля:
$mathrm {lggamma_i = -0,5Z_i^{2}sqrt{I}}$ при $mathrm {I leq 0,01 ммоль/л}$
-
Расширенное уравнение Дебая-Хюккеля:
$mathrm {lggamma_i = — frac {0,5Z_i^{2}sqrt{I}}{1+sqrt{I}}}$ при $mathrm {I leq 0,1 ммоль/л}$
-
Уравнение Дэвиса:
$mathrm {lggamma_i = — frac {0,5Z_i^{2}sqrt{I}}{1+sqrt{I}} + 0,1Z_i^{2}I}$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 14.09.2022



![{displaystyle I={frac {1}{2}}[c(+2)^{2}+c(-2)^{2}]={frac {1}{2}}[4c+4c]=4c}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c3153d34f527dc9229f3cd4402029e72d149cb1)
![{displaystyle {begin{aligned}I&={tfrac {1}{2}}times left[{begin{array}{l}{({text{concentration of }}{ce {Na2SO4}}{text{ in M}})times ({text{number of }}{ce {Na+}})times ({text{charge of }}{ce {Na+}})^{2}} +\{({text{concentration of }}{ce {Na2SO4}}{text{ in M}})times ({text{number of }}{ce {SO4^2-}})times ({text{charge of }}{ce {SO4^2-}})^{2}} +\{({text{concentration of }}{ce {KCl}}{text{ in M}})times ({text{number of }}{ce {K+}})times ({text{charge of }}{ce {K+}})^{2}} +\{({text{concentration of }}{ce {KCl}}{text{ in M}})times ({text{number of }}{ce {Cl-}})times ({text{charge of }}{ce {Cl-}})^{2}}end{array}}right]\&={tfrac {1}{2}}times [{0.050Mtimes 2times (+1)^{2}}+{0.050Mtimes 1times (-2)^{2}}+{0.020Mtimes 1times (+1)^{2}}+{0.020Mtimes 1times (-1)^{2}}]\&=0.17Mend{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a16117298873a1e76082bbf2fbbbaa9f94c27df3)


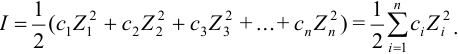
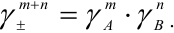
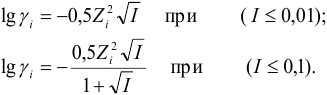
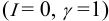 .
.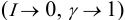 .
.