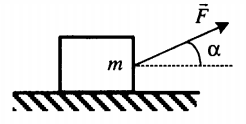
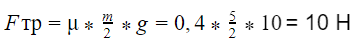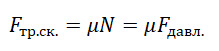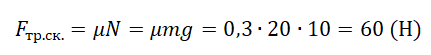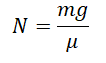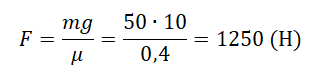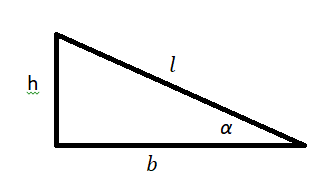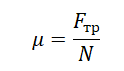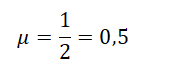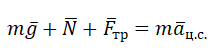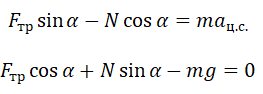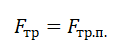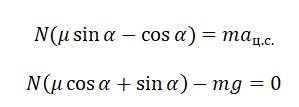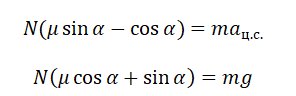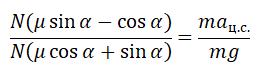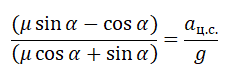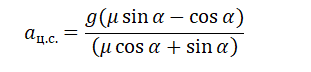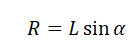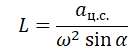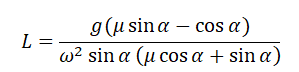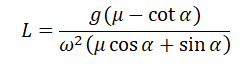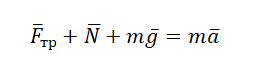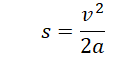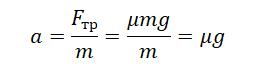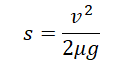{mu = dfrac{F_{тр}}{mg}}
Ускорение свободного падения g
Приводим 2 варианта нахождения коэффициента трения — зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу
mu = dfrac{F_{тр}}{mg}
Fтр — сила трения
m — масса тела
g — ускорение свободного падения (в большинстве задач можно принять g=9.81 м/с²)
Формула коэффициента трения через угол наклона
mu = tg(alpha)
α — угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.
Решение
Для решения задачи воспользуемся формулой.
mu = dfrac{F_{тр}}{mg} = dfrac{50}{20 cdot 9.81} = dfrac{50}{196.2} approx 0.25484
Ответ: approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
mu = tg(alpha) = tg(30°) approx 0.57735
Ответ: approx 0.57735
Проверим полученный ответ с помощью калькулятора .
Эта статья отвечает на вопрос: как найти коэффициент трения? Все мы знаем, что самые гладкие поверхности также имеют некоторые неровности, но мы их не видим.
Если мы их не видим, то как мы будем измерять уровень шероховатости на поверхности? Ответ на этот вопрос кроется в свойстве поверхности, называемом коэффициентом трения. Это дает нам меру того, насколько шероховатая поверхность. В этой статье мы обсудим нахождение коэффициента трения в различных ситуациях.
Что такое трение?
Все мы знаем о трении и его влиянии на нашу жизнь. Противодействующая сила или сопротивление, которое мы чувствуем, толкая что-то вперед, называется трением.
Трение не обязательно плохо. Без трения наша жизнь не была бы такой легкой, если бы не было трения. В этой статье мы узнаем о трении, коэффициенте трения, его использовании и его негативном влиянии на нашу жизнь.
Что такое коэффициент трения?
Коэффициент трения — это свойство поверхности, которое говорит нам о том, насколько она шероховатая.
Мы не можем наблюдать шероховатости невооруженным глазом просто потому, что неровности очень мелкие по своей природе. Нам нужно свойство, которое определяет эти неровности. Это свойство называется коэффициентом трения.
Положительные эффекты трения
Трение часто считают плохим и нежелательным. Это верно во многих областях, но в то же время трение играет очень важную роль и в нашей жизни.
Положительные эффекты трения или преимущества трения приведены в списке ниже:
- тормоза — Тормоза полностью используют трение, чтобы остановить движение автомобиля. Тормоза позволяют шинам сцепляться с неровностями дорожного покрытия. Таким образом, автомобиль перестанет двигаться. Без трения было бы трудно ездить по дорогам, и аварии происходили бы чаще.

Кредиты изображений: анонимные, Дисковый тормоз, CC BY-SA 3.0
- Прогулки — Простая задача, такая как ходьба, также нуждается в помощи трения. Учитывая поверхность с меньшим трением, по которой можно ходить, человек просто соскользнет, если начнёт идти. Это потому, что он не имеет должного сцепления с полом. Подходящей поверхностью для ходьбы является та поверхность, которая не скользкая и имеет лучшее сцепление с дорогой.
- Бег – Бег – это преемник ходьбы. Бег также требует трения, так как трение меньше, а скользкий пол просто приведет к несчастным случаям. Несчастные случаи, которые также могут быть фатальными.
- Зубчатое зацепление – Шестерни имеют зубья, выступающие за пределы колес, которые входят в зацепление с зубьями других шестерен. Зубчатые колеса передают движение одного колеса другому, таким образом, зубчатые колеса выполняют свою функцию с помощью трения.
- Вождение – Вождение автомобиля или велосипеда требует трения, так как трение обеспечивает лучшее сцепление и силу прямой реакции на колеса. Все мы видели, как трудно управлять автомобилем на скользкой дороге, потому что вода смазывает дорогу, делая ее менее скользкой.
- Держа книгу – Держите книгу или, скажем, любой предмет, который нужно держать. Это сцепление обеспечивается трением. Сцепление — это не что иное, как неровности, сцепляющиеся друг с другом.
- Держа карандаш – Подобно тому, как вы держите книгу, держите карандаш – прекрасный пример использования силы трения.
- Катание мяча– Если мяч катится, это не значит, что он будет катиться вечность. Мяч приходит в состояние покоя через некоторое время. Это возможно из-за наличия трения в системе.
Негативные последствия трения
Мы все думаем, что трения нежелательны. Это верно, когда речь идет о местах, где мы требуем от системы максимальной работы. Места, где трение действует как люфт, приведены ниже:
- Выделение тепла при торможении – Выделение тепла в шинах приведет к износу резины, находящейся в шинах. Шины станут плоскими и потребуют обслуживания. Выделение тепла нежелательно в жаркую погоду, так как ущерб будет больше.
- Выделение тепла при работе машин – Выработка тепла в машинах означает, что некоторое количество топлива используется для выработки бесполезного тепла. Следовательно, особое внимание уделяется смазке деталей машин, так как тепло может повредить машины, а также увеличить стоимость эксплуатации.
- Замедление объектов из-за трения – Иногда мы склонны толкать объект на большее расстояние, но трение заставляет его остановиться, прежде чем он достигнет места назначения. Следовательно, нам нужно прикладывать больше усилий при толкании объекта, чтобы он набрал достаточную скорость, чтобы достичь места назначения без каких-либо остановок.
- Трубный поток– Жидкость в трубе замедляется из-за трения между поверхностью трубы и жидкостью. Это приводит к большим потерям в насосах, поскольку им необходимо проталкивать воду с большей силой, чтобы она покрывала потери из-за трения.
Как найти коэффициент трения с массой и силой
Масса объекта отвечает за вес, то есть масса в сочетании с гравитационным притяжением дает вес. Сила трения действует на предмет в силу его шероховатости.
Для расчета коэффициента трения с помощью этих величин используется следующее уравнение:
u= П/С
Где F — сила трения
N — нормальная сила реакции, равная весу тела.
Как рассчитать коэффициент трения с ускорением
Ускорение объекта возникает только при движении объекта. Когда объект движется, в игру вступает кинетическое трение.
Кинетическое трение является постоянной величиной и не может изменяться при любом изменении скорости объекта. Даже если тело движется с ускорением, величина кинетического трения, действующая на тело, будет такой же. Если бы величина кинетического трения также увеличивалась, то ускорение было бы невозможно. Объект не сможет ускориться. Математически кинетическое трение определяется как:
u= F/N= ma/mg= a/g
Здесь сила равна силе, необходимой для того, чтобы объект продолжал двигаться.
Как найти коэффициент трения между двумя материалами
Коэффициент трения можно рассчитать по той же формуле, что и F/N. Чтобы найти коэффициент трения между двумя материалами, мы выполняем следующие шаги:
- Пусть два предмета трутся друг о друга. Этими двумя объектами являются объект A и объект B.
- Когда эти два объекта трутся друг о друга, они приобретают определенную скорость, давайте рассмотрим объект B неподвижным, а объект A движущимся.
- Чтобы заставить объект А двигаться с этой скоростью, требуется сила F.
- Из-за веса объекта на объект B действует сила реакции, обозначаемая как R.
- Чтобы найти коэффициент трения между этими материалами, мы делим силу F на силу реакции R.
Таким образом рассчитывается коэффициент трения между двумя материалами.
Как рассчитать коэффициент трения со скоростью и расстоянием
Мы можем найти значение коэффициента трения, используя скорость и расстояние.
Совершенная работа определяется Fs
Сила, необходимая для совершения работы = F = сила трения = umg
Следовательно, сила, необходимая для остановки объекта = umg.s
Это равно кинетической энергии, то есть KE = O,5 mv^2.
Следовательно, и = (v^2/2g)
Как найти коэффициент трения между двумя поверхностями
Ни одна поверхность не бывает идеально гладкой. В нем будет некоторая шероховатость. Чтобы найти величину шероховатости, нам нужно определить свойство, называемое коэффициентом трения.
Коэффициент трения между двумя поверхностями можно найти, используя тот же метод, который мы обсуждали для нахождения коэффициента трения для двух материалов. Основная формула коэффициента трения остается той же, то есть u = F/N.
Как найти коэффициент трения с энергией
Мы уже обсуждали в предыдущем разделе, что кинетическую энергию можно приравнять к работе, необходимой для остановки движения объекта.
Из вышеприведенного равенства можно найти значение коэффициента трения. Давайте еще раз посмотрим, как мы нашли коэффициент трения с помощью энергии.
Кинетическая энергия- 1/2 мВ^2
Работа, необходимая для того, чтобы объект не двигался — umg.s
Приравнивая обе части, получаем u = v^2/2g
Как найти коэффициент трения с центростремительной силой
Центростремительная сила определяется выражением Fc = mv^2/r
Наблюдения и советы этой статьи мы подготовили на основании опыта команды сила трения действие на объект определяется как – umg
Приравняв обе стороны получим,
и = v ^ 2 / г
Как найти коэффициент трения только по углу
Когда объект движется со наклонная плоскость. Эффект угла вступает в игру. Для наклонной плоскости мы разделяем силы на горизонтальные силы и вертикальные силы.
Коэффициент трения определяется выражением u = F/N
После разрешения получаем u = mgsinA/mgcosA
А — угол, под которым наклонена плоскость.
После решения получаем, u = tanA
Таким образом, мы можем найти коэффициент трения, используя только угол.
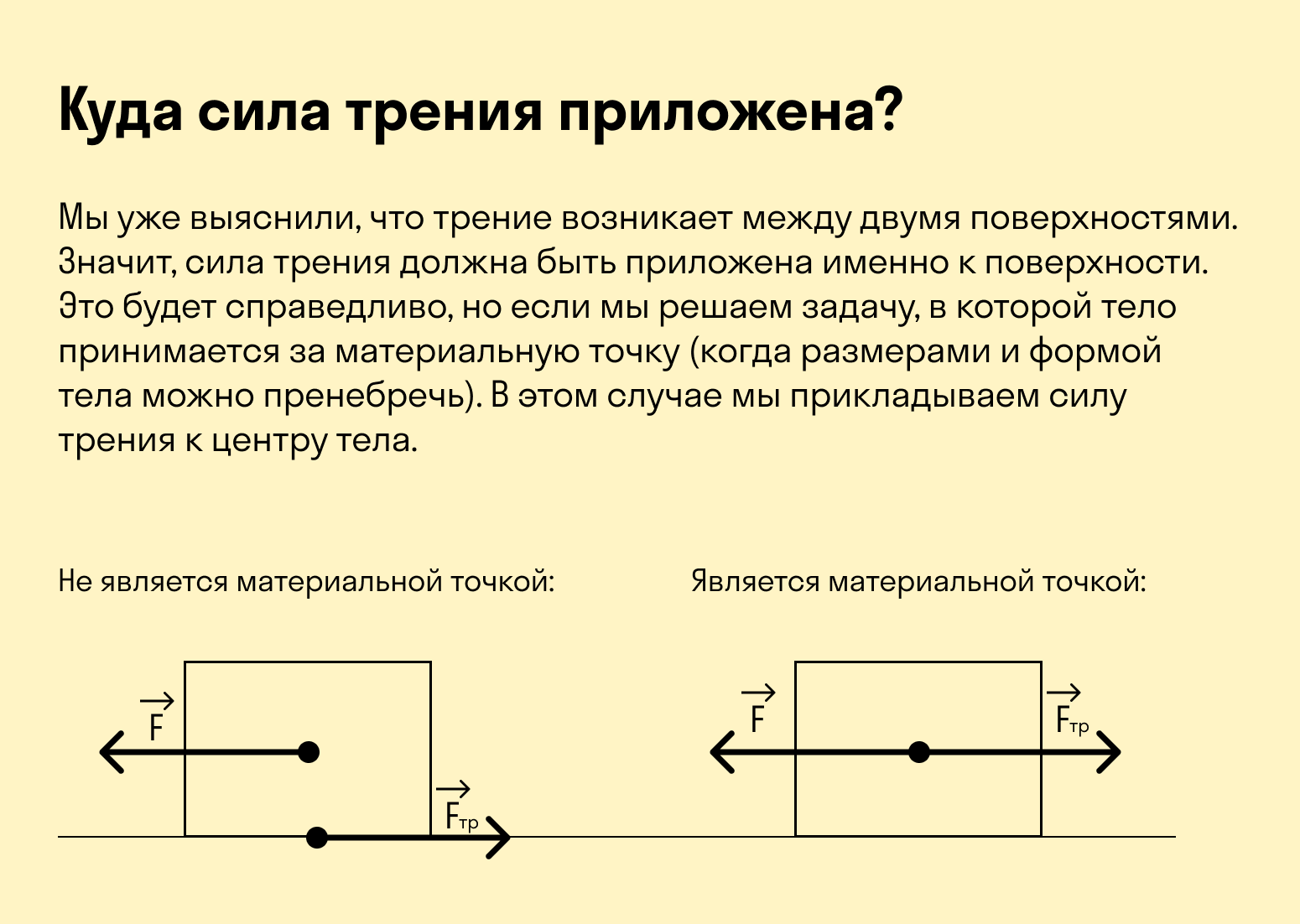
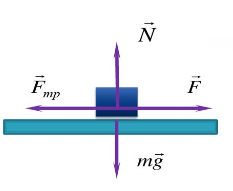
Сила трения: величина, направление
С силой трения вы сталкиваетесь буквально каждую секунду. Каждый раз, когда вы взаимодействуете с любой поверхностью — идете по асфальту, сидите на стуле, пьете чай из чашки — на вас действует сила трения.
Трение — это и есть взаимодействие в плоскости соприкосновения двух поверхностей.
Чтобы перевести трение на язык физики, вводится понятие сила трения.
Сила трения — это величина, которая характеризует процесс трения по величине и направлению.
Измеряется сила трения, как и любая сила — в Ньютонах.
Возникает сила трения по двум причинам:
- Различные шероховатости, царапины и прочие «несовершенства» поверхностей. Эти дефекты задевают друг друга при соприкосновении и создается сила, тормозящая движение.
- Когда контактирующие поверхности практически гладкие (до идеала довести невозможно, но стремиться к нему — значит устремлять силу трения к нулю), то расстояние между ними становится минимальным. В этом случае возникает взаимное притяжение молекул вещества этих поверхностей. Притяжение обусловлено взаимодействием между электрическими зарядами атомов. В связи с этим можно часто услышать формулировку «Сила трения — сила электромагнитной природы»
Направлена сила трения всегда против скорости тела. В этом плане все просто, но всегда есть вопрос:
В задачах часто пишут что-то вроде: «Поверхность считать идеально гладкой». Это значит, что сила трения в данной задаче отсутствует. Да, в реальной жизни это невозможно, но во имя красивой математической модели трением часто пренебрегают.
Не переживайте из-за этой несправедливости, а просто решайте задачи без трения, если увидели словосочетание «гладкая поверхность».
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Пятерка по физике у тебя в кармане!
Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!
Сухое и вязкое трение
Есть очень большая разница между вашим соприкосновением с водой в бассейне во время плавания и соприкосновением между асфальтом и колесами вашего велосипеда.
В случае с плаванием мы имеем дело с вязким трением — явлением сопротивления при движении твердого тела в жидкости или воздухе. Самолет тоже подвергается вязкому трению и вон тот наглый голубь из вашего двора.
А вот сухое трение — это явление сопротивления при соприкосновении двух твердых тел. Например, если школьник ерзает на стуле или злодей из фильма потирает ладоши — это будет сухое трение.
А если злодей чистоплотный и потирает ладоши, капнув на них антисептик?
Тогда это вязкое трение, не смотря на то, что руки — твердые тела. В данном случае есть влажная прослойка.
Вязкое трение в школьном курсе физики не рассматривается подробно, а вот сухое — разбирают вдоль и поперек. У сухого трения также есть разновидности, давайте о них поговорим.
Трение покоя
Если вы решите сдвинуть с места грузовик, вряд ли у вас это получится. Не то, чтобы мы в вас не верим — просто это невозможно сделать из-за того, что масса человека во много раз меньше массы грузовика, да еще и сила трения мешает это сделать. Мир жесток, что тут поделать.
В случае, когда сила трения есть, но тело не двигается с места, мы имеем дело с силой трения покоя.
Сила трения покоя равна силе тяги. Например, если вы пытаетесь сдвинуть с места санки, действуя на них с силой тяги 10 Н, то сила трения будет равна 10 Н.
Сила трения покоя
Fтр = Fтяги
Fтр — сила трения покоя [Н]
Fтяги — сила тяги [Н]
Немного потренируемся!
Задача
Найти силу трения покоя для тела, на которое действуют сила тяги в 4 Н.
Решение:
Тело покоится, значит
Fтр = Fтяги = 4 Н
Ответ: сила трения равна 4 Н.
Трение скольжения
А теперь давайте скользить на коньках по льду. Каток достаточно гладкий, но, как мы уже выяснили, сила трения все равно будет присутствовать и вычисляться будет по формуле:
Сила трения скольжения
Fтр = μN
Fтр — сила трения скольжения [Н]
μ — коэффициент трения [—]
N — сила реакции опоры [Н]
Сила трения, которую мы получим по этой формуле будет максимально возможной — то есть больше уже некуда.
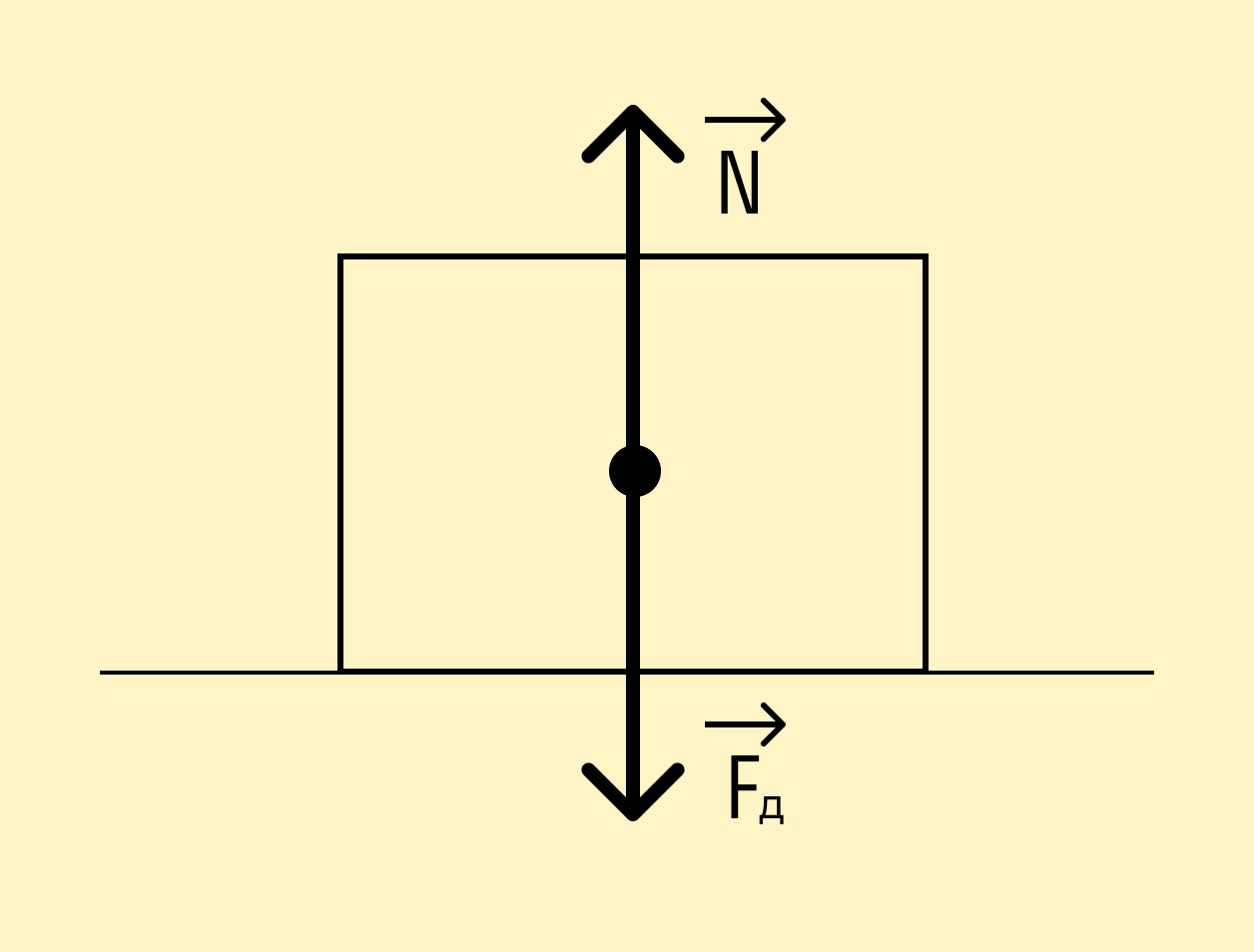
Сила реакции опоры — это сила, с которой опора действует на тело. Она численно равна силе нормального давления и противоположна по направлению.
Сила нормального давления — это то же самое, что и вес тела?
Не совсем. Сила нормального давления направлена всегда перпендикулярно поверхности (нормаль — перпендикуляр к поверхности). Вес не обязательно направлен перпендикулярно поверхности.
В рамках школьного курса вес всегда направлен перпендикулярно поверхности, поэтому силу реакции опоры можно численно приравнивать к весу.
Подробнее про вес тела читайте в нашей статье😇
Также, если тело находится на горизонтальной поверхности, сила реакции опоры будет равна силе тяжести: N = mg.
Коэффициент трения — это характеристика поверхности. Он определяется экспериментально, не имеет размерности и показывает, насколько поверхность гладкая — чем больше коэффициент, тем более шероховатая поверхность. Коэффициент трения положителен и чаще всего меньше единицы.
Будем бдительны!
Из формулы не следует зависимость силы трения от площади соприкосновения. Например, если вы положите брусок на один бок и протащите по столу, а потом перевернете на другой, не равный по площади, и сделаете то же самое — сила трения не изменится.
Задача 1
Масса котика, лежащего на столе, составляет 5 кг. Коэффициент трения µ = 0,2. К коту прилагают внешнюю силу, равную 2,5 Н. Какая сила трения при этом возникает?
Решение:
По условию данной задачи невозможно понять, двигается наш котик или нет. Решение о том, приравниваем ли мы к силе тяги силу трения, принять сразу нельзя. В таких случаях нужно все-таки рассчитать по формуле:
F = μN
Так как котик лежит на горизонтальной поверхности, сила реакции опоры в данном случае равна силе тяжести: N = mg.
F = μmg = 0,2 · 5 · 10 = 10Н
Мы получили максимально возможную силу трения. Внешняя сила по условию задачи меньше максимальной. Это значит, что котик находится в покое. Сила трения уравновешивает внешнюю силу. Следовательно, она равняется 2,5 Н.
Ответ: возникает сила трения величиной 2,5 Н
Задача 2
Барсук скользит по горизонтальной плоскости. Найти коэффициент трения, если сила трения равна 5 Н, а сила давления тела на плоскость — 20 Н.
Решение:
В данной задаче нам известно, что барсучок скользит. Значит нужно воспользоваться формулой:
Fтр = μN
Так как барсук находится на горизонтальной поверхности, сила реакции опоры в данном случае равна силе давления на плоскость: N = Fд.
Fтр = μFд
Выражаем коэффициент трения:
μ = Fтр / Fд = 5 / 20 = 0,25
Ответ: коэффициент трения равен 0,25
Задача 3
Пудель вашей бабушки массой 5 кг скользит по горизонтальной поверхности. Сила трения скольжения равна 20 Н. Найдите силу трения, если пудель сильно похудеет, и его масса уменьшится в два раза, а коэффициент трения останется неизменным.
Решение:
В данной задаче нам известно, что пудель скользит. Значит, нужно воспользоваться формулой:
Fтр = μN
Так как пудель находится на горизонтальной поверхности, сила реакции опоры в данном случае равна силе тяжести: N = mg.
Fтр = μmg
Выразим коэффициент трения:
μ = Fтр / mg = 20 / 5 · 10 = 0,4
Теперь рассчитаем силу трения для массы, меньшей в два раза:
Ответ: сила трения будет равна 10 Н.
Задача 4
Ученик провел эксперимент по изучению силы трения скольжения, перемещая брусок с грузами равномерно по горизонтальным поверхностям с помощью динамометра.
Результаты экспериментальных измерений массы бруска с грузами m, площади соприкосновения бруска и поверхности S и приложенной силы F представлены в таблице.
Какие утверждения соответствуют результатам проведенных экспериментальных измерений? Из предложенного перечня утверждений выберите два правильных.
-
Коэффициенты трения скольжения во втором и третьем опытах равны.
-
Коэффициент трения скольжения между бруском и деревянной рейкой больше коэффициента трения скольжения между бруском и пластиковой рейкой.
-
Сила трения скольжения зависит от площади соприкосновения бруска и поверхности.
-
Сила трения скольжения зависит от рода соприкасающейся поверхности.
Решение:
Подробно рассмотрим каждое утверждение.
-
В данном случае сила реакции опоры равна силе тяжести. Значит Fтр = μN = μmg.
Выразим коэффициент трения скольжения:
μ = Fтр / mgКоэффициент трения скольжения во втором опыте равен 0,4 / (0,2 · 10) = 0,2.
В третьем опыте — 0,4 / (0,1 · 10) = 0,4.
Следовательно, утверждение «Коэффициенты трения скольжения во втором и третьем опытах равны» неверно.
-
Как и в первом утверждении, коэффициент трения будет вычисляться по формуле:
μ = Fтр / mgДля деревянной рейки μ = Fтр / mg = 0,8 / 0,2 · 10 = 0,4
Для пластиковой рейки μ = Fтр / mg = 4,8 / 0,2 · 10 = 0,2
Следовательно утверждение «Коэффициент трения скольжения между бруском и деревянной рейкой больше коэффициента трения скольжения между бруском и пластиковой рейкой» верно.
-
Согласно формуле Fтр = μN, сила трения не зависит от площади поверхности соприкосновения. Значит утверждение «Сила трения скольжения зависит от площади соприкосновения бруска и поверхности» неверно.
-
Если проанализировать первый и второй эксперимент, можно увидеть, что при прочих равных данных сила меняется. Это значит, что утверждение «Сила трения скольжения зависит от рода соприкасающейся поверхности» верно.
Ответ: 25
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Трение качения
Про колесо совершенно точно нельзя сказать, что оно скользит или покоится. При этом сила трения явно возникает, так как существует соприкосновение двух поверхностей.
В этом случае мы говорим о трении качения — сопротивлению движения, если одно тело катится по поверхности другого. При равных силах нормального давления сила трения скольжения больше силы трения качения. Это явление часто используют, например, ставя колесики на чемодан. Да и вообще, ставя колесики куда угодно.
Сила трения качения
Fтр = (λN)/R
Fтр — сила трения качения [Н]
λ — коэффициент трения качения [м]
N — сила реакции опоры [Н]
R — радиус колеса [м]
Задачи на трение качения встречаются только в задачах высокого уровня сложности (например, в олимпиадах). Однако на формулу посмотреть полезно, даже если вы не планируете покорять самую высокую вершину.
Если приглядеться, она очень похожа на формулу трения скольжения, только в знаменателе появляется радиус. Если мы будем увеличивать знаменатель, то сила трения будет уменьшаться. То есть, чем больше радиус колеса, тем меньше трение.
Ладно, давайте все-таки решим задачу на силу трения качения — только никому об этом не рассказывайте 😉
Задача
Какого радиуса понадобится установить колесо, чтобы уменьшить силу трения, равную 17 Н — на 5 Н. При коэффициенте трения 0,6 мм и силе нормального давления тела равной 10 кН.
Решение:
Берем формулу силы трения качения:
Fтр = (λN)/R
Выражаем из нее радиус:
R = (λN)/Fтр
Коэффициент трения качения и сила нормального давления нам даны, а чтобы найти силу трения, нам нужно вычесть из начальной силы трения ее изменение:
Fтр 2 = Fтр 1 − ΔFтр = 17 − 5 = 12Н
Подставляем числа в формулу, предварительно переведя их в СИ:
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
R = (λN)/Fтр = 0,0006 · 10 000 / 12 = 0,5 м
Ответ: необходимо поставить колесо радиусом 0,5 м.
Избавиться от трения: возможно ли это
Итак, идеально гладких поверхностей в реальной жизни не бывает. Это значит, что стараясь делать поверхность идеально гладкой — например, натирая ее миллион часов супер-мелкой наждачной бумагой — мы минимизируем трение, но не избавляемся от него.
Но это не значит, что способов избавиться от трения не существует. Например, вполне себе реальны поезда на магнитных подушках. Благодаря магнитному полю, которое создается между рельсом и вагоном, поезд как будто бы парит. Так он ликвидирует соприкосновение различных поверхностей, из-за которого и создается трение.
Трение — вариант взаимодействия двух тел. Оно возникает при движении одного тела по поверхности другого. При этом тела действуют друг на друга с силой, которая называется силой трения. Сила трения имеет электромагнитную природу.
Сила трения — сила, возникающая между телами при их движении или при попытке их сдвинуть. Обозначается как Fтр. Единица измерения — Н (Ньютон).
Трение бывает сухим и жидким. В школьном курсе физике изучается сухое трение.
Виды сухого трения:
- трение скольжения;
- трение качения;
- трение покоя.
Трение скольжения
Трение скольжения — трение, возникающее при скольжении одного тела по поверхности другого. Сила трения скольжения направлена противоположно направлению движения тела: Fтр↑↓v.
Сила трения скольжения определяется формулой:
μ — коэффициент трения, N — сила реакции опоры, Fдавл. — сила нормального давления
Сила реакции опоры и сила нормального давления — равные по модулю, но противоположные по направлению силы. Если тело не перемещается с ускорением относительно оси ОУ, модули силы реакции опоры и силы нормального давления равны модулю силы тяжести, действующей на это тело.
Силу трения скольжения зависит от степени неровности (шероховатости) поверхности. Поэтому ее можно легко менять.
Чтобы увеличить силу трения скольжения, нужно сделать поверхность тела более шероховатой. Так, чтобы зимой автомобили не скользили по голому льду, автомобилисты используют зимние шины. От летних они отличаются глубоким протектором и наличием шипов, создающих дополнительную неровность.
Чтобы уменьшить силу трения скольжения, нужно сделать поверхность более ровной. Ее можно отшлифовать или смазать. Так, чтобы лыжи скользили по снегу лучше, их смазывают специальными мазями или парафинами.
Полезные факты
- Если тело движется по гладкой поверхности, сила трения между ними отсутствует.
- Сила трения скольжения не зависит от площади соприкосновения тел.
- Сила трения качения обычно в несколько раз меньше силы трения скольжения. Поэтому тяжелые грузы перемещают не волоком, а с помощью тележек на колесах.
Пример №1. Конькобежец массой 70 кг скользит по льду. Какова сила трения, действующая на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,002?
Сила реакции опоры по модулю равна силе тяжести, действующей на конькобежца. Отсюда:
Трение покоя
Трение покоя возникает при попытке сдвинуть предмет с места. Трение покоя противоположно направлено приложенной к телу силе (в сторону возможного движения).
Сила трения покоя всегда больше нуля, но всегда меньше силы трения скольжения:
0 < Fтр.пок. < Fтр. ск.
Способы определения вида силы трения, возникающей между телами, и ее модуля:
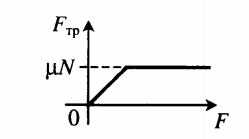
- Когда к телу прикладывается сила F , модуль которой меньше силы трения скольжения, возникает сила трения покоя. Тело продолжает покоиться. При этом модуль силы трения покоя равен модулю прикладываемой к телу силы. Если F < Fтр. ск., Fтр.пок. = F.
- Когда к телу прикладывается сила, модуль которой равен силе трения скольжения или превышает ее, возникает сила трения скольжения. Тело при этом начинает двигаться. Сила трения определяется формулой силы трения скольжения. Если F ≥ Fтр. ск., Fтр. = Fтр.ск.
Графически это можно изобразить так:
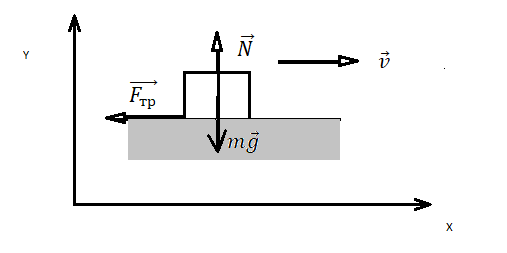
Пример №2. На горизонтальном полу стоит ящик массой 20 кг. Коэффициент трения между полом и ящиком равен 0,3. К ящику в горизонтальном направлении прикладывают силу 36 Н. Какова сила трения между ящиком и полом?
Чтобы определить вид трения, возникающего между ящиком и полом, нужно найти силу трения скольжения и сравнить с ней приложенную к ящику силу.
Сила, приложенная к ящику, меньше силы трения скольжения. Значит, между ящиком и полом возникает сила трения покоя. Модуль силы трения покоя равен модулю приложенной силы:
Fтр.пок. = F = 36 (Н).
Описание движения тел с учетом сил трения
Тело может двигаться по горизонтальной, наклонной или вертикальной плоскости. Оно может покоиться, двигаться равномерно или с ускорением, а сила тяги, под действием которой движется тело, может быть направлена, как в сторону движения тела, так и под углом к плоскости. Поэтому применение законов Ньютона к каждому из случаев имеет свои особенности.
Движение тела по горизонтальной плоскости
Равноускоренное движение по горизонтали, сила тяги параллельная плоскости |
|
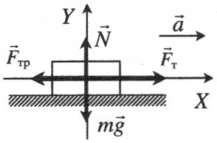 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fт – Fтр = ma Проекция на ось ОУ: N – mg = 0 |
Равнозамедленное движение по горизонтали, сила тяги параллельная плоскости |
|
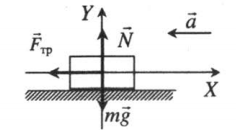 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: – Fтр = –ma Проекция на ось ОУ: N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вверх) |
|
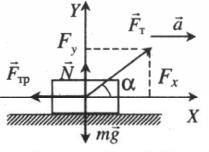 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: Fтsinα + N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вниз) |
|
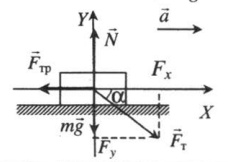 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: N – Fтsinα – mg = 0 |
Внимание! В случаях, когда сила тяги Fт направлена под углом к плоскости движения, сила реакции опоры не равна силе тяжести: N ≠ mg.
Пример №3. Брусок массой 1 кг движется равноускоренно по горизонтальной поверхности под действием силы 10 Н, как показано на рисунке. Коэффициент трения скольжения равен 0,4, а угол наклона α — 30 градусов. Чему равен модуль силы трения?
Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры:
Fтр = μN
Проекция сил на ось ОУ выглядит так:
N – Fтsinα – mg = 0
Отсюда силы реакции опоры равна:
N = Fтsinα + mg
Подставим ее в формулу для вычисления силы трения и получим:
Fтр = μN = μ (Fтsinα + mg) = 0,4(10∙0,5 + 1∙10) = 6 (Н)
Движение тела по вертикальной плоскости
Тело прижали к вертикальной плоскости и удерживают |
|
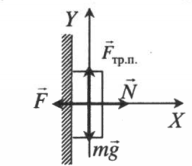 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – F = 0 Проекция на ось ОУ: Fт.п. – mg = 0 |
Тело поднимается под действием силы тяги, направленной под углом к вертикали |
|
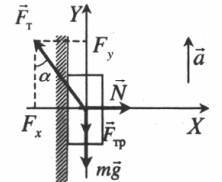 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – Fтsinα = 0 Проекция на ось ОУ: Fтcosα – Fтр – mg = 0 |
Пример №4. Груз массой 50 кг удерживают на вертикальной плоскости, коэффициент трения которой равен 0,4. Определить, какую силу нужно приложить, чтобы груз оставался в состоянии покоя.
Проекция на ось ОХ:
N – F = 0
Отсюда следует, что сила должна быть равна силе реакции опоры.
Проекция на ось ОУ:
Fт.п. – mg = 0
Перепишем, выразив силу трения через силу реакции опоры:
μN – mg = 0
Отсюда выразим силу реакции опоры:
Следовательно:
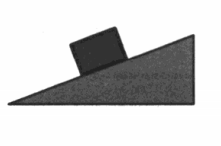
Движение тела по наклонной плоскости
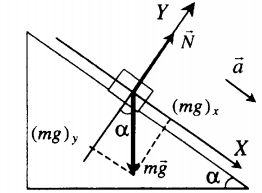
Движение вниз без трения |
|
 |
Второй закон Ньютона в векторной форме: |
|
mg + N = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело покоится на наклонной плоскости |
|
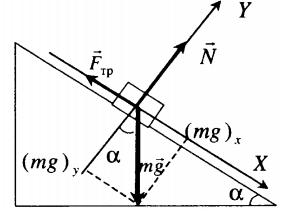 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα – Fтр.п. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело удерживают на наклонной плоскости |
|
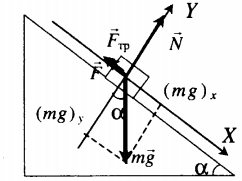 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
F + Fтр. – mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равноускоренное движение вверх с учетом силы трения |
|
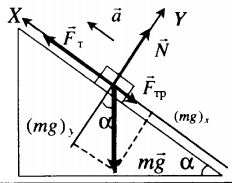 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fт + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равномерное движение вверх с учетом силы трения |
|
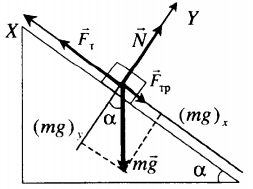 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
Пример №5. Брусок массой 200 г покоится на наклонной плоскости. Коэффициент трения между поверхностью бруска и плоскостью равен 0,6. Определите величину силы трения, если угол наклона плоскости к горизонту равен 30 градусам.
Переведем массу в килограммы: 200 г = 0,2 кг.
Проекция сил, действующих на тело, на ось ОХ:
mg sinα – Fтр.п. = 0
Отсюда сила трения равна:
Fтр.п. = mg sin α
Подставляем известные данные и вычисляем:
Fтр.п. = 0,2∙10∙sin30o = 2∙0,5 = 1 (Н)
Полезная информация
Задание EF18204
При исследовании зависимости силы трения скольжения Fтр от силы нормального давления Fд были получены следующие данные:
|
Fтр, Н |
1,0 |
2,0 |
3,0 |
4,0 |
|
Fд, Н |
2,0 |
4,0 |
6,0 |
8,0 |
Из результатов исследования можно сделать вывод, что коэффициент трения скольжения равен:
а) 0,2
б) 2
в) 0,5
г) 5
Алгоритм решения
1.Записать формулу, связывающую силу трения с силой нормального давления.
2.Выразить из нее коэффициент трения.
3.Взять значения силы трения и силы нормального давления из любого опыта (из любого столбца таблицы).
4.Вычислить коэффициент трения на основании табличных данных.
Решение
Силу трения и силу нормального давления связывает формула:
Fтр = μN
Отсюда коэффициент трения равен:
Сделаем расчет коэффициента трения на основании данных первого опыта (1 столбца):
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17513
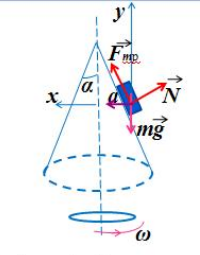
Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу.
Алгоритм решения
1.Построить чертеж. Указать все силы, действующие на шайбу. Выбрать систему координат.
2.Записать второй закон Ньютона для описания движения шайбы в векторном виде.
3.Записать второй закон Ньютона в виде проекций на оси.
4.Через систему уравнений вывести искомую величину.
Решение
Так как шайба вращается, покоясь на поверхности конуса, на нее действуют четыре силы: сила трения, сила тяжести, сила реакции опоры и центростремительная сила. Изобразим их на чертеже. Выберем систему координат, параллельную оси вращения.
Второй закон Ньютона в векторном виде выглядит следующим образом:
Теперь запишем этот закон в проекциях на оси ОХ и ОУ соответственно:
Так как шайба покоится относительно поверхности конуса, сила трения равна силе трения покоя:
Максимальное значение силы трения равно:
Принимая в учет силу трения покоя, проекции на оси ОХ и ОУ примут следующий вид:
Запишем систему уравнение в следующем виде:
Поделим первое уравнение на второе и получим:
Сделаем сокращения и получим:
Отсюда центростремительное ускорение равно:
Но также известно, что центростремительное ускорение равно произведению квадрата угловой скорости на радиус окружности:
Радиус окружности, по которой вращается шайба вместе с конусом, можно вычислить по формуле:
Отсюда центростремительное ускорение равно:
Выразим искомую величину L:
Подставим в это выражение выведенную для центростремительного ускорения формулу и получим:
Поделим числитель на синус угла α, чтобы упростить выражение, и получим:
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18051
Грузовик массой m, движущийся по прямолинейному горизонтальному участку дороги со скоростью υ, совершает торможение до полной остановки. При торможении колёса грузовика не вращаются. Коэффициент трения между колёсами и дорогой равен μ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать исходные данные.
2.Сделать чертеж. Указать все силы, действующие на грузовик во время торможения. Выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме.
4.Записать второй закон Ньютона в виде проекций на оси ОХ и ОУ.
5.Записать формулу для нахождения силы трения скольжения.
6.Записать формулу для расчета перемещения при движении с постоянным ускорением.
7.Использовать второй закон Ньютона для определения тормозного пути.
Решение
Из условий задачи нам известны следующие величины:
• Начальная скорость грузовика (до начала торможения) v0 = v.
• Коэффициент трения между колесами и дорогой μ.
Выполним чертеж. Выберем такую систему координат, в которой направление движения грузовика во время торможения совпадает с направлением оси ОХ:
Запишем второй закон Ньютона в векторной форме:
Запишем второй закон Ньютона в проекциях на оси:
Fтр = ma
N – mg = 0
Известно, что сила трения скольжения определяется формулой:
Fтр = μN = μmg
Значит, в первую ячейку таблицы мы должны поставить «1».
Перемещение при равнозамедленном движении определяется формулой (учтем, что конечная скорость равна 0, так как грузовик остановился):
Выразим ускорение через проекцию сил на ось ОХ:
Подставим найденное ускорение в формулу тормозного пути и получим:
Следовательно, во вторую ячейку таблицы мы должны поставить «4».
Полный ответ: «14».
Ответ: 14
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 14.5k
Коэффициент трения
Определение и формула коэффициента трения
Коэффициент трения — это основная характеристика трения как явления. Он определяется видом и состоянием поверхностей трущихся тел.
Данный коэффициент трения не зависит от площадей, соприкасающихся поверхностей.
В данном случае речь идет о коэффициенте трения скольжения, который зависит от совокупных свойств трущихся поверхностей и является безразмерной величиной. Коэффициент трения зависит от: качества обработки поверхностей, трущихся тел, присутствия на них грязи, скорости движения тел друг относительно друга и т.д. Коэффициент трения определяют эмпирически (опытным путем).
Коэффициент трения, который соответствует максимальной силе трения покоя в большинстве случаев больше, чем коэффициент трения движения.
Для большего числа пар материалов величина коэффициента трения не больше единицы и лежит в пределах
Угол трения
Иногда вместо коэффициента трения применяют угол трения (), который связан с коэффициентом соотношением:
Так, угол трения соответствует минимальному углу наклона плоскости по отношению к горизонту, при котором тело, лежащее на этой плоскости, начнет скользить вниз под воздействием силы тяжести. При этом выполняется равенство:
Истинный коэффициент трения
Закон трения, который учитывает влияние сил притяжения между молекулами, трущихся поверхностей записываю следующим образом:
где — называют истинным коэффициентом трения,
— добавочное давление, которое вызывается силами межмолекулярного притяжения, S — общая площадь непосредственного контакта трущихся тел.
Коэффициент трения качения
Коэффициент трения качения (k) можно определить как отношение момента силы трения качения () к силе с которой тело прижимается к опоре (N):
Отметим, что коэффициент трения качения обозначают чаще буквой . Этот коэффициент, в отличие от выше перечисленных коэффициентов трения, имеет размерность длины. То есть в системе СИ он измеряется в метрах.
Коэффициент трения качения много меньше, чем коэффициент трения скольжения.