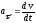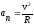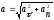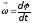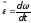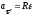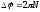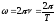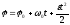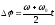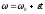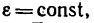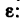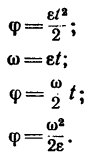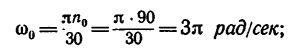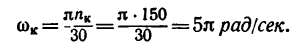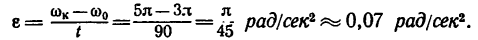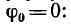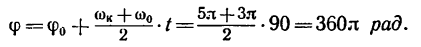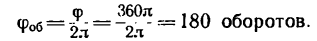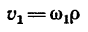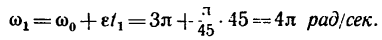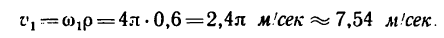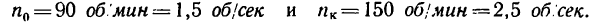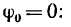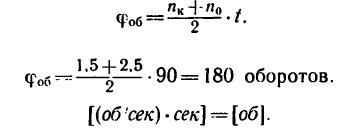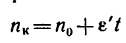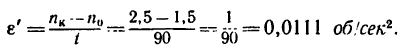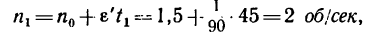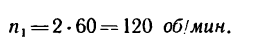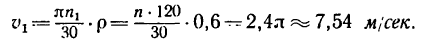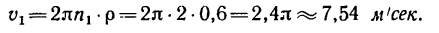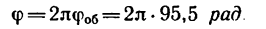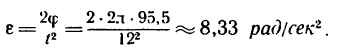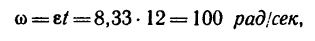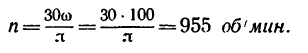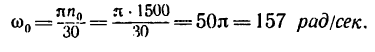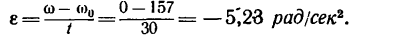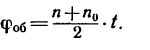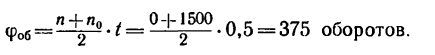Как найти количество оборотов до остановки - AutoPluse.ru

сколько оборотов совершит тело до остановки

04.12.2013, 17:13. Показов 10257. Ответов 2

Доброго времени суток, форумчане!
Помогите пожалуйста получить формулу

Тело вращается по оси.
Даны:
начальная угловая скорость
момент инерции
момент силы (момент торможения)
ну и др. величины, понимаю, что вопрос может быть не точным, потому если каких-то параметров не хватает — укажите пожалуйста.
нужно найти кол-во оборотов N, до остановки вращения.

время, до остановки, если я всё правильно посчитал(об/сек -> : ),
но тут это не пригодится, как я понимаю
Спасибо.

Источник

– величина
тангенциального (касательного) ускорения;

– величина
нормального (центростремительного)
ускорения;

– полное
ускорение;

– модуль
полного ускорения;

– угловая
скорость;

– угловое
ускорение;

;
;

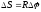
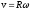
– связь линейных и угловых величин
(путь, скорость и ускорение);

– угловой
путь;

– связь
угловой скорости с частотой и периодом
вращения.

Равнопеременное
вращательное движение (ε=const):

– угловая
координата;

;

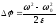
– угловой путь;

– угловая
скорость.

Колесо,
вращаясь равнозамедленно, при торможении
уменьшило свою частоту за 1 минуту от
300 об/мин до 180 об/мин. Найти угловое
ускорение колеса и число оборотов,
сделанных им за это время. Через какое
время колесо остановится?
Вал
вращается со скоростью, соответствующей
частоте 180 об/мин. С некоторого момента
вал тормозится и вращается равнозамедленно
с угловым ускорением, численно равным
3 рад/с².
Через сколько времени вал остановится?
Сколько оборотов он сделает до остановки?
Точка
движется по окружности радиусом 20 см
с постоянным тангенциальным ускорением
5 см/с².
Через сколько времени после начала
движения нормальное ускорение точки
будет равно тангенциальному?
Найти
угловое ускорение колеса, если известно,
что через 2 с после начала равноускоренного
движения вектор полного ускорения
точки, лежащей на ободе, составляет
угол 60⁰
с направлением линейной скорости этой
точки.
Колесо
радиусом 0.1 м вращается так, что
зависимость угла поворота радиуса
колеса от времени дается уравнением
j=A+Bt²+Ct³,
где B=2
рад/с, С=1 рад/с².
Для точек, лежащих на ободе колеса,
найти через 2 с после начала движения:
угловую скорость; линейную скорость;
угловое ускорение; тангенциальное
ускорение; нормальное ускорение; полное
ускорение.
Колесо
радиусом 5 см вращается так, что
зависимость угла поворота радиуса
колеса от времени дается уравнением
j=A+Bt+Ct²+Dt³,
где D=1
рад/с³.
Найти для точек, лежащих на ободе колеса,
изменение тангенциального ускорения
за каждую секунду движения.
Колесо
радиусом 30 см вращается так, что
зависимость линейной скорости точек,
лежащих на ободе колеса, от времени
движения дается уравнением: v=3t+t²
(скорость – в м/с, время – в секундах).
Найти угол, составляемый вектором
полного ускорения с радиусом колеса в
момент времени 5 с после начала движения.
Поезд
въезжает на закругленный участок пути
с начальной скоростью 54 км/ч и проходит
равноускоренно путь 600 м за время 30 с.
Радиус закругления 1 км. Найти скорость
и полное ускорение поезда в конце этого
участка пути.
Камень
брошен горизонтально со скоростью 10
м/с. Найти нормальное и тангенциальное
ускорение камня и радиус кривизны
траектории через 3 с после начала
движения.
Воздушный
шар начинает подниматься с поверхности
Земли. Скорость его подъема постоянна
и равна υ_о.
Благодаря ветру шар приобретает
горизонтальную компоненту скорости
υ_х=Aу,
где A
—
постоянная, у
—
высота подъема. Найти зависимости от
высоты подъема: а) величины сноса шара
х(у);
б) полного, тангенциального и нормального
ускорений шара.
Автомобиль
движется по закруглению шоссе, имеющему
радиус кривизны 50 м. Длина пути автомобиля
выражается уравнением S=10+10t+0.5t²
(путь – в метрах, время – в секундах).
Найти скорость автомобиля, его
тангенциальное, нормальное и полное
ускорения через 5 с после начала движения.
Материальная
точка движется по окружности радиуса
80 см по закону S=10t–0.1t³
(путь в метрах, время в секундах). Найти
скорость, тангенциальное, нормальное
и полное ускорения через 2 с после начала
движения.
По
дуге окружности радиуса 10 м движется
точка. В некоторый момент времени
нормальное ускорение точки равно 5
м/с²,
а вектор полного ускорения образует в
этот момент с вектором нормального
ускорения угол 60⁰.
Найти скорость и тангенциальное
ускорение точки.
Зависимость
пройденного телом пути от времени
дается уравнением S=A+Bt+Ct²+Dt³,
где С=0.14 м/с²,
D=0.01
м/с³.
Через сколько времени после начала
движения ускорение тела будет равно 1
м/с²?
Чему равно среднее ускорение тела за
этот промежуток времени?
Тело
брошено со скоростью 14.7 м/с под углом
30⁰
к горизонту. Найти нормальное и
тангенциальное ускорение тела через
1.25 с после начала движения.
Тело
брошено горизонтально со скоростью 15
м/с. Найти нормальное и касательное
ускорение через 1 с после начала движения.
Тело
брошено со скоростью 10 м/с под углом
45⁰
к горизонту. Найти радиус кривизны
траектории тела через 1 с после начала
движения.
Тело
брошено со скоростью v₀
под углом a
к горизонту. Найти величины v₀
и a,
если наибольшая высота подъема тела 3
м и радиус кривизны траектории тела в
верхней точке траектории 3 м.
Колесо,
вращаясь равноускоренно, достигло
угловой скорости 20 рад/с через 10 оборотов
после начала вращения. Найти угловое
ускорение колеса.
Маховое
колесо спустя 1 минуту после начала
вращения приобретает скорость,
соответствующую частоте 720 об/мин. Найти
угловое ускорение колеса и число
оборотов колеса за эту минуту. Вращение
считать равноускоренным.
Вентилятор
вращается со скоростью, соответствующей
частоте 900 об/мин. После выключения
вентилятор, вращаясь равнозамедленно,
сделал до остановки 75 оборотов. Сколько
времени прошло с момента выключения
вентилятора до его остановки?
Точка
движется по окружности радиусом 10 см
с постоянным тангенциальным ускорением.
Найти тангенциальное ускорение точки,
если к концу пятого оборота после начала
движения скорость точки стала 79.2 см/с.
Точка
движется по окружности с постоянным
тангенциальным ускорением. Найти
нормальное ускорение точки через 20 с
после начала движения, если к концу
пятого оборота после начала движения
линейная скорость точки равна 10 см/с.
Колесо
радиусом 10 см вращается с постоянным
угловым ускорением 3.14 рад/с².
Найти для точек на ободе колеса к концу
первой секунды после начала движения
угловую скорость; линейную скорость;
тангенциальное ускорение; нормальное
ускорение; полное ускорение.
Точка
движется по окружности радиусом 2 см.
Зависимость пути от времени дается
уравнением S=0.1t³
(путь – в метрах, время – в секундах).
Найти нормальное и тангенциальное
ускорения точки в момент, когда линейная
скорость точки равна 0.3 м/с.
Точка
движется по окружности так, что
зависимость пути от времени дается
уравнением S=A+Bt+Ct²,
где B=–2
м/с и С=1 м/с².
Найти линейную скорость точки, ее
тангенциальное, нормальное и полное
ускорения через 3 с после начала движения,
если нормальное ускорение точки в
момент времени 2 с равно 0.5 м/с².
Колесо
вращается с постоянным угловым ускорением
2 рад/с².
Через 0.5 с после начала движения полное
ускорение колеса стало равно 13.6 см/с².
Найти радиус колеса.
Колесо
вращается так, что зависимость угла
поворота радиуса колеса от времени
дается уравнением j=A+Bt+Ct²+Dt³,
где B=1
рад/с, С=1 рад/с²,
D=1
рад/с³.
Найти радиус колеса, если известно, что
к концу второй секунды движения
нормальное ускорение точек, лежащих
на ободе колеса, равно 3.46 м/с².
Маховое
колесо, вращающееся с частотой 240 об/мин,
останавливается в течение 30 с. Найти
число оборотов, сделанных колесом до
полной остановки.
На
цилиндр, который может вращаться около
горизонтальной оси, намотана нить, к
концу которой привязан грузик. Двигаясь
равноускоренно, грузик за 3 с опустился
на 1.5 м. Определить угловое ускорение
цилиндра, если его радиус равен 4 см.
Тело
вращалось равноускоренно с начальной
частотой 40 об/мин. После того, как
совершилось 20 оборотов телом, частота
увеличилась до 120 об/мин. Найти угловое
ускорение и время, в течение которого
изменялась частота.
Шкив
радиусом 20 см приводится во вращение
грузом, подвешенным на нити, постепенно
сматывающейся со шкива. В начальный
момент груз был неподвижен, а затем
стал опускаться с ускорением 20 см/с².
Определить угловую скорость шкива в
тот момент, когда груз пройдет путь 1
м.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Равнопеременное вращательное движение:

Вращательное движение с переменной угловой скоростью называется неравномерным. Если же угловое ускорение

и уравнение, выражающее угловую скорость тела в любой момент времени,

представляют совокупность основных формул вращательного равнопеременного движения тела.

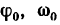
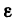
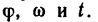
В эти формулы входят всего шесть величин: три постоянных для данной задачи и и три переменных Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин.

Для удобства решения некоторых задач из уравнений (1) и (2) можно получить еще две вспомогательные формулы.

Исключим из (1) и (2) угловое ускорение

Исключим из (1) и (2) время t:

В частном случае равноускоренного вращения, начавшегося из состояния покоя, 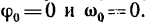Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид:

Задача №1

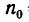
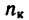
Маховик, вращающийся с угловой скоростью = 90 об/мин, с некоторого момента начинает вращаться равноускоренно и через 1,5 мин достигает угловой скорости = — 150 об/мин. Определить угловое ускорение маховика. Сколько всего оборотов делает маховик за 1,5 мин? Какую скорость имеют точки на цилиндрической поверхности маховика через 45 сек после начала равноускоренного движения, если диаметр маховика 1,2 м?

Решение 1. Все угловые величины выражаем в радианном измерении.

1. Если 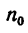=90 об/мин, то

если 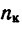=150 об/мин, то

2. Из уравнения (2) находим угловое ускорение, учитывая, что изменение угловой скорости от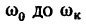 происходит за t=1,5 мин = 90 сек:

3. Определяем из формулы (3) угол поворота тела за t = 1,5 мин = 90 сек, принимая

4. Находим, какому числу оборотов соответствует этот угол поворота:

Следовательно, за время равноускоренного вращения маховик успеет совершить 180 оборотов.

5. Прежде чем найти по формуле

скорость точек на ободе маховика в момент времени t=45 сек после начала равноускоренного вращения, необходимо найти угловую скорость маховика 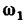в этот момент:

Зная, что 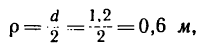получаем

Решение 2—угловые величины выражаются в оборотах, а время — в сек (t=1,5 мин — 90 сек).

1. Выражаем данные угловые скорости в об/сек.

2. Представим формулу (3) в ином виде, приняв
Тогда

3. Обозначив 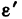—угловое ускорение, выраженное через обороты, формулу (2) можно представить в виде

и тогда

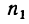
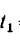
4. Найдем — угловую скорость маховика через = 45 сек после начала равноускоренного вращения:

что соответствует

Теперь находим при этой угловой скорости маховика скорость точек на его ободе:

Если же 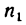выражено в об/сек, то

Задачу можно решить и не переводя заданное время из минут в секунды, т. е. решить при заданных числовых величинах

Этот вариант решения рекомендуем выполнить самостоятельно

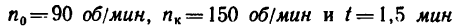
Задача №2

Вал, вращающийся равноускоренно из состояния покоя, в первые 12 сек совершает 95,5 оборота. С каким угловым ускорением вращается вал и какую угловую скорость он приобретает?

Решение.

1. Угловое перемещение за время t=12 сек равноускоренного движения составляет

2. Из формулы (5) находим угловое ускорение вала:

3. К концу 12-й секунды вал приобретает угловую скорость [см. формулу (6)):

что соответствует

Задачу можно решить и в другой последовательности, а также выражая величины через обороты.

Задача №3

Колесо, вращающееся со скоростью 1500 об/мин, при торможении начинает вращаться равнозамедленно и через 30 сек останавливается. Определить угловое ускорение и число оборотов колеса с момента начала торможения до остановки.

Решение.

1. Выразим начальную угловую скорость в рад/сек:

Найдем угловое ускорение из формулы (2):

2. Представим формулу (3) в виде

Тогда число оборотов вала за t = 30 сек — 0,5 мин

Неравномерное вращательное движение
Плоскопараллельное движение тела
Определение передаточных отношений различных передач
Задачи на поступательное движение тела
Неравномерное движение точки по любой траектории
Определение траектории, скорости и ускорения точки
Кинематический способ определения радиуса кривизны траектории
Равномерное вращательное движение

Источник

Вращением твердого тела вокруг неподвижной оси называется такое движение твердого тела, при котором хотя бы две его точки остаются неподвижными.

Прямая, проходящая через эти неподвижные точки называется осью вращения.

Траекториями движения точек твердого тела являются окружности с радиусами равными расстояниям от заданных точек тела до оси вращения.

Уравнение вращательного движения твердого тела.

Уравнение вида , где phi (t) — угол поворота тела вокруг оси, является законом вращения твердого тела, так как определяет положение точки на траектории в любой момент времени.

Если ось вращения совпадает с осью , то величина ${omega _z} = frac{{dphi }}{{dt}}$ называется модулем угловой скорости. Вектор угловой скорости ${vec omega _z} = frac{{dphi }}{{dt}}vec k$ направлен вдоль оси вращения.

Величина ${vec varepsilon _z} = frac{{d{omega _z}}}{{dt}}vec k$ называется угловым ускорением.

Частные случаи вращательного движения твердого тела.

Если ${omega _z} > 0$ , то вращение происходит в положительном направлении (против движения часовой стрелки);
Если ${omega _z} < 0$ , то вращение происходит в отрицательном направлении (в направлении движения часовой стрелки);
Если ${omega _z}$ и ${varepsilon _z}$ имеют одинаковые знаки, то вращение является ускоренным;
Если ${omega _z}$ и ${varepsilon _z}$ имеют разные знаки, то вращение является замедленным;
Если ${omega _z} = const$ , то ${varepsilon _z} = 0$ и вращение является равномерным;
Если ${varepsilon _z} = const$ , то вращение является равноускоренным (или равнозамедленным).

Скорости и ускорения точек вращающегося твердого тел

При вращении твердого тела все его точки движутся по своим окружностям, центры которых лежат на оси вращения.

Пусть произвольная точка ${M_i}$ движется вокруг оси вращения по окружности радиуса ${h_i}$ с угловой скоростью omega . В соответствие с формулой Эйлера (К.12) для движения точки по окружности можно определить линейную скорость движения точки

${v_i} = {h_i} cdot omega$ .

Запишем также модули касательной и нормальной компоненты ускорения точки ${M_i}$ .

Касательное ускорение ${a_{{tau _i}}} = frac{{d{v_i}}}{{dt}} = {h_i}frac{{domega }}{{dt}} = {h_i}varepsilon$ .

Нормальное ускорение. Так как радиус кривизны окружности rho равен радиусу окружности ${h_i}$ , то при движении по окружности $rho = {h_i}$ . В этом случае ${a_{{n_i}}} = frac{{{v_i}^2}}{rho } = frac{{{h_i}^2{omega ^2}}}{{{h_i}}} = {h_i}{omega ^2}$ .

Полное ускорение. ${a_i} = sqrt {a_{{tau _i}}^2 + a_{{n_i}}^2} = {h_i}sqrt {{varepsilon ^2} + {omega ^4}}$ .

Пример.

Вал, делающий n = 90 об/мин после выключения двигателя начинает вращаться равнозамедленно и останавливается через .

Определить число оборотов вала до остановки.

Решение.

Начальная угловая скорость ${omega _0} = frac{{2pi n}}{{60}} = frac{{180pi }}{{60}}$ .

Поскольку вал вращается равнозамедленно, то $frac{{domega }}{{dt}} = {varepsilon _0} = const$ . Интегрируя последнее уравнение, получим $omega = {varepsilon _0}t + {c_1}$ , где ${c_1}$ — константа интегрирования.

Определим константу интегрирования ${c_1}$ . При t = 0 угловая скорость $omega = {omega _0}$ , поэтому $omega = {varepsilon _0}t + {omega _0}$ или $frac{{dphi }}{{dt}} = {varepsilon _0}t + {omega _0}$ . Интегрируя последнее уравнение, получим $phi = frac{{{varepsilon _0}{t^2}}}{2} + {omega _0}t + {c_2}$ . Будем считать, что при t = 0 начальный угол ${phi _0} = 0$ . (Этого всегда можно добиться соответствующим выбором системы отсчета). Тогда $phi = frac{{{varepsilon _0}{t^2}}}{2} + {omega _0}t$ .

Конечная угловая скорость ${omega _1}$ при t = T равна нулю, то есть ${omega _1} = 0$ . Следовательно, ${varepsilon _0}T + {omega _0} = 0$ (*).

Конечный угол поворота ${phi _1}$ равен ${phi _1} = frac{{{varepsilon _0}{T^2}}}{2} + {omega _0}T$ (**). Тогда с учетом (*) можно записать ${phi _1} = - frac{{{omega _0}T}}{2} + {omega _0}T = frac{{{omega _0}T}}{2} = frac{{180pi }}{{2 cdot 60}}40 = frac{{180pi }}{3}$ .

Поскольку один оборот 2pi равен радиан, число оборотов вала до остановки равно $N = frac{{{phi _1}}}{{2pi }} = 30$ об.

Пример. Вал начинает вращаться равноускоренно из состояния покоя. В первые 5 c он совершает 12.5 оборотов. Какова угловая скорость по истечении 5 секунд?

Дано.

В начальный момент времени при t = 0 начальный угол и начальная угловая скорость равны нулю, то есть ${omega _0} = 0$ и ${phi _0} = 0$ . Время вращения T = 5 c . За это время вал повернулся на угол ${phi _1} = 12.5 cdot 2pi = 25pi$ (радиан).

Решение. Вал вращается равноускоренно, поэтому ${varepsilon _0} = const$ , следовательно $frac{{domega }}{{dt}} = {varepsilon _0}$ или $domega = {varepsilon _0}dt$ . Интегрируя последнее равенство, получим $omega = {varepsilon _0}t + {c_1}$ , где ${c_1}$ — константа интегрирования.

Определим константу интегрирования ${c_1}$ . При t = 0 начальная угловая скорость , поэтому $omega = {varepsilon _0}t$ (*) или $frac{{dphi }}{{dt}} = {varepsilon _0}t$ или $dphi = {varepsilon _0}tdt$ . Интегрируя последнее уравнение, получим $phi = frac{{{varepsilon _0}{t^2}}}{2} + {c_2}$ . Будем считать, что при t = 0 начальный угол ${phi _0} = 0$ . (Этого всегда можно добиться соответствующим выбором системы отсчета). Тогда $phi = frac{{{varepsilon _0}{t^2}}}{2}$ .

Нам из условия задачи известно, что конечный угол поворота ${phi _1}$ равен ${phi _1} = frac{{{varepsilon _0}{T^2}}}{2} = 25pi$ (**). Тогда можно определить угловое ускорение ${varepsilon _0} = frac{{2 cdot 25pi }}{{{T^2}}} = 2pi$ .

Теперь из уравнения (*) можно определить искомую угловую скорость при t = T : (1/сек).

Источник

Скачать материал

Сейчас обучается 389 человек из 62 регионов

Сейчас обучается 268 человек из 65 регионов

Описание презентации по отдельным слайдам:

17 слайд

1. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения Мтр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском.
Дано:
I = 245 кг·м2
= 20 об/c
t = 1 мин

Mтр — ?
N — ?
Решение
Запишем уравнение основного закона динамики вращательного движения:
В проекциях на ось OX:
Отсюда проекция вектора углового ускорения на ось OX:
Величина углового ускорения постоянна, векторы углового ускорения и угловой скорости направлены противоположно. Проекция угловой скорости колеса на ось OX:
18 слайд

Колесо остановится, поэтому
Решение (продолжение)
Величина (модуль) вектора углового ускорения:
1. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения Мтр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском.
Для модулей векторов:
19 слайд

Величина углового перемещения колеса изменяется как
Решение (продолжение)
Из двух кинематических уравнений движения получаем систему уравнений:
Величину углового ускорения ε получим из второго уравнения и подставим в первое:
1. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения Мтр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском.
20 слайд

1. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения Мтр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском.
Решение (продолжение)
Величину углового перемещения φ выразим через число оборотов, сделанных до остановки, а начальную угловую скорость – через начальную частоту вращения:
После подстановки получим:
Отсюда полное число оборотов колеса до остановки:
Ответ: Мтр = 513 H·м, N = 600.
21 слайд

5. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса.
Дано:
I = 245 кг·м2
= 20 об/c
N = 1000

Mтр — ?
t — ?
Решение
Запишем уравнение основного закона динамики вращательного движения:
В проекциях на ось OX:
Отсюда проекция вектора углового ускорения на ось OX:
Величина углового ускорения постоянна, векторы углового ускорения и угловой скорости направлены противоположно. Угловое перемещение колеса
22 слайд

5. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса.
Величина угловой скорости колеса изменяется как
Колесо остановится, поэтому
Решение (продолжение)
Из двух кинематических уравнений движения получаем систему уравнений:
Величину углового ускорения ε получим из второго уравнения и подставим в первое:
23 слайд

5. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса.
Величину углового перемещения φ выразим через число оборотов, сделанных до остановки, а начальную угловую скорость – через начальную частоту вращения:
Решение (продолжение)
После подстановки получим:
Откуда время движения до остановки:
24 слайд

5. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса.
Решение (продолжение)
Теперь вернёмся к динамическому уравнению движения и найдём величину момента сил трения. Для проекций на ось OX:
Величина момента сил трения
Или, для краткости,
Как было получено ранее,
Теперь
25 слайд

5. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса.
Решение (продолжение)
Ответ: t = 100 c; Мтр = 308 H·м.
26 слайд

2. На барабан радиусом R = 20 см, момент инерции которого I = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом h0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Ек груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь.
Дано:
m = 0,5 кг
I = 0,1 кг·м2
R = 20 cм
h0 = 1 м

t — ?
Ек — ?
Т — ?
Решение
Прежде всего, запишем динамическое уравнение движения груза. Из второго закона Ньютона:
Для проекций на ось OY:
Если учесть, что груз опускается, то
где a — величина (модуль) проекции ускорения на ось OY.
a = const., начальная скорость груза равна нулю, следовательно кинематическое уравнение движения можно записать так:
27 слайд

2. На барабан радиусом R = 20 см, момент инерции которого I = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом h0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Ек груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь.
Решение (продолжение)
Через время t груз окажется на земле (y = 0), поэтому
Величину ускорения можно определить из уравнения второго закона Ньютона
но для этого нужно знать величину силы натяжения нити T.
Запишем уравнение основного закона динамики вращательного движения для барабана:
В проекциях на ось OZ, перпендикулярную плоскости рисунка:
Из третьего закона Ньютона
28 слайд

2. На барабан радиусом R = 20 см, момент инерции которого I = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом h0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Ек груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь.
Решение (продолжение)
Величину углового ускорения ε можно выразить через величину линейного ускорения a:
Теперь можно записать систему уравнений, из которой можно определить a и T:
29 слайд

2. На барабан радиусом R = 20 см, момент инерции которого I = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом h0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Ек груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь.
Решение (продолжение)
Найдём величину линейного ускорения a:
Подставим выражение для a в формулу для времени движения груза:
30 слайд

2. На барабан радиусом R = 20 см, момент инерции которого I = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом h0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Ек груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь.
Ответ: t = 1,1 c; Ek = 0,82 Дж; Т = 4,1 H.
Решение (продолжение)
Кинетическая энергия груза
Скорость груза
где
31 слайд

3. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что блок вращается с угловым ускорением  = 2,36 рад/c2. Блок считать однородным диском.
Дано:
Mтр = 98,1 Н·м
I = 50 кг·м2
R = 20 cм
e = 2,36 рад/c2

Т2 – Т1 — ?
Решение
Вращательное движение блока описывается основным законом динамики вращательного движения.
Запишем для блока:
Для проекций на ось OZ, направленную перпендикулярно плоскости рисунка.
Согласно третьему закону Ньютона
32 слайд

3. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т1 – Т2 по обе стороны блока, если известно, что блок вращается с угловым ускорением  = 2,36 рад/c2. Блок считать однородным диском.
Решение (продолжение)
Из этого уравнения получаем:
Ответ: T2 – T21 =1,08 кН.
33 слайд

3А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что массы гирь m1 = 1 кг, m2 = 1,5 кг. Блок считать однородным диском.
Дано:
Mтр = 98,1 Н·м
I = 50 кг·м2
R = 20 cм
m1 = 1 кг
m2 = 1,5 кг

Т2 – Т1 — ?
Решение
Поступательное движение гирь описывается вторым законом Ньютона, а вращательное движение блока – основным законом динамики вращательного движения.
Запишем для гирь и блока:
Перепишем систему уравнений. Для этого первое и второе уравнения запишем для проекций на вертикальную ось OY, а третье – для проекций на ось OZ, направленную перпендикулярно плоскости рисунка.
34 слайд

Решение (продолжение)
Согласно третьему закону Ньютона
Величину углового ускорения ε можно выразить через величину линейного ускорения a:
Нить нерастяжима, поэтому
3А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что массы гирь m1 = 1 кг, m2 = 1,5 кг. Блок считать однородным диском.
35 слайд

Решение (продолжение)
Система уравнений приобретает вид:
Вычтем из второго уравнения первое и выполним элементарные преобразования в третьем:
3А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что массы гирь m1 = 1 кг, m2 = 1,5 кг. Блок считать однородным диском.
36 слайд

Решение (продолжение)
3А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что массы гирь m1 = 1 кг, m2 = 1,5 кг. Блок считать однородным диском.
Разделим первое уравнение на второе:
37 слайд

Решение (продолжение)
3А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что массы гирь m1 = 1 кг, m2 = 1,5 кг. Блок считать однородным диском.
38 слайд

4. Найти линейные скорости  движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0,5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
Решение
Дано:
h = 0,5 м
0 = 0

v — ?
Задачу решим с помощью закона сохранения энергии. Любое из трёх перечисленных в условии тел участвует в двух движениях – поступательном с скоростью v и вращательном вокруг своего центра масс. Поэтому кинетическая энергия тела складывается из кинетической энергии поступательного движения и кинетической энергии вращательного движения.
В системе действуют только консервативные силы (трения нет), поэтому изменение полной механической энергии равно нулю.
39 слайд

4. Найти линейные скорости  движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0,5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
Решение (продолжение)
потенциальная энергия тела в поле силы тяжести уменьшилась.
кинетическая энергия поступательного движения тела увеличилась.
кинетическая энергия вращательного движения тела увеличилась. Здесь ω — угловая скорость вращения тела.
40 слайд

4. Найти линейные скорости  движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0,5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
Решение (продолжение)
Любое из тел катится без проскальзывания, поэтому
По этой общей формуле можно найти скорость любого из трёх тел, для этого достаточно подставить выражение для момента инерции соответствующего тела.
41 слайд

4. Найти линейные скорости  движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0,5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
Решение (продолжение)
1. Шар:
2. Диск:
42 слайд

4. Найти линейные скорости  движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0,5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
Ответ: 1 = 2,65 м/c, 2 = 2,56 м/c, 3 = 2,21 м/c;  = 3,13 м/c.
Решение (продолжение)
3. Обруч:
4. Для тела, соскальзывающего без вращения по наклонной плоскости
43 слайд

6. Маховое колесо начинает вращаться с угловым ускорением  = 0,5 рад/c2 и через время t1 = 15 с после начала движения приобретает момент импульса L1 = 73,5 кгм2/c. Найти кинетическую энергию T колеса через время t2 = 20 с после начала движения.
Решение
Дано:
 = 0,5 рад/c2
ω0 = 0
t1 = 15 с
t2 = 20 с
L1 = 73,5 кгм2/c

Т — ?
Кинетическую энергию вращающегося колеса можно найти как
где I – момент инерции колеса, ω2 – угловая скорость колеса в момент времени t2.
Колесо вращается равноускоренно, начальная угловая скорость вращения равна нулю.
Величина (модуль) момента импульса колеса
Отсюда
44 слайд

6. Маховое колесо начинает вращаться с угловым ускорением  = 0,5 рад/c2 и через время t1 = 15 с после начала движения приобретает момент импульса L1 = 73,5 кгм2/c. Найти кинетическую энергию T колеса через время t2 = 20 с после начала движения.
Ответ: T=490 Дж.
Решение (продолжение)
Подставим в формулу для кинетической энергии полученные выражения для момента инерции и угловой скорости.
45 слайд

7. К ободу диска массой m = 5 кг приложена касательная сила F = 19,6 Н. Какую кинетическую энергию T будет иметь диск через время t = 5 с после начала действия силы?
Решение
Дано:
m = 5 кг
ω0 = 0
t = 5 с
F = 19,6 Н

Т — ?
Кинетическую энергию вращающегося диска можно найти как
где I – момент инерции диска, ω – угловая скорость колеса в момент времени t.
Сила F создаёт постоянный вращающий момент, что приводит к равноускоренному вращению диска. Основной закон динамики вращательного движения можно записать так:
Для проекций на ось OX (см. рисунок):
Диск вращается равноускоренно, начальная угловая скорость вращения равна нулю,
46 слайд

7. К ободу диска массой m = 5 кг приложена касательная сила F = 19,6 Н. Какую кинетическую энергию T будет иметь диск через время t = 5 с после начала действия силы?
Ответ: T=1,92 кДж.
Решение (продолжение)
Момент инерции диска относительно данной оси вращения
47 слайд

8. Однородный стержень длиной l = 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую минимальную скорость  надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?
Дано:
l = 85 см

v — ?
Решение
Если мы сообщим нижнему концу стержня некоторую скорость, он сможет совершить полный оборот вокруг оси, проходящей через точку О.
Если эта скорость минимальная из всех возможных, при которых стержень совершит оборот, то в верхней точке скорость стержня будет очень близка к нулю (рис. 2).
Для определения минимальной скорости, при которой возможен полный оборот стержня применим закон сохранения энергии. Трение в системе отсутствует, поэтому можно считать, что все силы, действующие в системе консервативны.
Изменение потенциальной энергии в поле сил тяжести определим по изменению положения центра тяжести стержня, который совпадает с его геометрическим центром.
48 слайд

8. Однородный стержень длиной l = 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую минимальную скорость  надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?
Решение (продолжение)
Потенциальная энергия стержня в поле сил тяжести увеличилась.
Кинетическая энергия стержня уменьшилась, так как в верхней точке он практически остановился.
Здесь ω — начальная угловая скорость стержня.
Момент инерции стержня относительно точки O
49 слайд

8. Однородный стержень длиной l = 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую минимальную скорость  надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?
Ответ: =7,1 м/c.
Решение (продолжение)
50 слайд

9. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 1 = 10 об/мин. Человек массой m0 = 60 кг стоит при этом на краю платформы. С какой частотой 2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека  точечной массой. Трения нет.
Решение
Дано:
m = 100 кг
m0 = 60 кг
n1 = 10 об/мин

n2 — ?
На рассматриваемую систему не действуют внешние моменты сил, следовательно её момент импульса сохраняется.
Направлены моменты импульса системы одинаково. Для проекций на вертикальную ось OZ:
В случае, когда человек стоит на краю платформы, момент инерции системы
51 слайд

9. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 1 = 10 об/мин. Человек массой m0 = 60 кг стоит при этом на краю платформы. С какой частотой 2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека  точечной массой. Трения нет.
В случае, когда человек стоит в центре платформы, его момент инерции относительно рассматриваемой оси равен нулю, а момент инерции системы
Решение (продолжение)
Подставим выражения для моментов инерции в закон сохранения момента импульса:
Угловая скорость связана с частотой вращения соотношением:
52 слайд

9. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 1 = 10 об/мин. Человек массой m0 = 60 кг стоит при этом на краю платформы. С какой частотой 2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека  точечной массой. Трения нет.
Ответ: 2 = 22 об/мин.
Решение (продолжение)
53 слайд

10. Горизонтальная платформа массой m = 80 кг и радиусом R = 1 м вращается с частотой 1 = 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I1 = 2,94 кг·м2 до I2 = 0,98 кгм2? Считать платформу однородным диском. Трения нет.
Решение
Дано:
m = 80 кг
R = 1 м
 1 = 20 об/мин
I1=2,94 кгм2
I2=0,98 кгм2

n2 — ?
На рассматриваемую систему не действуют внешние моменты сил, следовательно её момент импульса сохраняется.
Направлены моменты импульса системы одинаково. Для проекций на вертикальную ось OZ:
Угловая скорость связана с частотой вращения соотношением:
54 слайд

10. Горизонтальная платформа массой m=80 кг и радиусом R=1 м вращается с частотой 1=20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I1=2,94 кгм2 до I2=0,98 кгм2? Считать платформу однородным диском. Трения нет.
Решение (продолжение)
Частота вращения после изменения момента инерции
Момент инерции системы
Момент инерции диска
55 слайд

10. Горизонтальная платформа массой m = 80 кг и радиусом R = 1 м вращается с частотой 1 = 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I1 = 2,94 кг·м2 до I2 = 0,98 кгм2? Считать платформу однородным диском. Трения нет.
Ответ: 2=21 об/мин.
Решение (продолжение)
56 слайд

11. Человек массой m0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой  будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека  точечной массой. Трения нет.
Решение
Дано:
m0 = 60 кг
m = 100 кг
0 = 4 км/ч
R = 10 м

n — ?
На рассматриваемую систему не действуют внешние моменты сил, следовательно её момент импульса сохраняется.
В лабораторной системе отсчёта
— момент импульса системы до начала движения человека;
— момент импульса системы после начала движения человека.
В лабораторной системе отсчёта
— момент импульса платформы;
— момент импульса человека.
57 слайд

Решение (продолжение)
Направлены моменты импульса человека и платформы в противоположные стороны. Для проекций на вертикальную ось OZ:
В уравнение входит величина проекции скорости человека в лабораторной системе отсчёта, а в условии дана скорость относительно платформы. Найдём величину скорости в лабораторноё системе отсчёта.
Как только человек начнёт движение, платформа начнёт вращаться в противоположном направлении (см. рисунок). Поэтому по закону сложения скоростей
Величина линейной скорости края платформы
11. Человек массой m0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой  будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека  точечной массой. Трения нет.
58 слайд

Решение (продолжение)
Величина линейной скорости человека в лабораторной системе отсчёта
Подставим выражение для величины линейной скорости человека в лабораторной системе отсчёта в уравнение закона сохранения момента импульса:
Теперь осталось определить угловую скорость вращения платформы из последнего уравнения.
11. Человек массой m0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой  будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека  точечной массой. Трения нет.
59 слайд

Решение (продолжение)
Напомним, что I – момент инерции платформы, которая имеет форму диска.
11. Человек массой m0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой  будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека  точечной массой. Трения нет.
60 слайд

Ответ:  = 3,6 об/мин.
Решение (продолжение)
Угловая скорость связана с частотой вращения соотношением:
11. Человек массой m0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой  будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека  точечной массой. Трения нет.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 263 262 материала в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

04.12.2020
169
0

19.11.2020
575
0

10.11.2020
787
14

24.10.2020
1909
31

15.10.2020
161
1

15.08.2020
115
0

03.07.2020
2331
34

26.04.2020
924
7

Вам будут интересны эти курсы:

Курс профессиональной переподготовки «Маркетинг: теория и методика обучения в образовательной организации»
Курс повышения квалификации «Экономика и право: налоги и налогообложение»
Курс повышения квалификации «Введение в сетевые технологии»
Курс повышения квалификации «Специфика преподавания конституционного права с учетом реализации ФГОС»
Курс повышения квалификации «История и философия науки в условиях реализации ФГОС ВО»
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС технических направлений подготовки»
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
Курс повышения квалификации «Организация маркетинга в туризме»
Курс профессиональной переподготовки «Организация деятельности помощника-референта руководителя со знанием иностранных языков»
Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»
Курс профессиональной переподготовки «Информационная поддержка бизнес-процессов в организации»

Источник

сколько оборотов совершит тело до остановки

Описание презентации по отдельным слайдам:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Другие материалы

Вам будут интересны эти курсы:

Не пропустите также: