Как правильно рассчитать концентрацию ионов водорода и рН в растворе серной кислоты
Задача 101.
Вычислите [Н+] и рН 0,01 М и 0,05 Н растворов Н2SO4.
Решение:
CM(Н2SO4) = 0,01 М;
CH(Н2SO4) = 0,05 М;
a) Вычисление [Н+] и рН 0,01 М раствора Н2SO4
Так как Н2SO4 двухосновная кислота и является сильным электролитом, то концентрация ионов водорода будет равна удвоенному значению ее молярности.
[Н+] = 2СМ(Н2SO4) = (2 · 0,01) = 2 · 10-2 моль/дм3;
рН = -lg[Н+] = -lg2 · 10-2 = 2 — lg2 = 2 — 0,30 = 1,70.
б) Вычисление [Н+] и рН 0,05 Н раствора Н2SO4
Так как Н2SO4 двухосновная кислота и является сильным электролитом, то концентрация ионов водорода будет равна ее нормальности.
[Н+] = СН(Н2SO4) = (1 · 0,05) = 5 · 10-2 моль/дм3;
рН = -lg[Н+] = -lg5 · 10-2 = 2 — lg5 = 2 — 0,70 = 1,30.
Ответ: а) [Н+] = 2 · 10–2 моль/дм3; рН = 1,70; б) [Н+] = 5 · 10–2 моль/дм3; рН = 1,30.
Задача 102.
Вычислите [Н+] и рН раствора Н2SO4 с массовой долей кислоты 0,5% (р = 1,00 г/см3).
Решение:
М(Н2SO4) = 98 г/моль;
w% = 0,5% или 0,005;
р = 1,00 г/см3.
1. Рассчитаем молярность раствора кислоты
CM(Н2SO4) = (w% · p · 1000)/М(Н2SO4) = (0,005 · 1,00 г/см3 · 1000 cм3)/98 г/моль = 0,05 M.
Так как Н2SO4 двухосновная кислота и является сильным электролитом, то концентрация ионов водорода будет равна удвоенному значению ее молярности.
[Н+] = 2СМ(Н2SO4) = (2 · 0,05) = 1 · 10-1 моль/дм3;
рН = -lg[Н+] = -lg1 · 10-1 = 1 — lg2 = 1 — 0,00 = 1,00.
Ответ: [Н+] = 0,1 моль/дм3;рН = 1,00.
Задача 103.
Вычислите [Н+] и рН 0,5 М раствора гидроксида аммония.
Решение:
КD(NH4OH) = 1,76 · 10–5;
CM(NH4OH) = 0,5 М.
Схема диссоциации NH4OH:
NH4OH ⇔ NН4+ + OH–
Поскольку КD(NH4OH) << CM(NH4OH) так как (1,76 · 10–5) << 0,5, то можно считать, что равновесная концентрация недиссоциированного основания равна его общей концентрации: СМ(NH4OH) = 0,5 моль/дм3.
Для слабых оснований [H+] вычисляют по формуле:
рН = -lg[Н+] = -lg3,37 · 10-12 = 12 — lg3,37 = 12 — 0,53 = 11,47.
Ответ: [Н+] = 3,37 · 10–12 моль/дм3;рН = 11,47.
Расчет концентрации ионов в растворе одного вещества
Концентрация
ионов определяется степенью диссоциации
()
и молярной концентрацией вещества (См).
Случай
А. Сильные электролиты
Здесь
достаточно хорошим приближением является
= 1, т.е. все молекулы полностью диссоциированы
на ионы.
Пример
1
Рассчитать
концентрацию всех ионов в 1 М растворе
Al2(SO4)3.
Решение
Al2(SO4)3
— соль, т. е. сильный электролит. Она
диссоциирует в одну ступень нацело и
необратимо:
Al2(SO4)3
2Al3+
+ 3SO42-.
Из
уравнения диссоциации видно, что из
одной молекулы соли образуются 2 иона
алюминия и 3 сульфат-иона
[Al3+]=2Cм
= 2 моль/л; [SO42-]=
3См
= 3 моль/л.
Пример
2
Рассчитать
рН 0.1 М раствора NaOH.
Решение
Гидроксид
натрия — щелочь (сильное основание),
следовательно, диссоциирует необратимо
и полностью:
NaOH
Na++OH—
;
при
диссоциации из его одной молекулы
образуется один гидроксид-ион,
следовательно,
[OH—]=
См = 0.1 моль/л,
рОН
= — lg
[OH—]=
1,
pH=
14- рОН = 13.
Случай
В. Несильные электролиты
Соли,
как правило, являются сильными
электролитами, поэтому этот случай
относится к несильным кислотам и
основаниям.
Пример
3
Рассчитать
концентрацию всех ионов в 0.2 М растворе
сернистой кислоты и ее степень диссоциации
по первой и второй ступеням.
Решение
Здесь
,
диссоциация обратима:
первая
ступень H2SO3
HSO3—
+ H+,
Ка1=
[HSO3—][H+]/[H2SO3]=
1.610-2
; (1)
вторая
ступень HSO3—
SO32-
+ H+,
Ka2=
[SO32-][H+]/[HSO3—]=
6.310-8
. (2)
Из
уравнений диссоциации следует, что
образование одного иона HSO3—
сопровождается образованием одного
иона H+,
а образование одного иона SO32-
сопровождается образованием двух H+,
следовательно, концентрации всех ионов
связаны уравнением
[HSO3—]+
2[SO32-]=
[H+],
(3)
а
равновесная концентрация кислоты
определяется уравнением
[H2SO3]=
Cм
— [HSO3—]-
[SO32-].
(4)
Решая
систему уравнений (1)-(4) можно рассчитать
концентрации всех ионов, однако следует
обратить внимание на то, что Ka1Ka2.
Отсюда следует, что концентрации ионов
Н+
и HSO3—
определяются, главным образом, диссоциацией
по первой ступени. Вторая ступень
диссоциации играет главную роль лишь
в образовании ионов SO32-.
Расчет
[Н+],
[HSO3—]
и [H2
SO3]
Из
уравнения (1) следует, что при распаде
одной молекулы кислоты образуется один
ион Н+
и один ион HSO3—,
следовательно, концентрации этих ионов
равны х = [Н+]
= [HSO3-2],
а равновесная концентрация [H2
SO3]=
См — х.. Подставляя эти выражения в закон
действия масс для первой ступени, получим
Ка1=
х2
/(См — х)= 1.610-2
или
х2
/(0.2- х)= 1.610-2,
откуда
х1
= -6.510-2
и х2
= 4.910-2.
Концентрация не может быть отрицательной
величиной, поэтому решением является
второй корень уравнения. Окончательно
можно записать
[Н+]
= [HSO3—]
= 4.910-2
моль/л, [H2
SO3]=
0.151 моль/л,
1
= [Н+]/См
= 4.910-2
моль/л/0.2 моль/л = 0.245, или 24.5%.
Расчет
[SO32-]
Из
равенства значений [Н+]
и [HSO3—]
в соответствии с уравнением (2) следует
[SO32-][H+]/[HSO3—]=
[SO32-]
= Ка2
= 6.310-8
моль/л,
2
= [SO32-]/[HSO3—]=
6.310-8
моль/л./ 4.910-2
моль/л = 1.29 10-6.
ВЫВОД:
при расчете рН растворов слабых
электролитов достаточно рассмотреть
первую ступень диссоциации.
Пример
4
Рассчитать
степень диссоциации гидроксида аммония
и рН его 5%- раствора (плотность раствора
=0.97
г/мл).
Решение
1).
Для решения задачи необходимо знать
молярную концентрацию вещества. Для ее
расчета удобно исходить из 1 литра
раствора:
его
масса mp=
V
= 1000 мл0.97
г/мл = 970 г;
масса
растворенного вещества m=
mp
= 970 г0.05
= 48.5 г;
количество
растворенного вещества =
m/М
= 48.5 г/35г/моль =1.39 моль;
молярная
концентрация См=/
V=
1.39 моль/1 л = 1.39 моль/л.
2).
Рассмотрим равновесие:
NH4OH
NH4+
+
OH—.
Кв=
[NH4+][OH—]/[NH4OH]=
1.810-5
.
Воспользуемся
законом разбавления Оствальда
=
(К/См)
= =(1.810-5
/1.39) = 3.6 10-3
;
1,
следовательно, применение этого закона
допустимо. При диссоциации одной молекулы
исходного вещества образуется 1 ион
ОН—;
в одном литре раствора диссоциирует
См
молекул, следовательно, образуется
столько же ионов ОН—,
тогда
[ОН—]=
См
=3.6 10-3
1.39 моль/л = 5.0010-3
моль/л,
рОН
= — lg[ОН—]
= — lg
5.0010-3
= 2.30,
pH
= 14-pOH=
14 -2.30 = 11.70.
Замечание:
если результатом расчета по закону
разбавления оказывается, что
0.1, то для расчета
необходимо воспользоваться более точным
уравнением К=2См/(1-)
или сначала рассчитать равновесные
концентрации ионов (см. пример 3), а затем
..
Соседние файлы в предмете Химия
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Серная кислота является сильной неорганической кислотой, обычно используемой в промышленном производстве химических веществ, в исследовательской работе и в лабораторных условиях. Имеет молекулярную формулу H2SO4. Он растворим в воде при любых концентрациях с образованием раствора серной кислоты. В растворе моль серной кислоты разделяется на моль отрицательно заряженных сульфат-ионов, или SO 4 (2-), и 2 моль положительно заряженных ионов гидрония, или H 3 O +. Концентрация этих ионов выражается в молярности, которая определяется как число молей ионов на литр раствора. Их концентрация зависит от начальной концентрации серной кислоты.
Определение ионных концентраций
-
Предположение о том, что серная кислота полностью растворяется в воде, справедливо, поскольку серная кислота является сильной кислотой, а полное растворение в воде является характеристикой сильных кислот. Дополнительные шаги необходимы для расчета концентрации ионов в растворе для слабой кислоты.
-
Всегда соблюдайте правила техники безопасности в лаборатории или в любое время при работе с кислотами. Это включает в себя использование защитного оборудования, такого как лабораторные халаты, защитные очки, перчатки и соответствующую стеклянную посуду.
••• ollaweila / iStock / Getty Images
Запишите сбалансированное уравнение для растворения или диссоциации серной кислоты в воде. Сбалансированное уравнение должно быть: H2SO4 + 2H2O -> 2H3O + + SO4 (2-). Уравнение показывает, что для растворения одного моля серной кислоты в воде в реакции образуется 2 моля ионов гидрония и 1 молей сульфат-ионов. Для раствора серной кислоты с начальной концентрацией 0, 01 моль это означает, что в 1 л раствора содержится 0, 01 моль серной кислоты.
Умножьте начальные концентрации кислоты на их коэффициенты, чтобы определить индивидуальные концентрации ионов. Коэффициенты — это числа перед формулами в сбалансированном химическом уравнении. Формулы без чисел перед ними имеют коэффициент 1. Это будет означать, что начальная концентрация кислоты умножается на 1, чтобы определить молярность сульфат-ионов в растворе; 1 х 0, 01 моль = 0, 01 моль SO4 (2-). Начальную концентрацию умножают на 2, чтобы определить концентрацию ионов гидрония в растворе; 2 х 0, 01 моль = 0, 02 моль H3O +.
Умножьте начальную концентрацию кислоты на 3, чтобы определить общую концентрацию ионов в 0, 01-мольном растворе серной кислоты. Поскольку один моль кислоты продуцирует в общей сложности 3 моля ионов, общая ионная концентрация составляет 3 × 0, 01 моля = 0, 03 моля ионов.
подсказки
Предупреждения
Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований
В практике аналитической химии широко используются кислотно-основные реакции для разделения, растворения, определения ионов, создания условий для взаимодействия частиц в растворе и др. Поэтому необходимо научиться рассчитывать равновесные концентрации ионов ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-581.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-582.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-583.png)
Константа автопротолиза растворителя ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-585.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-586.png)
для воды ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-587.png)
для метанола
Учитывая, что активность чистого растворителя (стандартное состояние вещества) равна 1, справедливы выражения:
(в чистой воде ионная сила I мала, близки к 1);
При расчетах, связанных с кислотно-основным равновесием и кислотно-основными взаимодействиями в растворах слабых протолитов, считают табличные термодинамические значения констант ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-592.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-593.png)
В качестве характеристик кислотности используются отрицательные десятичные логарифмы активности (при приближенных расчетах без учета ионной силы — логарифмы концентрации) ионов лиония и лиата (для воды ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-594.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-595.png)
Для воды:
Соответственно: ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-598.png)
В чистой воде, нейтральном водном растворе:
Для метанола (см. также пример 3.7):
и нейтральному раствору в метаноле соответствует pH = 8,35.
Эти соотношения используют для вычисления равновесной концентрации одного из ионов растворителя, если концентрация другого известна.
При описании поведения сильных и слабых кислот и оснований следует помнить о том, что сильные протолиты в водных растворах диссоциируют практически полностью, степень диссоциации (ионизации) ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-602.png)
или (в упрощенном виде):
Из реакций следует, что для одноосновных протолитов в воде справедливо:
Если НА и В — кислотно-основная сопряженная пара и В соответствует ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-608.png)
а для растворителя
При растворении в воде солей, в состав которых входит анион слабой кислоты (![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-611.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-612.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-613.png)
Реакция гидролиза характеризуется константой равновесия, соответствующей протолитыческому поведению гидролизующейся частицы ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-614.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-615.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-616.png)
Например, для соли ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-617.png)
Для соли с катионом слабого основания, например ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-620.png)
(поскольку для сопряженных протолитов в воде ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-622.png)
Для соли, в которой и катион, и анион — ионы слабых протолитов, например
(протекает гидролиз “по катиону» и “по аниону”, среда зависит от ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-625.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-626.png)
Для кислой соли с катионом сильного основания, например ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-628.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-629.png)
(упрощенно: 2) ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-631.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-632.png)
Для реакции 1)
для реакции 2)
От соотношения ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-635.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-636.png)
Заменяя концентрации компонентов в правой части уравнения через соответствующие константы, ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-638.png)
Решая последнее уравнение относительно ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-640.png)
Формула (3.7) упрощается при пренебрежении малыми величинами и при допущении
Например, если ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-643.png)
Для приближенных расчетов разных случаев кислотно-основного равновесия можно воспользоваться формулами таблицы 3.1. Значения ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-645.png)
В случаях, когда нельзя считать равновесную концентрацию ионизирующегося вещества равной его аналитической концентрации (не соблюдается условие ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-646.png)
Пример 3.1.
Рассчитайте ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-647.png)
0,10 М раствора ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-648.png)
Решение:
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-648.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-649.png)
Проверка условия ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-651.png)
Таблица 3.1
Формулы для приближенного расчета ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-653.png)
Пример 3.2.
Рассчитайте ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-655.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-656.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-657.png)
Решение:
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-657.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-658.png)
Поскольку ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-660.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-661.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-661.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-661.png)
откуда:
Решаем квадратное уравнение относительно ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-661.png)
Пример 3.3.
Рассчитайте pH 0,010 М раствора муравьиной кислоты в присутствии 0,010 М ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-665.png)
Решение:
Отношение ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-666.png)
С учетом соотношения (2.11) термодинамической и реальной констант:
Пример 3.4.
Рассчитайте ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-822.png)
Решение:
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-824.png)
Запишем уравнение электронейтральности:
Тогда:
откуда: ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-836.png)
Без учета автопротолиза воды:
pH = 7, расчет менее точен.
Подобный подход необходим и при расчете pH очень разбавленных ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-840.png)
Пример 3.5.
Рассчитайте ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-842.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-843.png)
Решение:
Определяем тип гидролизующейся соли (тип протолита).
Гидролиз протекает по аниону, т. е. ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-845.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-846.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-847.png)
Поскольку ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-851.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-853.png)
отсюда:
Решаем квадратное уравнение:
Находим степень гидролиза ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-858.png)
Пример 3.6.
К 50 мл 0,10 М раствора ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-860.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-861.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-863.png)
Решение:
После смешивания двух растворов получаем:
В результате взаимодействия протолитов в растворе образуется кислая соль (амфолит) согласно уравнению реакции:
Для угольной кислоты ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-866.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-868.png)
Пример 3.7.*
К 20 мл 0,20 М раствора соли аммония в безводном метаноле добавили 10 мл 0,20 М раствора метилата натрия в безводном метаноле. Определите: а) pH исходного раствора соли; в) pH полученного раствора, если для метанола ![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-871.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-873.png)
Решение:
а) в метанольном растворе протекает протолитическая реакция:
Откуда
б) протолитическая реакция взаимодействия при сливании двух растворов:
Значение константы равновесия реакции:
указывает на ее практическую необратимость и возможность приближенных расчетов. Используя эту константу или формулу для расчета pH в растворе, содержащем кислотно-основную сопряженную пару (3.11), можно вычислить pH полученного раствора:
откуда
Эти примеры взяты со страницы примеров решения задач по аналитической химии:
Решение задач по аналитической химии
Возможны вам будут полезны эти страницы:

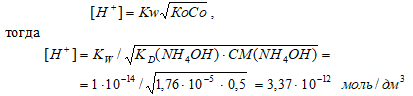


![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-584.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-588.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-589.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-590.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-591.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-596.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-597.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-599.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-600.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-601.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-603.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-604.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-605.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-606.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-607.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-609.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-610.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-618.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-619.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-621.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-623.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-624.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-627.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-630.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-633.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-634.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-637.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-639.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-641.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-642.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-644.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-650.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-652.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-654.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-659.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-662.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-663.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-664.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-667.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-668.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-821.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-825.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-833.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-835.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-838.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-839.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-844.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-848.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-850.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-855.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-856.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-857.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-859.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-864.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-865.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-870.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-875.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-877.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-878.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-879.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-881.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-882.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-884.png)
![Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения](https://lfirmal.com/wp-content/uploads/2020/03/%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-885.png)
