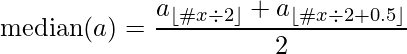Как найти медиану числа питон

To calculate the median value in Python:

Import the statistics module.
Call the statistics.median() function on a list of numbers.

For example, let’s calculate the median of a list of numbers:

import statistics

numbers = [1, 2, 3, 4, 5, 6, 7]
med = statistics.median(numbers)

print(med)

Output:

The median value is a common way to measure the “centrality” of a dataset.

If you are looking for a quick answer, I’m sure the above example will do. But to really learn what median really is, why it is useful, and how to find it, read along.

This is a comprehensive guide to finding the median in Python.

What Is the Median Value in Maths

The Median is the middle value of a given dataset.

If you have a list of 3 numbers, the median is the second number as it is in the middle.

But in case you have a list of 4 values, there is no “middle value”. When calculating the median, of an even-sized dataset, the average of the two middle values is used.

Why and When Is Median Value Useful

When dealing with statistics, you usually want to have a single number that describes the nature of a dataset.

Think about your school grades for example. Instead of seeing the dozens of grades, you want to know the average (the mean).

Usually, measuring the “centrality” of a dataset means calculating the mean value. But if you have a skewed distribution, the mean value can be unintuitive.

Let’s say you drive to your nearby shopping mall 7 times. Usually, the drive takes around 10 minutes. But one day the traffic jam makes it last 2 hours.

Here is a list of driving times to the mall:

[9, 120, 10, 9, 10, 10, 10]

Now if you take the average of this list, you get ~25 minutes. But how well does this number really describe your trip?

Pretty badly.

As you can see, most of the time the trip takes around 10 minutes.

To better describe the driving time, you should use a median value instead. To calculate the median value, you need to sort the driving times first:

[9, 9, 10, 10, 10, 10, 120]

Then you can choose the middle value, which in this case is 10 minutes. 10 minutes describes your typical trip length way better than 25, right?

The usefulness of calculating the median, in this case, is that the unusually high value of 120 does not matter.

In short, you can calculate the median value when measuring centrality with average is unintuitive.

In Python, you can either create a function that calculates the median or use existing functionality.

How to Implement Median Function in Python

If you want to implement the median function, you need to understand the procedure of finding the median.

The median function works such that it:

Takes a dataset as input.
Sorts the dataset.
Checks if the dataset is odd/even in length.
If the dataset is odd in length, the function picks the mid-value and returns it.
If the dataset is even, the function picks the two mid values, calculates the average, and returns the result.

Here is how it looks in the code:

def median(data):
    sorted_data = sorted(data)
    data_len = len(sorted_data)

    middle = (data_len - 1) // 2

    if middle % 2:
        return sorted_data[middle]
    else:
        return (sorted_data[middle] + sorted_data[middle + 1]) / 2.0

Example usage:

numbers = [1, 2, 3, 4, 5, 6, 7]
med = median(numbers)

print(med)

Output:

Now, this is a valid approach if you need to write the median function yourself. But with common maths operations, you should use a built-in function to save time and headaches.

Let’s next take a look at how to calculate the median with a built-in function in Python.

How to Use a Built-In Median Function in Python

In Python, there is a module called statistics. This module contains useful mathematical tools for data science and statistics.

One of the great methods of this module is the median() function.

As the name suggests, this function calculates the median of a given dataset.

To use the median function from the statistics module, remember to import it into your project.

Here is an example of calculating the median for a bunch of numbers:

import statistics

numbers = [1, 2, 3, 4, 5, 6, 7]
med = statistics.median(numbers)

print(med)

Result:

Conclusion

Today you learned how to calculate the median value in Python.

To recap, the median value is a way to measure the centrality of a dataset. The Median is useful when the average doesn’t properly describe the dataset and gives falsy results.

To calculate the median in Python, use the built-in median() function from the statistics module.

import statistics

numbers = [1, 2, 3, 4, 5, 6, 7]
med = statistics.median(numbers)

Thanks for reading. Happy coding!

What is median?

Median is a descriptive statistic that is used as a measure of central tendency of a distribution. It is equal to the middle value of the distribution. There are equal number of values smaller and larger than the median. It is also not much sensitive to the presence of outliers in the data like the mean (another measure of central tendency).

To calculate the median of a list of values –

Sort the values in ascending or descending order (either works).
If the number of values, n, is odd, then the median is the value in the (n+1)/2 position in the sorted list(or array) of values.
If the number of values, n, is even, then the median is the average of the values in n/2 and n/2 + 1 position in the sorted list(or array) of values.

For example, calculate the median of the following values –

First, let’s sort these numbers in ascending order.

Now, since the total number of values is even (8), the median is the average of the 4th and the 5th value.

Thus, median comes out to be 3.5

Now that we have seen how is the median mathematically calculated, let’s look at how to compute the median in Python.

To compute the median of a list of values in Python, you can write your own function, or use methods available in libraries like numpy, statistics, etc. Let’s look at these methods with the help of examples.

1. From scratch implementation of median in Python

You can write your own function in Python to compute the median of a list.

def get_median(ls):
    # sort the list
    ls_sorted = ls.sort()
    # find the median
    if len(ls) % 2 != 0:
        # total number of values are odd
        # subtract 1 since indexing starts at 0
        m = int((len(ls)+1)/2 - 1)
        return ls[m]
    else:
        m1 = int(len(ls)/2 - 1)
        m2 = int(len(ls)/2)
        return (ls[m1]+ls[m2])/2

# create a list
ls = [3, 1, 4, 9, 2, 5, 3, 6]
# get the median
print(get_median(ls))

Output:

3.5

Here, we use the list sort() function to sort the list, and then depending upon the length of the list return the median. We get 3.5 as the median, the same we manually calculated above.

Note that, compared to the above function, the libraries you’ll see next are better optimized to compute the median of a list of values.

2. Using `statistics` library

You can also use the statistics standard library in Python to get the median of a list. Pass the list as argument to the statistics.median() function.

import statistics

# create a list
ls = [3, 1, 4, 9, 2, 5, 3, 6]
# get the median
print(statistics.median(ls))

Output:

3.5

We get the same results as above.

For more on the statistics library in Python, refer to its documentation.

3. Using `numpy` library

The numpy library’s median() function is generally used to calculate the median of a numpy array. You can also use this function on a Python list.

import numpy as np

# create a list
ls = [3, 1, 4, 9, 2, 5, 3, 6]
print(np.median(ls))

Output:

3.5

You can see that we get the same result.

Subscribe to our newsletter for more informative guides and tutorials.
We do not spam and you can opt out any time.

Piyush is a data professional passionate about using data to understand things better and make informed decisions. He has experience working as a Data Scientist in the consulting domain and holds an engineering degree from IIT Roorkee. His hobbies include watching cricket, reading, and working on side projects.

View all posts

Источник

How do you find the median of a list in Python? The list can be of any size and the numbers are not guaranteed to be in any particular order.

If the list contains an even number of elements, the function should return the average of the middle two.

Here are some examples (sorted for display purposes):

median([1]) == 1
median([1, 1]) == 1
median([1, 1, 2, 4]) == 1.5
median([0, 2, 5, 6, 8, 9, 9]) == 6
median([0, 0, 0, 0, 4, 4, 6, 8]) == 2

Veedrac

57.6k14 gold badges111 silver badges168 bronze badges

asked Jun 7, 2014 at 21:04

Python 3.4 has statistics.median:

Return the median (middle value) of numeric data.

When the number of data points is odd, return the middle data point.
When the number of data points is even, the median is interpolated by taking the average of the two middle values:
>>> median([1, 3, 5])
3
>>> median([1, 3, 5, 7])
4.0

Usage:

import statistics

items = [6, 1, 8, 2, 3]

statistics.median(items)
#>>> 3

It’s pretty careful with types, too:

statistics.median(map(float, items))
#>>> 3.0

from decimal import Decimal
statistics.median(map(Decimal, items))
#>>> Decimal('3')

answered Jun 8, 2014 at 0:08

VeedracVeedrac

57.6k14 gold badges111 silver badges168 bronze badges

(Works with python-2.x):

def median(lst):
    n = len(lst)
    s = sorted(lst)
    return (s[n//2-1]/2.0+s[n//2]/2.0, s[n//2])[n % 2] if n else None

>>> median([-5, -5, -3, -4, 0, -1])
-3.5

numpy.median():

>>> from numpy import median
>>> median([1, -4, -1, -1, 1, -3])
-1.0

For python-3.x, use statistics.median:

>>> from statistics import median
>>> median([5, 2, 3, 8, 9, -2])
4.0

answered Jun 7, 2014 at 23:33

A.J. UppalA.J. Uppal

19k6 gold badges45 silver badges76 bronze badges

The sorted() function is very helpful for this. Use the sorted function
to order the list, then simply return the middle value (or average the two middle
values if the list contains an even amount of elements).

def median(lst):
    sortedLst = sorted(lst)
    lstLen = len(lst)
    index = (lstLen - 1) // 2
   
    if (lstLen % 2):
        return sortedLst[index]
    else:
        return (sortedLst[index] + sortedLst[index + 1])/2.0

vvvvv

23.8k19 gold badges48 silver badges75 bronze badges

answered Jun 7, 2014 at 22:09

swolfeswolfe

9065 silver badges8 bronze badges

Of course in Python3 you can use built in functions, but if you are using Python2 or just would like to create your own you can do something like this. The trick here is to use ~ operator that flip positive number to negative. For instance ~2 -> -3 and using negative in for list in Python will count items from the end. So if you have mid == 2 then it will take third element from beginning and third item from the end.

def median(data):
    data.sort()
    mid = len(data) // 2
    return (data[mid] + data[~mid]) / 2.0

answered Jan 21, 2018 at 17:22

Vlad BezdenVlad Bezden

82.1k24 gold badges246 silver badges179 bronze badges

Here’s a cleaner solution:

def median(lst):
    quotient, remainder = divmod(len(lst), 2)
    if remainder:
        return sorted(lst)[quotient]
    return sum(sorted(lst)[quotient - 1:quotient + 1]) / 2.

Note: Answer changed to incorporate suggestion in comments.

SiHa

7,62313 gold badges32 silver badges41 bronze badges

answered Apr 25, 2015 at 20:18

You can try the quickselect algorithm if faster average-case running times are needed. Quickselect has average (and best) case performance O(n), although it can end up O(n²) on a bad day.

Here’s an implementation with a randomly chosen pivot:

import random

def select_nth(n, items):
    pivot = random.choice(items)

    lesser = [item for item in items if item < pivot]
    if len(lesser) > n:
        return select_nth(n, lesser)
    n -= len(lesser)

    numequal = items.count(pivot)
    if numequal > n:
        return pivot
    n -= numequal

    greater = [item for item in items if item > pivot]
    return select_nth(n, greater)

You can trivially turn this into a method to find medians:

def median(items):
    if len(items) % 2:
        return select_nth(len(items)//2, items)

    else:
        left  = select_nth((len(items)-1) // 2, items)
        right = select_nth((len(items)+1) // 2, items)

        return (left + right) / 2

This is very unoptimised, but it’s not likely that even an optimised version will outperform Tim Sort (CPython’s built-in sort) because that’s really fast. I’ve tried before and I lost.

answered Jun 8, 2014 at 0:49

VeedracVeedrac

57.6k14 gold badges111 silver badges168 bronze badges

You can use the list.sort to avoid creating new lists with sorted and sort the lists in place.

Also you should not use list as a variable name as it shadows python’s own list.

def median(l):
    half = len(l) // 2
    l.sort()
    if not len(l) % 2:
        return (l[half - 1] + l[half]) / 2.0
    return l[half]

answered Jun 7, 2014 at 22:48

def median(x):
    x = sorted(x)
    listlength = len(x) 
    num = listlength//2
    if listlength%2==0:
        middlenum = (x[num]+x[num-1])/2
    else:
        middlenum = x[num]
    return middlenum

Sam Mason

14.8k1 gold badge41 silver badges59 bronze badges

answered Sep 25, 2018 at 18:22

BulentBulent

911 silver badge1 bronze badge

def median(array):
    """Calculate median of the given list.
    """
    # TODO: use statistics.median in Python 3
    array = sorted(array)
    half, odd = divmod(len(array), 2)
    if odd:
        return array[half]
    return (array[half - 1] + array[half]) / 2.0

answered Mar 4, 2016 at 11:50

warvariucwarvariuc

56.6k40 gold badges173 silver badges227 bronze badges

A simple function to return the median of the given list:

def median(lst):
    lst = sorted(lst)  # Sort the list first
    if len(lst) % 2 == 0:  # Checking if the length is even
        # Applying formula which is sum of middle two divided by 2
        return (lst[len(lst) // 2] + lst[(len(lst) - 1) // 2]) / 2
    else:
        # If length is odd then get middle value
        return lst[len(lst) // 2]

Some examples with the median function:

>>> median([9, 12, 20, 21, 34, 80])  # Even
20.5
>>> median([9, 12, 80, 21, 34])  # Odd
21

If you want to use library you can just simply do:

>>> import statistics
>>> statistics.median([9, 12, 20, 21, 34, 80])  # Even
20.5
>>> statistics.median([9, 12, 80, 21, 34])  # Odd
21

Asclepius

56.4k17 gold badges164 silver badges142 bronze badges

answered Jul 5, 2020 at 23:16

The AGThe AG

6529 silver badges18 bronze badges

I posted my solution at Python implementation of «median of medians» algorithm , which is a little bit faster than using sort(). My solution uses 15 numbers per column, for a speed ~5N which is faster than the speed ~10N of using 5 numbers per column. The optimal speed is ~4N, but I could be wrong about it.

Per Tom’s request in his comment, I added my code here, for reference. I believe the critical part for speed is using 15 numbers per column, instead of 5.

#!/bin/pypy
#
# TH @stackoverflow, 2016-01-20, linear time "median of medians" algorithm
#
import sys, random


items_per_column = 15


def find_i_th_smallest( A, i ):
    t = len(A)
    if(t <= items_per_column):
        # if A is a small list with less than items_per_column items, then:
        #
        # 1. do sort on A
        # 2. find i-th smallest item of A
        #
        return sorted(A)[i]
    else:
        # 1. partition A into columns of k items each. k is odd, say 5.
        # 2. find the median of every column
        # 3. put all medians in a new list, say, B
        #
        B = [ find_i_th_smallest(k, (len(k) - 1)/2) for k in [A[j:(j + items_per_column)] for j in range(0,len(A),items_per_column)]]

        # 4. find M, the median of B
        #
        M = find_i_th_smallest(B, (len(B) - 1)/2)


        # 5. split A into 3 parts by M, { < M }, { == M }, and { > M }
        # 6. find which above set has A's i-th smallest, recursively.
        #
        P1 = [ j for j in A if j < M ]
        if(i < len(P1)):
            return find_i_th_smallest( P1, i)
        P3 = [ j for j in A if j > M ]
        L3 = len(P3)
        if(i < (t - L3)):
            return M
        return find_i_th_smallest( P3, i - (t - L3))


# How many numbers should be randomly generated for testing?
#
number_of_numbers = int(sys.argv[1])


# create a list of random positive integers
#
L = [ random.randint(0, number_of_numbers) for i in range(0, number_of_numbers) ]


# Show the original list
#
# print L


# This is for validation
#
# print sorted(L)[int((len(L) - 1)/2)]


# This is the result of the "median of medians" function.
# Its result should be the same as the above.
#
print find_i_th_smallest( L, (len(L) - 1) / 2)

answered Jan 21, 2016 at 0:00

In case you need additional information on the distribution of your list, the percentile method will probably be useful. And a median value corresponds to the 50th percentile of a list:

import numpy as np
a = np.array([1,2,3,4,5,6,7,8,9])
median_value = np.percentile(a, 50) # return 50th percentile
print median_value

answered Apr 22, 2020 at 12:07

Gabriel123Gabriel123

4165 silver badges11 bronze badges

Here what I came up with during this exercise in Codecademy:

def median(data):
    new_list = sorted(data)
    if len(new_list)%2 > 0:
        return new_list[len(new_list)/2]
    elif len(new_list)%2 == 0:
        return (new_list[(len(new_list)/2)] + new_list[(len(new_list)/2)-1]) /2.0

print median([1,2,3,4,5,9])

answered May 27, 2016 at 8:52

Just two lines are enough.

def get_median(arr):
    '''
    Calculate the median of a sequence.
    :param arr: list
    :return: int or float
    '''
    arr = sorted(arr)
    return arr[len(arr)//2] if len(arr) % 2 else (arr[len(arr)//2] + arr[len(arr)//2-1])/2

Asclepius

56.4k17 gold badges164 silver badges142 bronze badges

answered Sep 17, 2020 at 2:32

Rt.TongRt.Tong

1863 silver badges5 bronze badges

median Function

def median(midlist):
    midlist.sort()
    lens = len(midlist)
    if lens % 2 != 0: 
        midl = (lens / 2)
        res = midlist[midl]
    else:
        odd = (lens / 2) -1
        ev = (lens / 2) 
        res = float(midlist[odd] + midlist[ev]) / float(2)
    return res

answered May 21, 2015 at 13:55

I had some problems with lists of float values. I ended up using a code snippet from the python3 statistics.median and is working perfect with float values without imports. source

def calculateMedian(list):
    data = sorted(list)
    n = len(data)
    if n == 0:
        return None
    if n % 2 == 1:
        return data[n // 2]
    else:
        i = n // 2
        return (data[i - 1] + data[i]) / 2

answered May 3, 2017 at 16:54

DanDan

7471 gold badge7 silver badges20 bronze badges

def midme(list1):

    list1.sort()
    if len(list1)%2>0:
            x = list1[int((len(list1)/2))]
    else:
            x = ((list1[int((len(list1)/2))-1])+(list1[int(((len(list1)/2)))]))/2
    return x


midme([4,5,1,7,2])

answered Feb 18, 2018 at 18:00

vk123vk123

213 bronze badges

def median(array):
    if len(array) < 1:
        return(None)
    if len(array) % 2 == 0:
        median = (array[len(array)//2-1: len(array)//2+1])
        return sum(median) / len(median)
    else:
        return(array[len(array)//2])

answered Apr 6, 2018 at 21:55

I defined a median function for a list of numbers as

def median(numbers):
    return (sorted(numbers)[int(round((len(numbers) - 1) / 2.0))] + sorted(numbers)[int(round((len(numbers) - 1) // 2.0))]) / 2.0

answered Oct 14, 2014 at 14:12

import numpy as np
def get_median(xs):
        mid = len(xs) // 2  # Take the mid of the list
        if len(xs) % 2 == 1: # check if the len of list is odd
            return sorted(xs)[mid] #if true then mid will be median after sorting
        else:
            #return 0.5 * sum(sorted(xs)[mid - 1:mid + 1])
            return 0.5 * np.sum(sorted(xs)[mid - 1:mid + 1]) #if false take the avg of mid
print(get_median([7, 7, 3, 1, 4, 5]))
print(get_median([1,2,3, 4,5]))

answered Aug 26, 2019 at 7:12

A more generalized approach for median (and percentiles) would be:

def get_percentile(data, percentile):
    # Get the number of observations
    cnt=len(data)
    # Sort the list
    data=sorted(data)
    # Determine the split point
    i=(cnt-1)*percentile
    # Find the `floor` of the split point
    diff=i-int(i)
    # Return the weighted average of the value above and below the split point
    return data[int(i)]*(1-diff)+data[int(i)+1]*(diff)

# Data
data=[1,2,3,4,5]
# For the median
print(get_percentile(data=data, percentile=.50))
# > 3
print(get_percentile(data=data, percentile=.75))
# > 4

# Note the weighted average difference when an int is not returned by the percentile
print(get_percentile(data=data, percentile=.51))
# > 3.04

answered May 7, 2020 at 19:46

conmakconmak

1,15010 silver badges13 bronze badges

Try This

import math
def find_median(arr):
    if len(arr)%2==1:
        med=math.ceil(len(arr)/2)-1
        return arr[med]
    else:
        return -1
print(find_median([1,2,3,4,5,6,7,8]))

answered Dec 20, 2021 at 13:32

0xN1nja0xN1nja

8281 gold badge9 silver badges17 bronze badges

Implement it:

def median(numbers):
    """
    Calculate median of a list numbers.
    :param numbers: the numbers to be calculated.
    :return: median value of numbers.

    >>> median([1, 3, 3, 6, 7, 8, 9])
    6
    >>> median([1, 2, 3, 4, 5, 6, 8, 9])
    4.5
    >>> import statistics
    >>> import random
    >>> numbers = random.sample(range(-50, 50), k=100)
    >>> statistics.median(numbers) == median(numbers)
    True
    """
    numbers = sorted(numbers)
    mid_index = len(numbers) // 2
    return (
        (numbers[mid_index] + numbers[mid_index - 1]) / 2 if mid_index % 2 == 0
        else numbers[mid_index]
    )


if __name__ == "__main__":
    from doctest import testmod

    testmod()

source from

Asclepius

56.4k17 gold badges164 silver badges142 bronze badges

answered Oct 4, 2020 at 16:36

duyuanchaoduyuanchao

3,7631 gold badge25 silver badges16 bronze badges

Function median:

def median(d):
    d=np.sort(d)
    n2=int(len(d)/2)
    r=n2%2
    if (r==0):
        med=d[n2] 
    else:
        med=(d[n2] + d[n2+1]) / 2
    return med

answered Feb 15, 2020 at 11:03

Simply, Create a Median Function with an argument as a list of the number and call the function.

def median(l):
    l = sorted(l)
    lent = len(l)
    if (lent % 2) == 0:
        m = int(lent / 2)
        result = l[m]
    else:
        m = int(float(lent / 2) - 0.5)
        result = l[m]
    return result

Asclepius

56.4k17 gold badges164 silver badges142 bronze badges

answered Apr 27, 2021 at 5:17

What I did was this:

def median(a):
    a = sorted(a)
    if len(a) / 2 != int:
        return a[len(a) / 2]
    else:
        return (a[len(a) / 2] + a[(len(a) / 2) - 1]) / 2

Explanation: Basically if the number of items in the list is odd, return the middle number, otherwise, if you half an even list, python automatically rounds the higher number so we know the number before that will be one less (since we sorted it) and we can add the default higher number and the number lower than it and divide them by 2 to find the median.

Asclepius

56.4k17 gold badges164 silver badges142 bronze badges

answered Nov 6, 2020 at 6:31

Here’s the tedious way to find median without using the median function:

def median(*arg):
    order(arg)
    numArg = len(arg)
    half = int(numArg/2)
    if numArg/2 ==half:
        print((arg[half-1]+arg[half])/2)
    else:
        print(int(arg[half]))

def order(tup):
    ordered = [tup[i] for i in range(len(tup))]
    test(ordered)
    while(test(ordered)):
        test(ordered)
    print(ordered)


def test(ordered):
    whileloop = 0 
    for i in range(len(ordered)-1):
        print(i)
        if (ordered[i]>ordered[i+1]):
            print(str(ordered[i]) + ' is greater than ' + str(ordered[i+1]))
            original = ordered[i+1]
            ordered[i+1]=ordered[i]
            ordered[i]=original
            whileloop = 1 #run the loop again if you had to switch values
    return whileloop

answered Jan 24, 2017 at 19:05

I LikeI Like

1,6812 gold badges25 silver badges50 bronze badges

It is very simple;

def median(alist):
    #to find median you will have to sort the list first
    sList = sorted(alist)
    first = 0
    last = len(sList)-1
    midpoint = (first + last)//2
    return midpoint

And you can use the return value like this median = median(anyList)

answered Dec 7, 2018 at 16:11

FarhanFarhan

1,44315 silver badges23 bronze badges

Источник

New in version 3.4.

Source code: Lib/statistics.py

This module provides functions for calculating mathematical statistics of
numeric (Real-valued) data.

Note

Unless explicitly noted otherwise, these functions support int,
float, decimal.Decimal and fractions.Fraction.
Behaviour with other types (whether in the numeric tower or not) is
currently unsupported. Mixed types are also undefined and
implementation-dependent. If your input data consists of mixed types,
you may be able to use map() to ensure a consistent result, e.g.
map(float, input_data).

9.7.1. Averages and measures of central location¶

These functions calculate an average or typical value from a population
or sample.

`mean()`	Arithmetic mean (“average”) of data.
`harmonic_mean()`	Harmonic mean of data.
`median()`	Median (middle value) of data.
`median_low()`	Low median of data.
`median_high()`	High median of data.
`median_grouped()`	Median, or 50th percentile, of grouped data.
`mode()`	Mode (most common value) of discrete data.

9.7.2. Measures of spread¶

These functions calculate a measure of how much the population or sample
tends to deviate from the typical or average values.

`pstdev()`	Population standard deviation of data.
`pvariance()`	Population variance of data.
`stdev()`	Sample standard deviation of data.
`variance()`	Sample variance of data.

9.7.3. Function details¶

Note: The functions do not require the data given to them to be sorted.
However, for reading convenience, most of the examples show sorted sequences.

statistics.mean(data)¶

Return the sample arithmetic mean of data which can be a sequence or iterator.

The arithmetic mean is the sum of the data divided by the number of data
points. It is commonly called “the average”, although it is only one of many
different mathematical averages. It is a measure of the central location of
the data.

If data is empty, StatisticsError will be raised.

Some examples of use:

>>> mean([1, 2, 3, 4, 4])
2.8
>>> mean([-1.0, 2.5, 3.25, 5.75])
2.625

>>> from fractions import Fraction as F
>>> mean([F(3, 7), F(1, 21), F(5, 3), F(1, 3)])
Fraction(13, 21)

>>> from decimal import Decimal as D
>>> mean([D("0.5"), D("0.75"), D("0.625"), D("0.375")])
Decimal('0.5625')

Note

The mean is strongly affected by outliers and is not a robust estimator
for central location: the mean is not necessarily a typical example of the
data points. For more robust, although less efficient, measures of
central location, see median() and mode(). (In this case,
“efficient” refers to statistical efficiency rather than computational
efficiency.)

The sample mean gives an unbiased estimate of the true population mean,
which means that, taken on average over all the possible samples,
mean(sample) converges on the true mean of the entire population. If
data represents the entire population rather than a sample, then
mean(data) is equivalent to calculating the true population mean μ.

statistics.harmonic_mean(data)¶

Return the harmonic mean of data, a sequence or iterator of
real-valued numbers.

The harmonic mean, sometimes called the subcontrary mean, is the
reciprocal of the arithmetic mean() of the reciprocals of the
data. For example, the harmonic mean of three values a, b and c
will be equivalent to 3/(1/a + 1/b + 1/c).

The harmonic mean is a type of average, a measure of the central
location of the data. It is often appropriate when averaging quantities
which are rates or ratios, for example speeds. For example:

Suppose an investor purchases an equal value of shares in each of
three companies, with P/E (price/earning) ratios of 2.5, 3 and 10.
What is the average P/E ratio for the investor’s portfolio?

>>> harmonic_mean([2.5, 3, 10])  # For an equal investment portfolio.
3.6

Using the arithmetic mean would give an average of about 5.167, which
is too high.

StatisticsError is raised if data is empty, or any element
is less than zero.

New in version 3.6.

statistics.median(data)¶

Return the median (middle value) of numeric data, using the common “mean of
middle two” method. If data is empty, StatisticsError is raised.
data can be a sequence or iterator.

The median is a robust measure of central location, and is less affected by
the presence of outliers in your data. When the number of data points is
odd, the middle data point is returned:

When the number of data points is even, the median is interpolated by taking
the average of the two middle values:

>>> median([1, 3, 5, 7])
4.0

This is suited for when your data is discrete, and you don’t mind that the
median may not be an actual data point.

statistics.median_low(data)¶

Return the low median of numeric data. If data is empty,
StatisticsError is raised. data can be a sequence or iterator.

The low median is always a member of the data set. When the number of data
points is odd, the middle value is returned. When it is even, the smaller of
the two middle values is returned.

>>> median_low([1, 3, 5])
3
>>> median_low([1, 3, 5, 7])
3

Use the low median when your data are discrete and you prefer the median to
be an actual data point rather than interpolated.

statistics.median_high(data)¶

Return the high median of data. If data is empty, StatisticsError
is raised. data can be a sequence or iterator.

The high median is always a member of the data set. When the number of data
points is odd, the middle value is returned. When it is even, the larger of
the two middle values is returned.

>>> median_high([1, 3, 5])
3
>>> median_high([1, 3, 5, 7])
5

Use the high median when your data are discrete and you prefer the median to
be an actual data point rather than interpolated.

statistics.median_grouped(data, interval=1)¶

Return the median of grouped continuous data, calculated as the 50th
percentile, using interpolation. If data is empty, StatisticsError
is raised. data can be a sequence or iterator.

>>> median_grouped([52, 52, 53, 54])
52.5

In the following example, the data are rounded, so that each value represents
the midpoint of data classes, e.g. 1 is the midpoint of the class 0.5–1.5, 2
is the midpoint of 1.5–2.5, 3 is the midpoint of 2.5–3.5, etc. With the data
given, the middle value falls somewhere in the class 3.5–4.5, and
interpolation is used to estimate it:

>>> median_grouped([1, 2, 2, 3, 4, 4, 4, 4, 4, 5])
3.7

Optional argument interval represents the class interval, and defaults
to 1. Changing the class interval naturally will change the interpolation:

>>> median_grouped([1, 3, 3, 5, 7], interval=1)
3.25
>>> median_grouped([1, 3, 3, 5, 7], interval=2)
3.5

This function does not check whether the data points are at least
interval apart.

CPython implementation detail: Under some circumstances, median_grouped() may coerce data points to
floats. This behaviour is likely to change in the future.

9.7.4. Exceptions¶

A single exception is defined:

exception statistics.StatisticsError¶: Subclass of ValueError for statistics-related exceptions.

Источник

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

Python is a very popular language when it comes to data analysis and statistics. Luckily, Python3 provide statistics module, which comes with very useful functions like mean(), median(), mode() etc.
median() function in the statistics module can be used to calculate median value from an unsorted data-list. The biggest advantage of using median() function is that the data-list does not need to be sorted before being sent as parameter to the median() function.
Median is the value that separates the higher half of a data sample or probability distribution from the lower half. For a dataset, it may be thought of as the middle value. The median is the measure of the central tendency of the properties of a data-set in statistics and probability theory. Median has a very big advantage over Mean, which is the median value is not skewed so much by extremely large or small values. The median value is either contained in the data-set of values provided or it doesn’t sway too much from the data provided.
For odd set of elements, the median value is the middle one.
For even set of elements, the median value is the mean of two middle elements.

Median can be represented by the following formula :

Syntax : median( [data-set] )
Parameters :
[data-set] : List or tuple or an iterable with a set of numeric values
Returns : Return the median (middle value) of the iterable containing the data
Exceptions : StatisticsError is raised when iterable passed is empty or when list is null.

Code #1 : Working

Python3

import statistics

data1 = [2, -2, 3, 6, 9, 4, 5, -1]

print("Median of data-set is : % s "

% (statistics.median(data1)))

Output :

Median of data-set is : 3.5

Code #2 :

Python3

from statistics import median

from fractions import Fraction as fr

data1 = (2, 3, 4, 5, 7, 9, 11)

data2 = (2.4, 5.1, 6.7, 8.9)

data3 = (fr(1, 2), fr(44, 12),

fr(10, 3), fr(2, 3))

data4 = (-5, -1, -12, -19, -3)

data5 = (-1, -2, -3, -4, 4, 3, 2, 1)

print("Median of data-set 1 is % s" % (median(data1)))

print("Median of data-set 2 is % s" % (median(data2)))

print("Median of data-set 3 is % s" % (median(data3)))

print("Median of data-set 4 is % s" % (median(data4)))

print("Median of data-set 5 is % s" % (median(data5)))

Output :

Median of data-set 1 is 5
Median of data-set 2 is 5.9
Median of data-set 3 is 2
Median of data-set 4 is -5
Median of data-set 5 is 0.0

Code #3 : Demonstrating StatisticsError

Python3

from statistics import median

empty = []

print(median(empty))

Output :

Traceback (most recent call last):
  File "/home/3c98774036f97845ee9f65f6d3571e49.py", line 12, in 
    print(median(empty))
  File "/usr/lib/python3.5/statistics.py", line 353, in median
    raise StatisticsError("no median for empty data")
statistics.StatisticsError: no median for empty data

Applications :
For practical applications, different measures of dispersion and population tendency are compared on the basis of how well the corresponding population values can be estimated. For example, a comparison shows that the sample mean is more statistically efficient than the sample median when the data is uncontaminated by data from heavily-tailed data distribution or from mixtures of data distribution, but less efficient otherwise and that the efficiency of the sample median is higher than that for a wide range of distributions. To be more specific, the median has 64% efficiency compared to minimum-variance-mean ( for large normal samples ).

Last Updated :
27 Sep, 2021

Like Article

Save Article

Источник

What Is the Median Value in Maths

Why and When Is Median Value Useful

How to Implement Median Function in Python

How to Use a Built-In Median Function in Python

Conclusion

Further Reading

About the Author

Recent Posts

What is median?

1. From scratch implementation of median in Python

2. Using `statistics` library

3. Using `numpy` library

9.7.1. Averages and measures of central location¶

9.7.2. Measures of spread¶

9.7.3. Function details¶

9.7.4. Exceptions¶

Python3

Python3

Python3

Не пропустите также:

What Is the Median Value in Maths

Why and When Is Median Value Useful

How to Implement Median Function in Python

How to Use a Built-In Median Function in Python

Conclusion

Further Reading

About the Author

Recent Posts

What is median?

1. From scratch implementation of median in Python

2. Using statistics library

3. Using numpy library

9.7.1. Averages and measures of central location¶

9.7.2. Measures of spread¶

9.7.3. Function details¶

9.7.4. Exceptions¶

Python3

Python3

Python3

Не пропустите также:

2. Using `statistics` library

3. Using `numpy` library