Теоремы о свойствах алгебраических многочленов
Пусть 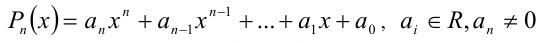
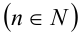
Теорема 1 (о разложении многочлена произвольной степени на произведение линейных и квадратичных множителей). Многочлен 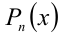
Теорема 2. Многочлен нечётной степени имеет хотя бы один действительный корень.
Теорема 3 (основная теорема алгебры). Многочлен n -й степени имеет ровно n корней (действительных и комплексных), в том числе действительных не больше n (сучётом их кратности).
Теорема 4. Если на концах некоторого отрезка [a, b ] значения многочлена имеют разные знаки, то на интервале (а, b) существует хотя бы один корень этого многочлена.
Заметим, что аналогичное утверждение справедливо не только для многочленов, но и для любой непрерывной на отрезке [ a,b ] функции.
Теорема 5 (условие тождественного равенства двух многочленов). Два алгебраических многочлена
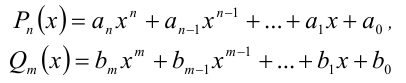
тождественно равны (т.е. равны при всех 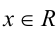
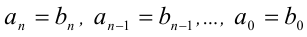
Пример №169.
Определить три числа p, q и r такие, что равенство 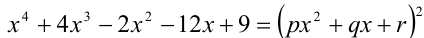
Решение:
Раскроем (вспомним соответствующую формулу сокращённого умножения) квадрат в правой части и приведём полученный многочлен к стандартному виду:
Многочлены, стоящие слева и справа от знака равенства, тождественно равны тогда и только тогда, когда выполняется система
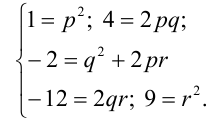
Ответ:
Теорема 6. Если значения двух многочленов степени не выше n совпадают в n + 1 различных точках, то эти многочлены тождественно равны.
Например, если две параболы (графики квадратичных функций 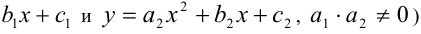
Теорема 7 (формула деления многочлена на многочлен с остатком). Для любых двух алгебраических многочленов
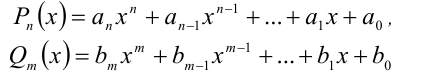
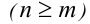
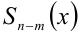
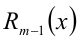
Здесь 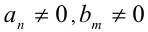

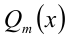
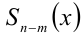

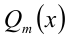
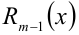
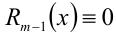

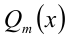
Пример №170.
Найти остаток от деления многочлена 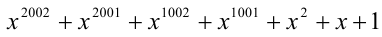
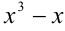
Решение:
В данной задаче весьма проблематично было бы искать многочлен-остаток непосредственным делением многочлена на многочлен из-за слишком высокой степени многочлена-делимого. Запишем результат деления первого многочлена на второй в виде формулы
Здесь 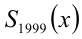
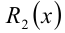
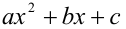
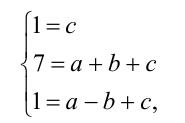
решая которую найдём искомые коэффициенты а = b = 3 , c = 1 . Поэтому остаток от деления равен
Следующая теорема названа по имени французского математика Этьена Безу (1730-1783).
Теорема 8 (теорема Безу). Остаток от деления многочлена 
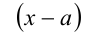
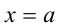
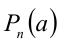
Следствие. Многочлен 
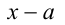
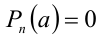
Приведённое следствие из теоремы Безу во многих случаях позволяет решать целые алгебраические уравнения 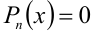
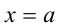

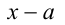
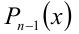
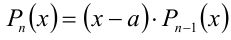
Пример №172.
Найти все значения а и b, при которых многочлен 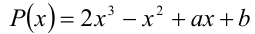
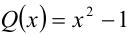
Решение:
Разложим многочлен 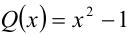
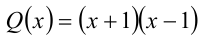
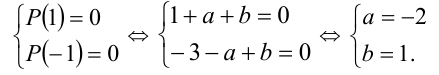
Теорема 9 (о рациональных корнях многочленов с целыми коэффи-циентами). Пусть 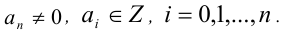
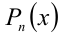
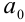
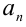
Следствие. Если 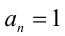
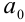
Пример №173.
Решить уравнение в целых числах
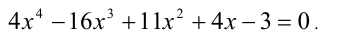
Решение:
Согласно следствию из приведённой выше теоремы, все целые корни уравнения находятся среди целых делителей свободного члена, т.е. среди чисел ± 1, ± 3 . Обозначим многочлен в левой части уравнения через f(x) . Сделаем проверку:
1) 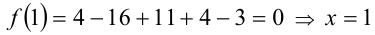
2) 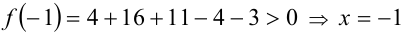
3)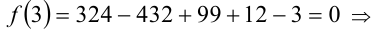
4) 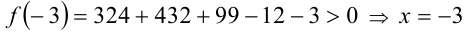
Ответ: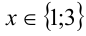
Пример №174.
Найти все корни уравнения
Решение:
Не будем сразу применять указанный выше метод, а поступим следующим образом: сделаем многочлен в левой части уравнения приведённым. Для этого положим у = 2х , тогда имеем уравнение
Обозначим через f(у) левую часть последнего уравнения. Свободный член в данном случае имеет 4 целых делителя ± 1, ± 5. Поскольку f( ± 1 )=0 и f(5)= 0, а больше трёх корней кубическое уравнение иметь не может, то это все корни этого уравнения. Выполняя обратную подстановку, находим соответствующие им три корня исходного уравнения.
Ответ:
Обратимся теперь к обобщению теоремы Виета на случай алгебраических уравнений n -й степени 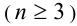
Теорема 10 (теорема Виета, общий случай). Пусть 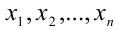
Тогда корни уравнения 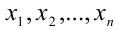
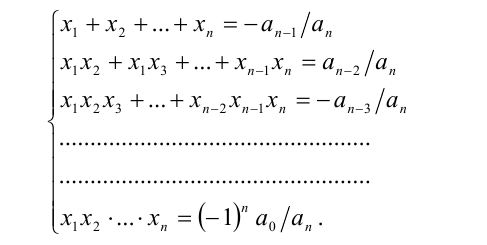
Пример №175.
Определить все значения параметра а, при каждом из которых три различных корня уравнения
образуют геометрическую прогрессию. Найти эти корни.
Решение:
По теореме Виета для кубических уравнений
в частности, имеем 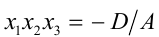
Условие того, что корни уравнения образуют геометрическую прогрессию, можно записать в виде

Из (1) и (2) следует, что 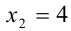
Проверка. 1) a = 0: исходное уравнение принимает вид 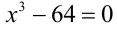
2) а = 1: имеем уравнение 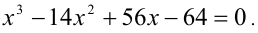
Его корни 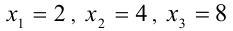
Ответ:
А теперь обратимся к рассмотрению основных видов и способов решения целых алгебраических уравнений.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Предмет математика
Эти страницы возможно вам будут полезны:
Алгебраические уравнения высших степеней с параметрами
Разделы: Математика
1.1. Общая методическая концепция решения уравнений с параметрами
Пусть дано уравнение F(x, a) = 0, (1)
если ставится задача для каждого значения а 
то уравнение (1) называется уравнением с неизвестным х и параметром а. А – область изменения параметра. Принято считать, что А – множество действительных чисел. Решить уравнение (1) – значит решить множество уравнений, которые получаются из уравнения (1) при а 
1.2. Использование параметра как равноправной переменной
Некоторые уравнения бывает целесообразно решать, рассматривая их как уравнение именно относительно параметра, который фигурирует в условии, а не относительно искомой переменной. Этот путь эффективен, в частности, в тех случаях, когда степень переменной относительно высока, а степень параметра равна двум.
Пример 1. Решить уравнение с параметром.
2x 3 – (а+2)х 2 – ах + а 2 = 0 (1)
Решение: Данное уравнение можно рассматривать как квадратное относительно параметра а, переписав его в виде:
а 2 – х(х+1)а – 2х 2 + 2х 3 = 0 (2)
Найдем дискриминант D.
D = х 2 (х+1) 2 – 8(х 3 – х 2 ) = х 4 — 6х 3 + 9х 2 = х 2 (х 2 — 6х + 9) = х 2 (х — 3) 2 .
Найдем корни уравнения (2).

Получим уравнение (а – х 2 + х)(а – 2х) = 0 равносильное исходному уравнению, которое ещё в свою очередь равносильно совокупности
Рассмотрим уравнение х 2 – х – а = 0, D = 1 – 4а.
D = 0 при а = -1/4 один корень х = 1/2
D 0 при а > -1/4 два корня
Рассмотрим уравнение х = а/2, при а = -1/4, х = -1/8.
Ответ: при а > -1/4 три корня: х1 = а/2,
при а = -1/4 два корня: х1 = -1/8; х 2 = ½
при а 4 – (а+2)х 3 – (а – 1)х 2 + (а 2 – 1) = 0;
1.3. Графический способ решения уравнений с параметрами
Взгляд на параметр как на равноправную переменную находит свое отражение в графических методах. В самом деле, поскольку параметр «равен в правах» с переменной, то ему, естественно можно выделить и свою координатную ось. Таким образом, возникает координатная плоскость (х; а). Рассмотрим примеры.
Пример 1. В зависимости от параметра а определить число корней уравнения.
x 4 – 10х 3 – 2(а — 11)х 2 + 2(5а + 6)х + 2а + а 2 = 0;
Решение. Рассмотрим это уравнение как квадратное относительно а.
а 2 + 2а(1 + 5х – х 2 ) + (х 4 – 10х 3 + 22х 2 + 12х) = 0;
D/4 = 1 + 25х 2 + х 4 + 10х – 10х 3 – 2х 2 – х 4 + 10х 3 – 22х 2 – 12х = х 2 – 2х +1 = = (х – 1) 2
Найдем а1 и а2 ; а1 = х 2 -5х – 1 + х – 1 = х 2 — 4х – 2;
а2 = х 2 -5х – 1 — х + 1 = = х 2 – 6х.
Теперь обращаемся к координатной плоскости (х; а).
х 2 — 4х – 2 = х 2 – 6х, 2х = 2, х = 1, а(1) = -5.
Ответ: если а -5, то четыре решения.
Упражнения
Найти все значения параметра а, при каждом из которых уравнение имеет три решения.
- (х 2 – 12а) 2 – 24х 2 + 32х + 96а = 0;
- (2х 2 – а) 2 – 24х 2 + 16х + 4а = 0;
- (2х 2 – а) 2 = 13х 2 + 6х – 2а = 0.
1.4. Использование свойств функций для решения алгебраических уравнений
На выпускных экзаменах за курс средней школы встречаются уравнения с параметром, решение которых связано с использованием четности функций. Напомним определение четности функции.
Определение. Функция f(x) называется четной, если f(-x) = f(x) для любого х из области определения этой функции. График четной функции симметричен относительно оси ординат. У четной функции область определения симметрична относительно начала координат.
Пример 1. Может ли при каком-нибудь значении а уравнение
2х 8 – 3ах 6 + 4х 4 – ах 2 = 5 иметь 5 корней?
Решение. Обозначим f(x) = 2х 8 – 3ах 6 + 4х 4 – ах 2 . f(x) – функция четная, поэтому, если х0 – корень данного уравнения, то – х0 – тоже, х = 0 не является корнем данного уравнения (0 ≠ 5). Следовательно, число корней у этого уравнения при любом действительном а четно, поэтому 5 корней оно иметь не может.
Пример 2. При каком значении а уравнение х 10 – а|х| + a 2 – а = 0 имеет единственное решение?
Решение. Обозначим f(x) = х 10 – а|х| + a 2 – а, f(x) – функция четная, поэтому, если х0 – корень данного уравнения, то – х0 – тоже. Значит для единственности решения необходимо, чтобы х0 = 0. В этом случае из уравнения получим: a 2 – а = 0, а = 0 или а = 1. Проверим достаточность каждого из полученных значений параметра а,
при а = 0, х 10 = 0, т.е. х = 0 единственное решение.
при а = 1, х 10 — |x| = 0. Корнями являются числа ± 1, 0.
Ответ: при а = 0 уравнение имеет единственное решение.
Упражнения
- Может ли при каком-нибудь а уравнение 2х 6 – х 4 – ах 2 = 1 иметь три корня?
- Может ли при каком-нибудь а уравнение 2х 6 – 2ах 4 + 3х 2 = 4 иметь пять корней?
- При каком значении а уравнение
имеет единственное решение?
1.5. Метод замены
Как мы уже знаем, что рациональное и быстрое решение уравнения зависит от замены переменной. Рассмотрим примеры, для решения которых нужны специальные замены, которые приводят как раз к быстрому решению уравнений.
Пример 1. Решить уравнение (х + 2а)(х +3а)(х + 8а)(х + 12а) = 4а 2 х 2 ,
где а – параметр.
Решение. Данное уравнение относится к уравнению вида
(х + а)(х +b)(х + c)(х + d) = Eх 2 (см. п. 2.5 (3))
Используя специфику решения такого уравнения, будем иметь:
(х 2 + 14ах +24а 2 )( х 2 + 11ах +24а 2 ) = 4а 2 х 2
Если а = 0, то х = 0.
Обратно, если а ≠ 0, то х ≠ 0.
Разделим обе части этого уравнения на а 2 х 2 , будем иметь
В полученном уравнении сделаем подстановку 
Таким образом, получим два уравнения

Решим первое уравнение х 2 + 15ах + 24а 2 = 0, D = 129a 2 , х1,2
Решим второе уравнение х 2 + 10ах + 24а 2 = 0, D = 4a 2
х 3 = -6а, х 4 = -4а
Ответ: если а = 0, то х = 0
если а ≠ 0, то х1,2
Упражнения
- Найдите все действительные значения величины а, при которых уравнение х(х +1)(х + а)(х + 1 + а) = а 2 имеет четыре действительных корня.
- Решить уравнение х 4 + а 4 – 3ах 3 + 3а 2 х = 0.
- При каких значениях а уравнение (х 2 – 2х) 2 — (а + 2)(х 2 – 2х) + 3а – 3 = 0 имеет четыре корня?
- Решить уравнение (х + а)(х + 2а)(х + 3а)(х + 4а) = 3а 4
Квадратные уравнения с параметром
Уравнение называется квадратным, если имеет вид (ax^2+bx+c=0,) где (a,b,c) — любые числа ((a≠0)). При этом надо быть внимательным, если (a=0), то уравнение будет линейным, а не квадратным. Поэтому, первым делом при решении квадратного уравнения с параметром, рекомендую смотреть на коэффициент при (x^2) и рассматривать 2 случая: (a=0) (линейное уравнение); (a≠0) (квадратное уравнение). Квадратное уравнение часто решается при помощи дискриминанта или теоремы Виета.
Исследование квадратного многочлена
Чтобы решить квадратное уравнение с параметром, нужно понять, при каких значениях параметра существуют корни, и найти их, выразив через параметр. Обычно это делается просто через анализ дискриминанта. (см. пример 1) Но иногда в задачах с параметром просят найти такие значения параметра, при которых корни принадлежат определенному числовому промежутку. Например:
- Найдите такие значения параметра, чтобы оба корня были меньше некоторого числа (γ): (x_1≤x_2 0)); ветки параболы направлены вниз ((a 0). Значит, между корнями функция принимает отрицательные значения, а вне этого отрезка – положительные. Так как наше число (γ) должно по условию лежать вне отрезка ((x_1,x_2)), то (f(γ)>0).
- (a 0). Этим условием мы накладываем ограничение, что наши корни должны лежать слева или справа от числа (γ).
В итоге получаем:
если (a*f(γ) 0), то (γ∉(x_1,x_2)).
Нам осталось наложить условие, чтобы наши корни были слева от числа (γ). Здесь нужно просто сравнить положение вершины нашей параболы (x_0) относительно (γ). Заметим, что вершина лежит между точками (x_1) и (x_2). Если (x_0 0, \x_0
При каких значениях параметра a уравнение $$a(a+3) x^2+(2a+6)x-3a-9=0$$ имеет более одного корня?
1 случай: Если (a(a+3)=0), то уравнение будет линейным. При (a=0) исходное уравнение превращается в (6x-9=0), корень которого (x=1,5). Таким образом, при (a=0) уравнение имеет один корень.
При (a=-3) получаем (0*x^2+0*x-0=0), корнями этого уравнения являются любые рациональные числа. Уравнение имеет бесконечное количество корней.
2 случай: Если (a≠0; a≠-3), то получим квадратное уравнение. При положительном дискриминанте уравнение будет иметь более одного корня: $$D>0$$ $$D/4=(a+3)^2+3a(a+3)^2>0$$ $$(a+3)^2 (3a+1)>0$$ $$a>-frac<1><3>.$$ С учетом (a≠0;) (a≠-3), получим, что уравнение имеет два корня при (a∈(-frac<1><3>;0)∪(0;+∞)). Объединив оба случая получим (внимательно прочитайте, что от нас требуется):
Найти все значения параметра a, при которых корни уравнения $$(a+1) x^2-(a^2+2a)x-a-1=0$$ принадлежат отрезку ([-2;2]).
1 случай: Если (a=-1), то (0*x^2-x+1-1=0) отсюда (x=0). Это решение принадлежит ([-2;2]).
2 случай: При (a≠-1), получаем квадратное уравнение, с условием, что все корни принадлежат ([-2;2]). Для решения введем функцию (f(x)=(a+1) x^2-(a^2+2a)x-a-1) и запишем систему, которая задает требуемые условия:
Подставляем полученные выражения в систему:
Параметрические уравнения, неравенства и системы, часть С
Теория к заданию 18 из ЕГЭ по математике (профильной)
Параметрические уравнения
Уравнение, которое кроме неизвестной величины содержит также другую дополнительную величину, которая может принимать различные значения из некоторой области, называется параметрическим. Эта дополнительная величина в уравнении называется параметр. На самом деле с каждым параметрическим уравнением может быть написано множество уравнений.
Способ решения параметрических уравнений
- Находим область определения уравнения.
- Выражаем a как функцию от $х$.
- В системе координат $хОа$ строим график функции, $а=f(х)$ для тех значений $х$, которые входят в область определения данного уравнения.
- Находим точки пересечения прямой, $а=с$, где $с∈(-∞;+∞)$ с графиком функции $а=f(х)$. Если прямая, а=с пересекает график, $а=f(х)$, то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение вида, $а=f(х)$ относительно $х$.
- Записываем ответ.
Общий вид уравнения с одним параметром таков:
При различных значениях, а уравнение $F(x, a) = 0$ может иметь различные множества корней, задача состоит в том, чтобы изучить все случаи, выяснить, что будет при любом значении параметра. При решении уравнений с параметром обычно приходится рассматривать много различных вариантов. Своевременное обнаружение хотя бы части невозможных вариантов имеет большое значение, так как освобождает от лишней работы.
Поэтому при решении уравнения $F(x, a) = 0$ целесообразно под ОДЗ понимать область допустимых значений неизвестного и параметра, то есть множество всех пар чисел ($х, а$), при которых определена (имеет смысл) функция двух переменных $F(x, а)$. Отсюда естественная геометрическая иллюстрация ОДЗ в виде некоторой области плоскости $хОа$.
ОДЗ различных выражений (под выражением будем понимать буквенно — числовую запись):
1. Выражение, стоящее в знаменателе, не должно равняться нулю.
2. Подкоренное выражение должно быть неотрицательным.
3. Подкоренное выражение, стоящее в знаменателе, должно быть положительным.
4. У логарифма: подлогарифмическое выражение должно быть положительным; основание должно быть положительным; основание не может равняться единице.
Алгебраический способ решения квадратных уравнений с параметром $ax^2+bx+c=0$
Квадратное уравнение $ax^2+bx+c=0, а≠0$ не имеет решений, если $D 0$;
Квадратное уравнение имеет один корень, если $D=0$
Тригонометрические тождества
3. $sin^<2>α+cos^<2>α=1$ (Основное тригонометрическое тождество)
Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса
http://sigma-center.ru/quadratic_equation_parametr
http://examer.ru/ege_po_matematike/teoriya/parametricheskie_uravneniya
многочлены — Найти параметр
|
Найти р,при котором x^3-px+1 делится на x^2+x+p
задан Верик 0% принятых |
Здравствуйте
Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Присоединяйтесь!
отмечен:
многочлены
×541
задан
17 Мар ’14 13:30
показан
886 раз
обновлен
17 Мар ’14 15:37
Связанные исследования
Связанные вопросы
Отслеживать вопрос
по почте:
Зарегистрировавшись, вы сможете подписаться на любые обновления
по RSS:
Ответы
Ответы и Комментарии
Многочлен и матрица как аргумент
| Исходный полином f(x) (его коэффициенты) |
| Аргумент является квадратной матрицей с элементами |
| Многочлен |
| Переменная x= |
| Результат вычислений |
Расссмотрим в данном материале одну из трудоёмких задач в высшей математике, которая звучит так: Найти чему задан многочлен
если аргумент есть квадратная матрица, то есть
И если сам принцип вычисления понятен, особенно если вы в совершенстве поняли как умножать матрицы, то непосредственное вычисление, для меня лично считается рутиной, которую по возможности нужно избежать.
Сразу хотелось бы сказать, где этот калькулятор пригодится. Для учителей, преподавателей, для создателей учебников, для тех, кому необходимо создавать оригинальные задачи по данной теме.
Также пригодится для студентов или аспирантов которые пишут рефераты, курсовые, дипломы.
Для всех остальных, это легкий способ проверить ошибку в заданном примере, решить, без долгих промежуточных вычислений, поставленную задачу.
Когда калькулятор был написан, оказалось что сайты, которые были посвещенны этой теме, содержали ошибки в промежуточных вычислениях и как как результат были неверные.
Данный калькулятор, я надеюсь избавлен от ошибок и Вы сможете безопасно решать любые примеры.
Как и подавляющее большинство калькуляторов на этом сайте, значениями как коэффициентов полинома, так и элементов матрицы, могут быть комплексные значения.
Такого на конец 2017 года, больше нигде не найдете, не считая конечно специальных созданных математических программ.
Приступим к примерам?
Найти значение полинома =2x^2-3x+4)
Еще один пример
Чему равен полином =ix^5+(2-i)x^2-11x)
Найти значение многочлена =x^4-x-1)
Удачный расчетов !
Многочленом п-ой степени от неизвестного х называется выражение
вида
a0 xn + a1xn−1 +… + an−1x + an ,
представляющее собой сумму целых неотрицательных степеней неизвестного х, взятых с некоторыми числовыми коэффициентами. Помимо записи многочлена по убывающим степеням неизвестного х, допустимы и другие записи, получающиеся перестановкой слагаемых, например, запись по
возрастающим степеням неизвестного. Многочлен называется приведенным к стандартному или каноническому виду, если он записан строго по
|
убывающим степеням неизвестного. |
Например, многочлен x10 + 5x6 − 3x2 +1 |
|||||||
|
является многочленом, записанным в каноническом (стандартном) виде. |
||||||||
|
Степенью многочлена называется старшая степень при неизвестном. |
||||||||
|
НапримерU |
,U многочлен x2 − 3x − 2 — второй степени, многочлен x5 − 3x2 + 6x8 |
— |
||||||
|
восьмой степени (запись этого многочлена не канонического вида). |
||||||||
|
Многочленом нулевой степени называется любое отличное от нуля |
||||||||
|
комплексное число. |
||||||||
|
Число нуль считается многочленом, степень которого не определена |
||||||||
|
(это единственный многочлен с неопределенной степенью). |
||||||||
|
Многочлен, степень которого равна единице называется линейным. |
||||||||
|
НапримерU |
,U число 5 – |
многочлен нулевой степени, |
многочлен |
5x − 3 |
— |
|||
|
первой степени, т.е. линейный. Линейный многочлен |
вида (x − a) |
будем |
||||||
|
называть двучленом. |
x6 − x3 + 5x |
2x2 − 7x8 +10x10 |
||||||
|
НапримерU |
,U |
выражения вида |
или |
— |
||||
|
многочлены, однако 2x2 − 1 |
+ 3 и ax−1 + bx−1 + cx−1 + d + ex + fx2 — не являются |
|||||||
|
многочленами. |
x |
|||||||
|
Для сокращенной записи многочленов употребляются символы f (x) , |
||||||||
|
g(x) , ϕ(x) , P(x) , Q(x) , …. |
||||||||
|
Два многочлена f (x) |
и g(x) считаются равными (или тождественно |
|||||||
|
равными) |
f (x) |
= |
g(x) , в |
том и |
только в том |
случае, если равны их |
коэффициенты при одинаковых степенях неизвестного.
49
3.1 Действия над многочленами
1 Операция сложения
Пусть даны многочлены с комплексными коэффициентами f (x) = a0 + a1x + … + an−1xn−1 + an xn , an ≠ 0 ,
|
g(x) = b |
+ b x + … + b |
xs −1 |
+ b xs , b |
≠ 0 |
(3.1) |
|||||
|
0 |
1 |
s −1 |
s |
s |
||||||
|
(для определенности пусть n > s ) |
||||||||||
|
Суммой многочленов |
f (x) и g(x) называется многочлен |
|||||||||
|
f (x) + g(x) = c |
0 |
+ c x + … + c |
n −1 |
xn −1 |
+ c |
n |
xn , |
(3.2) |
||
|
1 |
коэффициенты которого есть сумма коэффициентов многочленов f (x) и g(x) ,
|
стоящих |
при |
одинаковых степенях неизвестного, |
т.е. ci = ai + bi , |
i = 0, 1,…, n |
|
причем |
при |
n > s коэффициенты bs +1 , bs +2 , …, |
bn равны нулю. |
Очевидно, |
степень суммы равна п, при n > s , но при n = s степень многочлена (3.2) может
|
оказаться меньше п, в случае если bn = −an . |
f (x) = 2 + 7x2 − 3x6 |
||
|
НапримерU |
,U |
найдем сумму многочленов |
и |
g(x) = 4 − 2x2 + 3x6 .
f (x) + g(x) = 6 + 5x2 .
Мы получили, что суммой многочленов шестой степени оказался многочлен второй степени.
Произведение многочленов
|
Произведением многочленов f (x) |
и |
g(x) |
называется |
многочлен |
|||||
|
f (x) g(x) = d |
0 |
+ d x + … + d |
n+s −1 |
xn+s −1 + d |
n+s |
xn+s , |
(3.3) |
||
|
1 |
|||||||||
|
коэффициенты которого определяются следующим образом: |
|||||||||
|
di = ∑ak bl , i = 0,1,…, n + s −1, n + s , |
(3.4) |
||||||||
|
k +l =i |
|||||||||
|
т.е. коэффициент di |
есть результат перемножения коэффициентов многочленов |
||||||||
|
f (x) и g(x) , сумма индексов которых |
равна |
i , и |
сложения |
всех таких |
|||||
|
произведений; |
в |
частности, |
d0 = a0b0 , |
d1 = a0b1 + a1b0 , …, dn+s = anbs . Из |
последнего равенства следует, что dn+s ≠ 0 и поэтому степень произведения двух
многочленов равна сумме степеней этих многочленов.
Отсюда следует, что произведение многочленов, отличных от нуля, никогда не будет равным нулю.
Найдем произведения многочленов f (x) и g(x) предыдущего примера f (x) g(x) = (2 + 7x2 − 3x6 ) (4 − 2x2 + 3x6 )=8 − 4x2 + 6x6 + 28x2 −14x4 +
+ 21x8 −12x6 + 6x8 − 9x12 = −9x12 + 27x8 − 6x6 −14x4 − 4x2 + 8 — многочлен 12-й
степени.
50
Свойства операций сложения и произведения произвольных многочленов
Коммутативность и ассоциативность сложения немедленно вытекают из справедливости этих свойств для сложения чисел, так как складываются коэффициенты при каждой степени неизвестного отдельно.
Операция вычитания также выполнима на множестве многочленов: роль нуля играет число нуль, включенное нами в число многочленов, а противоположным для записанного выше многочлена f (x) будет многочлен
− f (x) = −a0 − a1x −… − an −1xn −1 − an xn .
Коммутативность умножения вытекает из коммутативности умножения чисел и того факта, что в определении произведения многочленов коэффициенты обоих множителей f (x) и g(x) используются равноправным образом.
Ассоциативность умножения доказывается следующим образом: если, помимо записанных выше многочленов f (x) и g(x) , дан еще многочлен
|
h(x) = c |
0 |
+ c x +… + c |
i −1 |
xi −1 |
+ c |
xi , c |
i |
≠ 0 , |
|||
|
1 |
i |
[f (x)g(x)]h(x) |
|||||||||
|
то коэффициентом |
при |
xi , |
i = 0, 1, …, n + s + t в произведении |
||||||||
|
будет служить число |
|||||||||||
|
= |
∑ak bl cm , |
||||||||||
|
∑ |
∑ak bl cm |
||||||||||
|
j +m=i k +l =i |
k +l +m=i |
||||||||||
|
и в произведении |
f (x)[g(x)h(x)] — равное ему число |
||||||||||
|
∑ ak |
∑ak bl cm . |
||||||||||
|
∑bl cm = |
|||||||||||
|
k + j =i |
l +m=i |
k +l +m=i |
|||||||||
|
Наконец, справедливость закона дистрибутивности вытекает из равенства |
|||||||||||
|
∑(ak + bk )ci = ∑ak cl + ∑bk ci , |
|||||||||||
|
k +l =i |
k +l =i |
k +l =i |
|||||||||
|
так как левая часть этого равенства является коэффициентом при xi |
в многочлене |
||||||||||
|
[f (x) + g(x)]h(x) , |
а |
правая часть – коэффициентом при той же степени |
|||||||||
|
неизвестного в многочлене |
f (x)h(x) + g(x)h(x) . |
||||||||||
|
Роль единицы при умножении многочленов играет число 1, |
|||||||||||
|
рассматриваемое как многочлен нулевой степени. |
|||||||||||
|
Существование многочлена обратного данному |
|||||||||||
|
Многочлен |
f (x) тогда и только тогда обладает обратным многочленом |
||||||||||
|
f −1(x) , т.е. выполнено равенство |
|||||||||||
|
f (x) f −1 (x) =1, |
(3.5) |
||||||||||
|
когда f (x) является многочленом нулевой степени. |
51

Действительно, если f (x) является отличным от нуля числом а, то обратным многочленом служит для него число a−1 . Если же f (x) имеет степень n ≥1, то степень левой части равенства (3.5), если бы многочлен f −1(x)
существовал, была бы не меньше п, в то время как справа стоит многочлен нулевой степени.
Отсюда вытекает, что многочлен, обратный данному, вообще говоря не существует. В этом отношении система всех многочленов с комплексными коэффициентами напоминает систему всех целых чисел. Эта аналогия проявляется и в том, что для многочленов, как и для целых чисел, существует алгоритм деления с остатком.
Деление многочленов
Большую роль в доказательстве и получении разнообразных алгебраических результатов играет деление многочленов с остатком. Разделить многочлен f (x) на многочлен g(x) означает подобрать такую пару многочленов
q(x) и r(x) , что f (x) = q(x)g(x) + r(x) как и при делении чисел f (x) — делимое, g(x) — делитель; q(x) — частное, r(x) — остаток. Практический алгоритм
|
нахождения делителя, частного и остатка – деление |
f (x) на g(x) столбиком. |
|
|
Теорема 3.1 Для любых двух многочленов |
f (x) и |
g(x) можно найти |
|
такие многочлены q(x) и r(x) , что f (x) = g(x)q(x) + r(x) , |
(3.6) |
причем степень r(x) меньше степени g(x) или же r(x) = 0 . Многочлены q(x) и r(x) , удовлетворяющие этому условию (3.6), определяются однозначно.
Доказательство. Докажем сначала вторую половину теоремы. Пусть
существуют еще многочлены q(x) и r(x) также удовлетворяющие равенству
|
(3.6), т.е. |
|
|
f (x) = g(x)q(x) + r(x) , |
(3.7) |
причем степень r(x) снова меньше степени g(x) . Приравнивая друг другу правые части равенств (3.6) и (3.7), получим:
g( x )(q( x ) − q( x ))= r( x ) − r( x ) .
Степень правой части этого равенства меньше степени g(x) , степень же левой части была бы при q(x) − q(x) ≠ 0 больше или равна степени g(x) . Поэтому должно быть q(x) − q(x) = 0 , т.е. q(x) = q(x) , а тогда и r(x) = r(x) . Что и
требовалось доказать.
Переходим к доказательству первой половины теоремы. Пусть многочлены f (x) и g(x) имеют соответственно степени п и s . Если n < s , то
можно положить q(x) = 0 , r(x) = f (x) . Если же n ≥ s , то воспользуемся тем же
методом, каким производится деление многочленов с действительными коэффициентами, расположенными по убывающим степеням неизвестного. Пусть
f (x) = a0 xn + a1xn−1 +… + an−1x + an , a0 ≠ 0 ,
52
|
g(x) = b xs + b xs −1 |
+… + b |
x + b , |
b ≠ 0 . |
||||
|
0 |
1 |
a0 |
s −1 |
s |
0 |
||
|
Полагая |
f (x) − |
xn−s g(x) = f (x) , |
(3.8) |
||||
|
b0 |
1 |
||||||
мы получим многочлен, степень которого меньше п. Обозначим эту степень через
|
n1 , а старший коэффициент многочлена f1(x) |
— через a1,0 . Положим, далее, если |
||||||||||||
|
все еще n1 ≥ s , |
|||||||||||||
|
f1 (x) − |
a1,0 |
xn1 −s g(x) = f2 (x) , |
(3.8)1B B |
||||||||||
|
b0 |
степень, а через a2,0 |
||||||||||||
|
обозначим через n2 — |
— |
старший коэффициент многочлена |
|||||||||||
|
f2 (x) , положим затем |
|||||||||||||
|
a2,0 |
n −s |
g(x) = f3 (x) , |
(3.8)2B B |
||||||||||
|
f2 (x) − |
x 2 |
||||||||||||
|
b0 |
|||||||||||||
|
и т.д. |
|||||||||||||
|
f2 (x), … убывают, |
n > n1 > n2 >…, то |
||||||||||||
|
Так как степени многочленов f1(x), |
|||||||||||||
|
мы дойдем после конечного числа шагов до такого многочлена |
fk (x) , |
||||||||||||
|
fk −1(x) − |
ak −1,0 |
x |
n |
k −1 |
−s |
g(x) = fk (x) |
(3.8)kB -1B |
||||||
|
b0 |
|||||||||||||
степень которого nk меньше s , после чего наш процесс останавливается. Складывая теперь равенства (3.8), (3.8)1B ,B …, (3.8)kB -1,B мы получим:
|
a |
0 |
n−s |
a1,0 |
n |
−s |
ak −1, 0 |
n |
−s |
||||||||||||||||
|
1 |
k −1 |
|||||||||||||||||||||||
|
f (x) − |
x |
+ |
x |
+… |
+ |
x |
g(x) = fn (x) , |
|||||||||||||||||
|
b |
b |
b |
||||||||||||||||||||||
|
0 |
0 |
0 |
||||||||||||||||||||||
|
т.е. многочлены |
a1,0 |
ak −1, 0 |
||||||||||||||||||||||
|
a |
0 |
n−s |
n −s |
n |
−s |
|||||||||||||||||||
|
q(x) = |
x |
+ |
x 1 |
+… + |
x |
k −1 |
, |
|||||||||||||||||
|
b |
b |
b |
||||||||||||||||||||||
|
0 |
0 |
0 |
r(x) = fk (x)
действительно удовлетворяют равенству (3.6), причем степень r(x) на самом деле меньше степени g(x) , что и требовалось доказать.
Заметим, что если многочлены f (x) и g(x) с целыми коэффициентами и старший коэффициент многочлена g(x) равен единице, то многочлены q(x) и r(x) будут иметь только целые коэффициенты. При делении столбиком придется умножать многочлен g(x) лишь на целые кратные степеней переменной х.
Отметим также, что при делении на многочлен первой степени остаток является константой.
53
3.2 Свойства делимости многочленов
Пусть f (x) и ϕ(x) — ненулевые многочлены, тогда многочлен f (x) делится нацело на многочлен ϕ(x) , если остаток от деления f (x) на ϕ(x) равен
нулю.
В этом случае многочлен ϕ(x) называется делителем многочлена f (x) .
Теорема 3.2 Многочлен ϕ(x) тогда и только тогда будет делителем многочлена f (x) , если существует многочлен ψ (x) , удовлетворяющий равенству
|
f (x) =ϕ(x)ψ (x) . |
(3.9) |
|
Доказательство. Если ϕ(x) является делителем для |
f (x) , то в качестве |
|
ψ (x) следует взять частное от деления f (x) на ϕ(x) . |
Обратно, пусть многочлен ψ (x) , удовлетворяющий равенству (3.9), существует. Из доказанной ранее единственности многочленов q(x) и r(x) , удовлетворяющих равенству f (x) =ϕ(x)q(x) + r(x) и условию, что степень r(x) меньше степени ϕ(x) , в нашем случае следует, что частное от деления f (x) на ϕ(x) равно ψ (x) , а остаток равен нулю.
Очевидно, что если f (x) =ϕ(x)ψ (x) , то делителем для f (x) будет как ϕ(x) , так и ψ (x) и что степени ϕ(x) и ψ (x) не могут быть больше степени f (x) .
Очевидно, что если многочлен f (x) и его делитель ϕ(x) имеют оба рациональные или действительные коэффициенты, то и многочлен ψ (x) также
будет иметь рациональные, или, соответственно, действительные коэффициенты, так как он разыскивается при помощи алгоритма деления.
Основные свойства делимости многочленов
1. Если f (x) делится на g(x) , а g(x) делится на h(x) , то f (x) будет делится на h(x) .
В самом деле, по условию f (x) = g(x)ϕ(x) и g(x) = h(x)ψ (x) , а поэтому
f(x) = h(x)[ϕ(x)ψ (x)].
2.Если f (x) и g(x) делятся на ϕ(x) , то их сумма и разность также делятся на ϕ(x) .
|
Действительно, из равенства f (x) =ϕ(x)ψ (x) и |
g(x) =ϕ(x)χ(x) вытекает |
|
f (x) ± g(x) =ϕ(x)[ψ (x) ± χ(x)]. |
|
|
3. Если f (x) делится на ϕ(x) , то произведение |
f (x) на любой многочлен |
|
g(x) также будет делиться на ϕ(x) . |
|
|
Действительно, если f (x) =ϕ(x)ψ (x) , то f (x)g(x) =ϕ(x)[ψ (x)g(x)]. |
|
|
Из 2 и 3 вытекает следующее свойство: |
fk (x) делится на ϕ(x) , то |
|
4. Если каждый из многочленов f1(x), f2 (x), …, |
на ϕ(x) будет делиться и многочлен f1(x)g1(x) + f2 (x)g2 (x) + … + fk (x)gk (x) , где g1(x), g2 (x), …, gk (x) — произвольные многочлены.
54
|
5. Всякий многочлен |
f (x) делится на любой многочлен нулевой степени. |
||||||||||||||||||||
|
Действительно, |
если |
f (x) = a |
0 |
xn + a xn−1 |
+… + a |
n |
−1 |
x + a |
n |
, |
а |
с — |
|||||||||
|
1 |
|||||||||||||||||||||
|
произвольное число, |
не равное |
нулю, т.е. произвольный |
многочлен |
нулевой |
|||||||||||||||||
|
a |
0 |
a |
a |
n |
|||||||||||||||||
|
степени, то f (x) = c |
xn + |
1 |
xn−1 +… + |
. |
|||||||||||||||||
|
c |
c |
||||||||||||||||||||
|
6. |
c |
||||||||||||||||||||
|
Если f (x) |
делится на |
ϕ(x) , то |
f (x) делится и на cϕ(x) , |
где с – |
|||||||||||||||||
|
произвольное число, отличное от нуля. |
f (x) =ϕ(x)ψ (x) |
следует |
равенство |
||||||||||||||||||
|
В |
самом |
деле, |
из |
равенства |
|||||||||||||||||
|
f (x) = [cϕ(x)] [c−1ψ (x)]. |
|||||||||||||||||||||
|
7. Многочлены cf (x) , |
c ≠ 0 , и только они, будут делителями многочлена |
||||||||||||||||||||
|
f (x) , имеющими такую же степень, что и f (x) . |
|||||||||||||||||||||
|
Действительно, |
f (x) = c−1[cf (x)], т.е. |
f (x) делится на cf (x) . |
|||||||||||||||||||
|
Если, с другой стороны, |
f (x) делится на ϕ(x) , причем степени |
f (x) и |
|||||||||||||||||||
|
ϕ(x) совпадают, то степень частного от деления |
f (x) |
на |
ϕ(x) |
должна быть |
|||||||||||||||||
|
равной нулю, т.е. |
f (x) = dϕ(x) , d ≠ 0 , откуда ϕ(x) = d −1 f (x) . |
||||||||||||||||||||
|
Отсюда вытекает следующее свойство: |
|||||||||||||||||||||
|
8. |
Тогда и только тогда многочлены f (x) , |
g(x) |
одновременно делятся |
||||||||||||||||||
|
друг на друга, если g(x) = cf (x) , c ≠ 0 . |
|||||||||||||||||||||
|
Наконец, из 8 и 1 вытекает свойство |
|||||||||||||||||||||
|
9. |
Всякий делитель одного из двух многочленов |
f (x) , cf (x) , |
где c ≠ 0 , |
будет делителем и для другого многочлена.
Процесс деления многочленов «столбиком» рассмотрим на практических занятиях (см. тему «Многочлены»).
3.3 Корни многочлена. Теорема Безу
Значением многочлена
|
f (x) = a |
0 |
xn + a xn−1 |
+… + a |
n |
(3.10) |
|||||||||
|
1 |
cn + a cn−1 |
|||||||||||||
|
при x = c называется результат вычисления a |
0 |
+ … + a |
n |
. |
||||||||||
|
1 |
||||||||||||||
|
НапримерU |
,U найти значения многочлена |
f (x) = x2 − 3x +1, при x = 0 , |
x = 2. |
|||||||||||
|
Вместо переменной подставляем в выражение |
f (x) |
заданные x = 0 , |
x = 2 и |
|||||||||||
|
производим |
соответствующие |
вычисления, |
т.е. |
f (0) = 02 − 3 0 +1, |
f (0) =1, |
|||||||||
|
аналогично |
f (2) = 22 − 3 2 +1, f (2) = 0 . |
|||||||||||||
|
Т.е. значение заданного многочлена при x = 0 равно единице, при x = 2 — |
||||||||||||||
|
нулю. |
ϕ(x) = f (x) + g(x) , |
ψ (x) = f (x)g(x) , |
то |
|||||||||||
|
Очевидно, |
что |
если |
||||||||||||
|
ϕ(c) = f (c) + g(c) , ψ (c) = f (c) g(c) . |
||||||||||||||
|
Корнем многочлена |
f (x) |
называется такое x = c , при котором значение |
||||||||||||
|
многочлена равно нулю. |
55
|
Таким образом, в примере разобранном |
выше x = 2 является |
корнем |
|||||||
|
многочлена |
f (x) = x2 − 3x +1. |
||||||||
|
Важную роль в процессе нахождения корней многочлена играет теорема |
|||||||||
|
Безу и ее следствия. |
|||||||||
|
Теорема Безу. Число x0 тогда и только |
тогда |
является |
корнем |
||||||
|
многочлена |
f (x) , |
когда |
существует |
такой |
многочлен |
q(x) , |
что |
||
|
f (x) = (x − x0 )q(x) . |
для f (x) , |
то, |
|||||||
|
Доказательство. Если имеет место такое |
представление |
||||||||
|
подставляя в него x = x0 , получим: f (x0 ) = 0 . |
f (x) . Разделим многочлен |
f (x) на |
|||||||
|
Обратно, пусть x0 — корень многочлена |
|||||||||
|
многочлен |
x − x0 : |
f (x) = q(x)(x − x0 ) + r . Здесь r |
— действительное число. |
Оно |
|||||
|
равно нулю. В |
самом |
деле, подставим |
в |
это |
равенство |
x = x0 : |
|||
|
0 = f (x0 ) = q(x0 )(x0 − x0 ) + r r = 0 . |
Следствия теоремы Безу:
1 Остаток от деления многочлена f (x) на двучлен (x − c) равен значению
|
многочлена при x = c , то есть r = f (c) . |
|||||||||||||||||
|
2 При делении многочлена |
f (x) |
на двучлен |
вида |
ax + b |
получается |
||||||||||||
|
остаток, равный значению этого многочлена при x = − |
b |
, т.е. |
− |
b |
|||||||||||||
|
a |
r = f |
. |
|||||||||||||||
|
a |
|||||||||||||||||
|
НапримерU |
,U используя второе следствие из теоремы Безу найдем остаток от |
||||||||||||||||
|
деления многочлена |
f (x) = 2x3 − x2 + 4x −1 на двучлен 2x −1. |
||||||||||||||||
|
Решение. |
1 |
1 3 |
1 2 |
1 |
. Таким образом, искомый |
||||||||||||
|
r = |
f |
= 2 |
− |
+ 4 |
−1 =1 |
||||||||||||
|
2 |
2 |
2 |
2 |
остаток равен единице.
Использование теоремы Безу в задачах разложения многочлена на множители подробно рассматривается в практических разработках.
Как мы отметили выше, деление многочлена на многочлен производится как «обычное» деление, т.е. столбиком. Существует метод Горнера, дающий возможность достаточно несложным образом разделить многочлены любой степени на многочлен первой степени, т.е. на двучлен.
3.4 Метод Горнера
Пусть дан многочлен
|
f (x) = a |
0 |
xn + a xn−1 + a |
2 |
xn−2 +… + a |
n |
(3.11) |
|
|
1 |
|||||||
|
и пусть результат его деления на двучлен (x − c) есть |
|||||||
|
f (x) = (x − c)q(x) + r , |
(3.12) |
||||||
|
где q(x) = b xn−1 + b xn−2 |
+ b xn−3 + … + b |
. |
|||||
|
0 |
1 |
2 |
n −1 |
Сравнивая коэффициенты при одинаковых степенях xi в (3.12), получаем:
56

a0 = b0 ,
a1 = b1 − cb0 , a2 = b2 − cb1 ,
…………..
an−1 = bn−1 − cbn−2 , an = r − cbn −1 .
Отсюда следует, что b0 = a0 , bk = cbk −1 + ak , k =1, 2,…, n −1, т.е. коэффициенты bk получается умножением предыдущего коэффициента ak ;
наконец, r = cbn −1 + an , т.е. и остаток r , равный, как мы знаем, f (c) , получается
по этому же закону. Таким образом, коэффициенты частного и остаток можно последовательно получать при помощи однотипных вычислений, которые располагаются в схему, называемую схемой Горнера.
Для нахождения коэффициентов bn −1 , bn−2 , …, b1 , b0 и остатка r схема Горнера выглядит следующим образом:
|
a0 |
a1 |
a2 |
a3 |
… an −1 |
an |
|
|
+ |
+ |
+ |
… + |
+ |
||
|
сb0 |
сb1 |
сb2 |
… сbn−2 сbn −1 |
|||
|
с |
b0 |
b1 |
b2 |
b3 |
… bn −1 |
r |
В этой схеме, начиная с коэффициента b1 , каждое число третей строки
получается из предыдущего числа этой строки умножением на число c и прибавлением к полученному результату соответствующего числа первой строки,
|
стоящего над искомым числом. |
||||||||||
|
НапримерU |
,U |
используя |
схему |
Горнера, |
разделим |
многочлен |
||||
|
2x2 − 3x3 − x + x5 +1 на x +1. |
||||||||||
|
Сначала запишем делимое в каноническом виде, то есть в виде |
||||||||||
|
x5 + 0 x4 − 3x3 + 2x2 − x +1. |
||||||||||
|
Так как в нашем случае (x − c) = (x +1) , то c = −1. |
||||||||||
|
Применяя схему Горнера, имеем |
||||||||||
|
1 |
0 |
–3 |
2 |
–1 |
1 |
|||||
|
+ |
+ |
+ |
+ |
+ |
||||||
|
–1 |
1 |
2 |
–4 |
5 |
||||||
|
–1 |
1 |
–1 |
–2 |
4 |
–5 |
6 |
Итак, получим частное q(x) = x4 − x3 − 2x2 + 4x − 5 , остаток r = 6 . Таким образом, x5 − 3x3 + 2x2 − x +1 = (x +1)(x4 − x3 − 2x2 + 4x − 5) + 6 .
Метод деления многочлена на двучлен с использованием схемы Горнера носит название метода Горнера.
3.5 Основная теорема алгебры
57
Занимаясь в предыдущем параграфе корнями многочленов, мы не ставили вопроса о том, всякий ли многочлен обладает корнями. Известно, что существуют многочлены с действительными коэффициентами, не имеющие действительных
корней; x2 +1 — один из таких многочленов. Можно было бы ожидать, что существуют многочлены, не имеющие корней даже среди комплексных чисел, особенно если рассматриваются многочлены с любыми комплексными коэффициентами. Если бы это было так, то система комплексных чисел нуждалась бы в дальнейшем расширении. На самом деле, однако, справедлива следующая основная теорема алгебры:
Всякий многочлен с любыми числовыми коэффициентами, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный.
Эта теорема является одним из крупнейших достижений всей математики и находит применения в самых различных областях науки. На ней основана, в частности, вся дальнейшая теория многочленов с числовыми коэффициентами, и потому эту теорему называли раньше (а иногда называют и теперь) «основной теоремой высшей алгебры». В действительности, однако, основная теорема не является чисто алгебраической. Все ее доказательства, — а их, после Гаусса, впервые доказавшего эту теорему в конце XVIII века, было найдено очень много, — используют в большей или меньшей мере так называемые топологические свойства действительных и комплексных чисел, т. е. свойства, связанные с непрерывностью.
3.6 Следствия из основной теоремы алгебры
Пусть дан многочлен n -й степени, n ≥1,
|
f (x)= a |
0 |
xn + a xn−1 |
+… + a |
n−1 |
x + a |
n |
(3.13) |
|
1 |
с любыми комплексными коэффициентами. Основная теорема о существовании корня позволяет утверждать существование для f (x) корня α1 комплексного или
действительного. Поэтому многочлен f (x) обладает разложением
f (x)= (x −α1 )ϕ(x).
Коэффициенты многочлена ϕ(x) снова являются действительными или комплексными числами, и поэтому ϕ(x) обладает корнем α2 , откуда
f (x)= (x −α1 )(x −α2 )ψ (x).
Продолжая так далее, мы придем после конечного числа шагов к разложению многочлена n -й степени в произведение n линейных множителей,
|
f (x)= a0 (x −α1 )(x −α2 )…(x −αn ). |
(3.14) |
|
Коэффициент a0 появился по следующей причине: если бы |
справа в |
выражении (3.14) стоял некоторый коэффициент b, то после раскрытия скобок старший член многочлена f (x) имел бы вид bx , хотя па самом деле, ввиду (3.13),
им является член a0 xn . Поэтому b = a0 .
58
f (x)ϕ(x)= g(x)ϕ(x)
|
Разложение (3.14) является для многочлена f (x) |
единственным, с |
|
точностью до порядка сомножителей, разложением такого типа. |
|
|
Пусть, в самом деле, имеется еще разложение |
|
|
f (x)= a0 (x − β1 )(x − β2 )…(x − βn ). |
(3.15) |
|
Из (3.14) и (3.15) следует равенство |
|
|
(x −α1 )(x −α2 )…(x −αn )= (x − β1 )(x − β2 )…(x − βn ). |
(3.16) |
Если бы корень αi был отличен от всех β j , j =1, 2, …, n , то, подставляя αi вместо неизвестного в (3.16), мы получили бы слева нуль, а справа число,
отличное от нуля. Таким образом, всякий корень αi равен некоторому корню β j
и обратно.
Отсюда еще не вытекает совпадение разложений (3.14) и (3.15). Действительно, среди корней αi , i =1, 2,…, n , могут быть равные между собой.
Пусть, например, s этих корней равны α1 и пусть, с другой стороны, среди корней β j , j =1, 2, …, n , содержится t равных корню α1 . Нужно показать, что
s = t .
Так как степень произведения многочленов равна сумме степеней сомножителей, то произведение двух многочленов, отличных от нуля, не может равняться нулю. Отсюда вытекает, что если два произведения многочленов равны друг другу, то обе части равенства можно сократить на общий множитель:
если
и ϕ(x)≠ 0 , то из
[f (x)− g(x)]ϕ(x)= 0 ,
следует f (x)− g(x)= 0 , т.е. f (x)= g(x).
Применим это к равенству (3.16). Если, например, s > t то, сокращая обе части равенства (3.16) на множитель (x −α1 )t , мы придем к равенству, левая часть которого еще содержит множитель x −α1 , а правая его не содержит. Выше
показано, однако, что это приводит к противоречию. Таким образом, единственность разложения (3.14) для многочлена f (x) доказана.
Объединяя вместе одинаковые множители, разложение (3.14) можно
|
переписать в виде |
|||||||||
|
f (x)= a |
0 |
(x − α )k1 |
(x − α |
2 |
)k2 |
…(x − α |
l |
)ki , |
(3.17) |
|
1 |
|||||||||
|
где k1 + k2 + … + kn = n . |
|||||||||
|
При этом предполагается, что среди корней α1 , α2 , …, αl |
уже нет равных. |
||||||||
|
Всякий |
многочлен |
f (x) |
степени n , n ≥1, |
с любыми числовыми |
коэффициентами имеет n корней, если каждый из корней считать столько раз, какова его кратность.
Заметим, что утверждение справедливо и при n = 0 , так как многочлен нулевой степени не имеет корней. Это утверждение неприменимо лишь к многочлену 0, не имеющему степени и равному нулю при любом значении х.
59

Теорема 3.3 Если многочлены f (x) и g(x), степени которых не
превосходят n , имеют равные значения более чем при n различных значениях неизвестного, то f (x)= g(x).
Действительно, многочлен f (x)− g(x) имеет при наших предположениях
более чем n корней, а так как его степень не превосходит n , то должно иметь место равенство f (x)− g(x)= 0 .
Таким образом, учитывая, что различных чисел бесконечно много, можно утверждать, что для любых двух различных многочленов f (x) и g(x) найдутся
такие значения с неизвестного х, что f (c)≠ g(c). Такие с можно найти не только
среди комплексных чисел, но и среди действительных, среди рациональных и даже среди целых чисел.
3.7 Формулы Вьета
Пусть дан многочлен f (x) степени n со старшим коэффициентом 1,
|
f |
(x)= xn + a xn−1 |
+ a |
2 |
xn−2 +… + a |
n−1 |
x + a |
n |
, |
(3.18) |
|
1 |
f (x) обладает следующим |
||||||||
|
и пусть |
α1 , α2 , …, |
αn |
1) |
.PT |
Тогда |
||||
|
— его корниTP |
разложением:
f (x)= (x −α1 )(x −α2 )…(x −αn ).
Перемножая скобки, стоящие справа, а затем приводя подобные члены и сравнивая полученные коэффициенты с коэффициентами из (3.18), мы получим следующие равенства, называемые формулами Вьета и выражающие коэффициенты многочлена через его корни:
a1 = −(α1 +α2 + … +αn ),
a2 =α1α2 +α1α3 + … +α1αn +α2α3 + … +αn −1αn ,
a3 = −(α1α2α3 +α1α2α4 + … +αn−2αn −1αn ),
…………………………………………….
an −1 =( −1)n−1(α1α2 …αn −1 + α1α2 …αn −2αn + … + α2α3 …αn ), an = (−1)nα1α2…αn .
Таким образом, в правой части k -гo равенства, k =1, 2, …, n , стоит сумма
всевозможных произведений по k корней, взятая со знаком плюс или минус, в зависимости от четности или нечетности k .
При n = 2 эти формулы превращаются в известную из элементарной
|
алгебры связь между корнями и коэффициентами квадратного многочлена. При |
||
|
n = 3 , т. е. для кубичного многочлена, эти формулы принимают вид |
||
|
a1 = −(α1 +α2 +α3 ), |
a2 =α1α2 +α1α3 +α2α3 , |
a3 = −α1α2α3 . |
|
Формулы Вьета облегчают написание многочлена по заданным его |
||
|
корням. Например, найдем |
многочлен f (x) четвертой степени, имеющий |
простыми корнями числа 5 и − 2 и двукратным корнем число 3. Мы получим:
1)PT TP Каждый кратный корень взят здесь соответствующее число раз.
60

a1 = −(5 − 2 + 3 + 3)= −9 ,
a2 = 5 (− 2)+ 5 3 + 5 3 + (− 2) 3 + (− 2) 3 + 3 3 =17 ,
a3 = −[5 (− 2) 3 + 5 (− 2) 3 + 5 3 3 + (− 2) 3 3]= 33 , a4 = 5 (− 2) 3 3 = −90 ,
а поэтому
f (x)= x4 − 9x3 +17x2 + 33x − 90 .
Если старший коэффициент a0 многочлена f (x) отличен от 1, то для
применения формул Вьета необходимо сначала разделить все коэффициенты на a0 , что не влияет на корни многочлена. Таким образом, в этом случае формулы
Вьета дают выражение для отношений всех коэффициентов к старшему.
3.8 Многочлены с действительными коэффициентами. Разложение многочлена на множители
Пусть многочлен с действительными коэффициентами f (x)= xn + a1xn−1 + a2 xn−2 +… + an−1x + an
имеет комплексный корень α , т. е.
a0αn + a1αn−1 +… + an−1α + an = 0 .
Последнее равенство не нарушится, если в нем все числа заменить на сопряженные. Однако все коэффициенты a0 , a1 , …, an −1 , an , a также число 0,
стоящее справа, будучи действительными, останутся при этой замене без изменения. Следовательно, справедливо равенство
a0 αn + a1αn−1 + … + an−1α + an = 0 , т.е. f (α)= 0 .
Таким образом, если комплексное (но не действительное) число α служит корнем многочлена f (x) с действительными коэффициентами, то корнем для
f (x) будет и сопряженное число α .
Многочлен f (x) будет делиться, следовательно, на квадратный трехчлен
|
ϕ(x)= (x −α)(x − |
)= x2 − (α + |
)x +αα |
, |
(3.19) |
||
|
α |
α |
коэффициенты которого действительны. Пользуясь этим, докажем, что корни α и
α имеют в многочлене f (x) одну и ту же кратность.
Пусть, в самом деле, эти корни имеют соответственно кратности k и l и пусть, например, k > l . Тогда f (x) делится на l -ю степень многочлена ϕ(x),
f (x)=ϕl (x)q(x).
Многочлен q(x), как частное двух многочленов с действительными
коэффициентами, также имеет действительные коэффициенты, но, в противоречие с доказанным выше, он имеет число α своим (k − l) кратным
корнем, тогда как число α не является для него корнем. Отсюда следует, что k = l .
Таким образом, теперь можно сказать, что комплексные корни всякого многочлена с действительными коэффициентами попарно сопряжены. Отсюда и
61
из доказанной выше единственности разложений вида (3.14) вытекает справедливость следующей теоремы.
Теорема 3.4 Всякий многочлен f (x) с действительными коэффициентами
представим, притом единственным способом (с точностью до порядка множителей), в виде произведения своего старшего коэффициента a0 и
нескольких многочленов с действительными коэффициентами, линейных вида x −α , соответствующих его действительным корням, и квадратных вида (3.19), соответствующих парам сопряженных комплексных корней.
Для дальнейшего полезно подчеркнуть, что среди многочленов с действительными коэффициентами и со старшим коэффициентом 1, неразложимыми на множители меньшей степени или, как мы будем говорить, неприводимыми, являются лишь линейные многочлены вида x −α и квадратные многочлены вида (3.19).
3.9 Наибольший общий делитель многочленов. Алгоритм Евклида
Многочлен ϕ(x) называется общим делителем для заданных многочленов f (x) и g(x) , если он является делителем для каждого из этих многочленов.
Согласно пятому свойству делимости многочленов можно заключить, что к числу общих делителей многочленов f (x) и g(x) принадлежат все многочлены
нулевой степени (т.е. числа).
Два многочлена f (x) и g(x) называются взаимно простыми, если они не
имеют никаких общих делителей кроме многочленов нулевой степени.
Наибольшим общим делителем (коротко НОД) отличных от нуля многочленов f (x) и g(x) называется такой многочлен d (x) , который является их
общим делителем и, вместе с тем, сам делится на любой другой общий делитель этих многочленов.
Обозначение: (f (x), g(x)) — наибольший общий делитель многочленов f (x) и g(x) .
Для отыскания НОД удобно пользоваться алгоритмом Евклида (или
алгоритмом последовательного деления).
Алгоритм Евклида
Суть алгоритма Евклида, с помощью которого находится наибольший общий делитель заданных многочленов f (x) и g(x) — (f (x), g(x)), состоит в
последовательном делении сначала многочлена f (x) на g(x) , затем многочлена g(x) на полученный от первого деления остаток r1(x) , затем r1(x) на полученный от второго деления остаток r2 (x) и т.д. Поскольку степени
остатков все время понижаются, то эта цепочка последовательных делений остановится в тот момент, когда деление совершится нацело. Тот остаток rk (x) , на который нацело разделится предыдущий rk −1(x) , и будет
62
|
наибольшим общим делителем многочленов |
f (x) и g(x) . |
||||||
|
Запишем алгоритм Евклида следующей цепочкой неравенств: |
|||||||
|
f (x) = g(x)q1(x) + r1(x), |
|||||||
|
g(x) = r1(x)q2 (x) + r2 (x), |
|||||||
|
r1(x) = r2 (x)q3 (x) + r3 (x), |
|||||||
|
……………………………. |
(3.20) |
||||||
|
r |
(x) = r |
(x)q |
k −1 |
(x) |
+ r |
(x), |
|
|
k −3 |
k −2 |
k −1 |
|||||
|
rk −2 (x) = rk −1(x)qk (x) + rk (x), |
|||||||
|
rk −1(x) = rk (x)qk +1(x). |
|||||||
Последнее равенство показывает, что rk (x) служит делителем для rk −1(x) . Отсюда следует, что оба слагаемых правой части предпоследнего равенства делятся на rk (x) , а поэтому rk (x) будет делителем и для rk −2 (x) . Далее, таким же
|
путем, поднимаясь |
вверх, мы получим, что rk (x) является делителем и для |
|
rk −3 (x) , …, r2 (x) , |
r1(x) . Отсюда, ввиду второго равенства, будет следовать, что |
rk (x) служит делителем для g(x) , а поэтому, на основании первого равенства, — и для f (x) . Таким образом, rk (x) является общим делителем для f (x) и g(x) .
Возьмем теперь произвольный общий делитель ϕ(x) многочленов f (x) и g(x) . Так как левая часть и первое слагаемое правой части первого из равенств (3.20) делятся на ϕ(x) , то r1(x) также будет делиться на ϕ(x) . Переходя ко второму и следующему равенствам, мы таким же способом получим, что на ϕ(x)
|
делятся |
многочлены r2 ( x ), r3( x ), …. Наконец, если уже будет доказано, что |
|
rk −2 (x) |
и rk −1(x) делятся на ϕ(x) , то из предпоследнего равенства мы получим, |
что rk (x) делится на ϕ(x) . Таким образом, rk ( x ) на самом деле будет наибольшим общим делителем для f (x) и g(x) .
Из доказательства справедливости алгоритма Евклида следует и справедливость следующих утверждений:
1 Любые два многочлена обладают наибольшим общим делителем.
2Если многочлены f (x) и g(x) имеют оба рациональные или действительные коэффициенты, то и коэффициенты их наибольшего общего делителя также будут рациональными или, соответственно, действительными.
3Наибольший общий делитель двух многочленов определен лишь с точностью до множителя нулевой степени, т.е. если d (x) есть (f (x), g(x)), то и
многочлен cd(x) также является (f (x), g(x)) в связи с третьим утверждением.
Условимся, что старший коэффициент наибольшего общего делителя двух многочленов будет всегда считаться равным единице, а значит два многочлена тогда и только тогда взаимно просты, если их наибольший общий делитель равен единице.
63
|
НапримерU |
,U |
найдем |
наибольший |
общий |
делитель |
многочленов |
|||||
|
f (x) = x3 − 4x2 + 4x −1 и |
g(x) = x2 + 2x − 3 . |
Следуем |
строго |
по алгоритму |
|||||||
|
Евклида |
|||||||||||
|
1) f (x) : g(x) |
|||||||||||
|
− |
x3 − 4x2 + 4x −1 |
x2 + 2x − 3 |
|||||||||
|
x3 + 2x2 − 3x |
|||||||||||
|
x − 6 |
|||||||||||
|
− 6x2 + 7x −1 |
|||||||||||
|
− 6x2 −12x +18 |
|||||||||||
|
19x −19 |
Так как f (x) = g(x) q(x) + r1(x) , т.е. x3 − 4x2 + 4x −1=( x2 + 2x −3)( x −6 ) +
+(19x −19) , следовательно, r1(x) =19x −19 .
2)g(x) : r1(x)
|
_ x2 + 2x − 3 |
19x −19 |
||||||||||||
|
x2 − x |
|||||||||||||
|
1 |
x + |
3 |
|||||||||||
|
19 |
19 |
||||||||||||
|
3x − 3 |
|||||||||||||
|
3x − 3 |
|||||||||||||
|
0 |
|||||||||||||
|
т.е. получим, что |
|||||||||||||
|
1 |
3 |
||||||||||||
|
g(x) = r |
(x) |
x + |
. |
||||||||||
|
19 |
|||||||||||||
|
1 |
19 |
Следовательно, наибольшим общим делителем многочленов f (x) и g(x)
служит двучлен 19x −19 . На основании утверждения 3 наибольшим общим делителем многочлен f (x) и g(x) будем считать многочлен ( x −1).
Займемся дальнейшим исследованием делимости многочленов.
Теорема 3.5 Если d (x) есть наибольший общий делитель многочленов
|
f (x) и g(x) , то можно найти такие многочлены u(x) и v(x) , что |
|
|
f (x)u(x) + g(x)v(x) = d(x) . |
(3.21) |
Доказательство. Можно считать при этом, если степени многочленов f (x) и g(x) больше нуля, то степень u(x) меньше степени g(x) , а степень v(x)
|
меньше степени f (x) . |
||
|
Доказательство основано |
на равенствах |
(3.20). Если мы учтем, что |
|
rk (x) = d (x) , и положим u1(x) =1, |
v1(x) = −qk (x) , |
то предпоследнее из равенств |
|
(3.20) даст: |
d (x) = rk −2 (x)u1(x) + rk −1(x)v1(x) .
64
Подставляя сюда выражение rk −1(x) через rk −3 (x) и rk −2 (x) из
предшествующего равенства, мы получим: d(x) = rk −3 (x)u2 (x) + rk −2 (x)v2 (x) ,
где, очевидно, u2 (x) = v1(x) , v2 (x) = u1(x) − v1(x)qk −1(x) . Продолжая подниматься вверх по равенствам, мы придем, наконец, к доказываемому равенству.
Для доказательства второго утверждения теоремы предположим, что многочлены u(x) и v(x) , удовлетворяющие равенству (3.21), уже найдены, но,
например, степень u(x) больше или равна степени g(x) . Делим u(x) на g(x) : u(x) = g(x)q(x) + r(x) ,
где степень r(x) меньше степени g(x) , и подставляем это выражение в (3.21). Мы получим равенство f (x)(g(x)q(x)+ r(x))+ g(x)v(x)= d (x), или
f (x)r(x) + g(x)[v(x) + f (x)q(x)]= d (x) .
Степень множителя, стоящего при f (x) , уже меньше степени g(x) . Степень многочлена, стоящего в квадратных скобках, будет в свою очередь меньше степени f (x) , так как в противном случае степень второго слагаемого левой части была бы не меньше степени произведения g(x) f (x) , а так как степень первого слагаемого меньше степени этого произведения, то вся левая часть имела бы степень, большую или равную степени g(x) f (x) , тогда как многочлен d(x) заведомо имеет, при наших предположениях, меньшую степень. Теорема доказана.
Одновременно мы получаем, что если многочлены f (x) и g(x) имеют рациональные или действительные коэффициенты, то и многочлены u( x ) и v( x ), удовлетворяющие равенству (3.21) можно подобрать так, что их коэффициенты будут рациональными или, соответственно, действительными.
Представление (3.21) называется представлением d( x) (наибольшего общего делителя f (x) и g(x) ) в линейной форме.
Следствие. Многочлены f (x) и g(x) тогда и только тогда взаимно просты, если можно найти многочлены u(x) и v(x) , удовлетворяющие равенству
|
f (x)u(x) + g(x)v(x) =1. |
(3.22) |
Теоремы о взаимно простых многочленах
1 Если многочлен f (x) взаимно прост с каждым из многочленов ϕ(x) и ψ (x) , то он взаимно прост и с их произведением.
Доказательство. Поскольку по условию многочлен f (x) взаимно прост с многочленом ϕ(x) , то на основании формулы (3.22) существуют такие многочлены u(x) и v(x) , что
f (x)u(x) +ϕ(x)v(x) =1.
Умножим это равенство на ψ (x) :
f (x)[u(x)ψ (x)]+ [ϕ(x)ψ (x)]v(x) =ψ (x) ,
65

из полученного следует, что всякий общий делитель f (x) и ϕ(x) ψ (x) был бы делителем и для ψ (x) ; однако по условию (f (x),ψ (x))=1.
2 Если произведение многочленов f (x) и g(x) делится на ϕ(x) , но f (x) и ϕ(x) взаимно просты, то g(x) делится на ϕ(x) .
Доказательство. Поскольку f (x) и ϕ(x) — взаимно просты то, согласно (3.22), верно что f (x)u(x) +ϕ(x)v(x) =1. Умножим это равенство на g(x) , имеем:
[f (x)g(x)]u(x) +ϕ(x)[v(x)g(x)]= g(x) .
Так как оба слагаемых левой части этого равенства делятся на ϕ(x) , то следовательно и g(x) делится на ϕ(x) .
3 Если многочлен f (x) делится на каждый из многочленов ϕ(x) и ψ (x) , которые между собой взаимно просты, то f (x) делится и на их произведение.
Доказательство. f (x) = ϕ(x) ϕ(x) , так что произведение, стоящее справа, делится на ψ (x) . Поэтому, по второй теореме, ϕ(x) делится на ψ (x) ,
ϕ(x) =ψ (x)ψ (x) , откуда f (x) =[ϕ(x)ψ (x)]ψ (x) .
Очевидно, что определение наибольшего общего делителя может быть распространено на случай любой конечной системы многочленов.
4 Наибольший общий делитель многочленов f1(x), f2 (x), …, fs (x) равен наибольшему общему делителю многочлена fs (x) и наибольшего общего делителя многочленов f1(x), f2 (x), …, fs −1(x) .
Доказательство. При s = 2 теорема очевидна. Примем, что для случая s −1 она справедлива, т.е. уже доказано существование наибольшего общего делителя
d (x) многочленов f1(x), f2 (x), …, fs −1(x) . Обозначим через d (x) наибольший общий делитель многочленов d (x) и fs (x) . Он будет, очевидно, общим
делителем для всех заданных многочленов. С другой стороны, всякий другой общий делитель этих многочленов будет делителем также и для d (x) , а поэтому и
для d (x) .
В заключении отметим, что система многочленов f1(x), f2 (x), …, fn (x)
называется взаимно простой, если общими делителями многочленов этой системы являются только многочлены нулевой степени.
3.10 Вопросы для самоконтроля
1 Сформулируйте определение многочлена n -й степени от одной переменной.
2Какой вид многочлена называется каноническим?
3Что значит степень многочлена (нулевая степень, двучлен)?
4Какие действия возможны над многочленами?
5Свойства операций сложения и произведения многочленов.
6Сформулируйте условие существования многочлена, обратного данному.
7Что значит разделить многочлены друг на друга?
8Что значит многочлен f (x) делится нацело на многочлен ϕ(x) ?
66
9Сформулируйте и докажите теорему о делителе многочлена.
10Сформулируйте основные 9 свойств делимости многочлена.
11Какое число называется корнем многочлена?
12Сформулируйте и докажите теорему Безу.
13Чему равен остаток от деления многочлена f (x) на двучлен (x − c)?
14Чему равен остаток от деления многочлена f (x) на двучлен (ax + b)?
15Расскажите в чем заключается суть метода Горнера.
16Сформулируйте основную теорему алгебры.
17Сформулируйте и докажите следствие из основной теоремы алгебры.
18Запишите формулы, выражающие коэффициенты многочлена через его корни. Как называются эти формулы?
19Сформулируйте теорему о разложении многочлена с действительными коэффициентами на множители.
20Какие два многочлена называются взаимно простыми?
21Какой многочлен называется общим делителем заданных многочленов?
22Какой многочлен называется наибольшим общим делителем заданных многочленов?
23В чем заключается суть алгоритма Евклида?
24 Что означает представление d( x ) (наибольшего общего делителя f ( x ) и g( x )) в линейной форме.
25Сформулируйте необходимое и достаточное условие того, что многочлены f (x) и g( x ) взаимно просты.
26Докажите теорему о том, что если многочлен f (x) взаимно прост с каждым из многочленов ϕ(x) и ψ (x) , то он взаимно прост и с их произведением.
27Докажите теорему о том, что если произведение многочленов f (x) и g(x) делится на ϕ(x) , но f (x) и ϕ(x) взаимно просты, то g(x) делится на ϕ(x) .
28Докажите теорему о том, что если многочлен f (x) делится на каждый из многочленов ϕ(x) и ψ (x) , которые между собой взаимно просты, то f (x)
делится и на их произведение.
29 Докажите теорему о том, что наибольший общий делитель
|
многочленов |
f1(x), |
f2 (x), …, fs (x) равен |
наибольшему общему делителю |
|
многочлена |
fs (x) |
и наибольшего |
общего делителя многочленов |
|
f1(x), f2 (x), …, |
fs −1(x) . |
30 Какая система многочленов называется взаимно простой?
67
Соседние файлы в предмете Алгебра и начала анализа
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


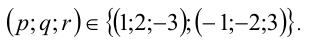
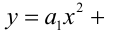
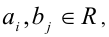
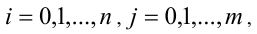
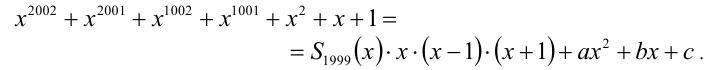
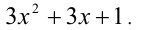
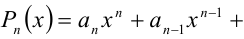
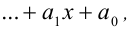
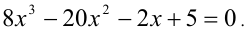
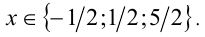
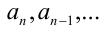
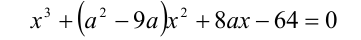
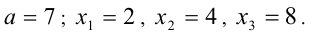







 имеет единственное решение?
имеет единственное решение?



=a_0x^{n}+a_1x^{n-1}+a_2x^{n-2}+.....+a_{n-1}x+a_n)



