Как найти путь материальной точки по графику - AutoPluse.ru

Вычисление перемещения по графику проекции скорости

Из кодификатора по физике, 2020.
«1.1.3. Вычисление перемещения по графику зависимости υ(t).»

Теория

Пусть задан график зависимости проекции скорости ${ v }_{ x }$ от времени t (рис. 1).

Проекция перемещении тела ${ s }_{ x }$ за промежуток времени от ${ t }_{ 1 }$ до ${ t }_{ 2 }$ численно равна по величине площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }$ и ${ t }_{ 2 }$ (см. рис. 1, площадь выделена штриховкой).

Проекцию перемещения на ось 0Х будем считать:

— положительной, если проекция скорости на данную ось будет положительной (тело движется по направлению оси) (см. рис. 1);

— отрицательной, если проекция скорости на данную ось будет отрицательной (тело движется против оси) (рис. 2).

Путь s может быть только положительным:

Напоминаем формулы для расчета площадей фигур:

— прямоугольника –

— треугольника – $S=frac { acdot h }{ 2 }$

— трапеции – $S=frac { a+b }{ 2 } cdot h$

Задачи

Задача 1. По графику проекции скорости тела (рис. 3) определите проекцию его перемещения между 1 и 5 с.

Ответ: ____ м.

Решение. Проекция перемещения за промежуток времени Δt= ${ t }_{ 2 }$ – ${ t }_{ 1 }$ =5с–1с=4c численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }=1$ с и ${ t }_{ 2 }=5$ с (рис. 4, площадь выделена штриховкой). Фигура ABCD — это трапеция, ее площадь равна

$S=frac { a+b }{ 2 } cdot h=frac { AD+BC }{ 2 } cdot DC$

где DC = Δt = 4 c, AD = 3 м/c, BC = 5 м/c. Тогда S = 16 м.
Проекция перемещения ${ s }_{ x }>0$ , т.к. проекция скорости ${ v }_{ x }>0$ .
${ s }_{ x }=S=16$ м.

Ответ: 16.

Задача 2. Автомобиль движется по прямой улице вдоль оси X. На рисунке 5 представлен график зависимости проекции скорости автомобиля от времени. Определите путь, пройденный автомобилем в течение указанных интервалов времени.

Интервал времени	Путь
от 0 до 10 с	Ответ: м.
от 30 до 40 с	Ответ: м.

В бланк ответов перенесите только числа, не разделяя их пробелом или другим знаком.

Решение. Путь за промежуток времени Δt = ${ t }_{ 2 }$ – ${ t }_{ 1 }$ численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t),$ осью времени 0t и перпендикулярами к ${ t }_{ 1 }$ и ${ t }_{ 2 }$ .

На интервале [0 с, 10 с] ищем площадь треугольника (рис. 6).

${ S }_{ 1 }=frac { acdot h }{ 2 }$ ,

где a = 20 м/c, $h=triangle { t }_{ 1 }=10c-0c=10c$ . Тогда ${ S }_{ 1 }=100$ м.

Путь равен значению площади (путь всегда положительный, т.е. s > 0).

${ s }_{ 1 }={ S }_{ 1 }=100$ м.

На интервале [30 с, 40 с] ищем площадь трапеции (см. рис. 6).

${ S }_{ 2 }=frac { a+b }{ 2 } cdot h$ ,

где a = 10 м/c, b = 15 м/c, h = Δt = 40 c – 30 с = 10 с. Тогда ${ s }_{ 2 }={ S }_{ 2 }=125$ м.

Ответ: 100125.

Задача 3. Определите за первые 4 с (рис. 7):

а) проекцию перемещения тела;

б) пройденный путь.

Ответ: а) ____ м; б) ____ м.

Решение. Проекция перемещения за время $triangle t={ t }_{ 2 }-{ t }_{ 1 }=4c-0=4c$ (пер-вые 4 с) численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }=0$ с и ${ t }_{ 2 }=4$ с (рис. 8, площадь выделена штриховкой).

Так как при ${ t }_{ 0 }=3$ с проекция скорости поменяла знак, то получили две фигуры, два треугольника, площади которых равны:

${ S }_{ 1 }=frac { { a }_{ 1 }cdot { h }_{ 1 } }{ 2 } ,quad { S }_{ 2 }=frac { { a }_{ 2 }cdot { h }_{ 2 } }{ 2 }$ ,

где

${ a }_{ 1 }=30quad$ м/с, $quad { h }_{ 1 }=triangle { t }_{ 1 }=3c-0c=3c$

${ a }_{ 2 }$ =|-10 м/c|=10 м/c, $quad { h }_{ 2 }=triangle { t }_{ 2 }=4c-3c=1c$ .

Тогда ${ S }_{ 1 }=45$ м, $quad { S }_{ 2 }=5$ м.

а) Проекция перемещения ${ s }_{ 1x }>0$ , т.к. проекция скорости ${ v }_{ 1x }>0$ ; проекция перемещения ${ s }_{ 2x }<0$ , т.к. проекция скорости ${ v }_{ 2x }<0$ . В итоге получаем: ${ s }_{ x }={ s }_{ 1x }+{ s }_{ 2x }={ S }_{ 1 }-{ S }_{ 2 },quad { s }_{ 1x }=$ 45м — 5м = 40 м. б) Путь равен значению площади (путь всегда положительный, т.е. s>0).

$s={ S }_{ 1 }+{ S }_{ 2 }$ , s = 45 м + 5 м = 50 м.

Ответ: а) 40; б) 50.

Задача 4. График зависимости проекции скорости материальной точки, движущейся вдоль оси 0Х, от времени изображен на рисунке 9. Определите перемещение точки, которое она совершила за первые 6 с.

Ответ: ____ м.

Решение. Проекция перемещения за время $triangle t={ t }_{ 2 }-{ t }_{ 1 }=6c-0=6c$ (пер-вые 6 с) численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }=0 c$ и ${ t }_{ 2 }=6 c$ (рис. 10, площадь выделена штриховкой).

Так как при ${ t }_{ 01 }=2c$ и ${ t }_{ 02 }=4c$ проекция скорости меняет знак, то получили три фигуры, три треугольника, площади которых равны:

${ S }_{ 1 }=frac { { a }_{ 1 }cdot { h }_{ 1 } }{ 2 } ,quad { S }_{ 2 }=frac { { a }_{ 2 }cdot { h }_{ 2 } }{ 2 } ,quad { S }_{ 3 }=frac { { a }_{ 3 }cdot { h }_{ 3 } }{ 2 } ,$

где

${ a }_{ 1 }=3$ м/с, $h_{ 1 }=triangle { t }_{ 1 }=2c-0c=2c$

${ a }_{ 2 }=$ |-2 м/c| = 2 м/с, $h_{ 2 }=triangle { t }_{ 2 }=4c-2c=2c$

${ a }_{ 2 }=$ 3м/c, $h_{ 3 }=triangle { t }_{ 3 }=6c-4c=2c$ .

Тогда ${ S }_{ 1 }=3$ м, ${ S }_{ 2 }=2$ м, ${ S }_{ 3 }=3$ м.

Проекция перемещения ${ s }_{ 1x }>0$ , т.к. проекция скорости ${ v }_{ 1x }>0$ .

Проекция перемещения ${ s }_{ 2x }<0$ , т.к. проекция скорости ${ v }_{ 2x }<0$ . Проекция перемещения ${ s }_{ 3x }>0$ , т.к. проекция скорости ${ v }_{ 3x }>0$ . В итоге получаем:

${ s }_{ x }={ s }_{ 1x }+{ s }_{ 2x }+{ s }_{ 3x }={ S }_{ 1 }-{ S }_{ 2 }+{ S }_{ 3 },quad { s }_{ x }=$ 3 м – 2 м + 3 м = 4 м.

Ответ: 4.

Задача 5. На рисунке приведен график зависимости v_x скорости тела от времени .

Определите путь, пройденный телом в интервале времени от 0 до 5 с.

Ответ: ____ м.

Решение. Решение любых графических задач основывается на умении «читать» графики. В данной задаче рассматривается зависимость проекции скорости тела от времени. На интервале от 0 до 3с проекция скорости уменьшается от значения 15 м/с до 0. На интервале от 3 до 5с модуль проекции начинает возрастать от нулевого значения до 10 м/с. Причем важно «увидеть», что тело в этом временном интервале начинает движение в направлении, противоположном оси ОХ.

Пройденный путь будет определяться площадью геометрической фигуры, образованной под графиком проекции скорости.

Рис.1

Дальнейшее решение задачи сводится к нахождению площадей двух треугольников, заштрихованных на рис.1

$S_1=frac{15cdot 3}{2}=22,5$ (м).

$S_2=frac{10cdot 2}{2}=10$ (м).

Тогда, общий путь в интервале времени от 0 до 5с будет определяться суммой отдельных путей S_1 и S_2 .

(м).
Ответ: 32,5 м

По условию этой задачи можно поставить второй вопрос: найти проекцию перемещения в интервале времени от 0 до 5с.

В этом случае надо учесть, что проекция перемещения в интервале времени от 0 до 3 с положительная и её значение равно пройденному пути на этом интервале.

$S_{1x}=S_1=22,5$ (м).

В интервале времени от 3 с до 5 с проекция перемещения отрицательная, так как тело движется в направлении противоположном оси ОХ.

$S_{2x}=-10$ (м).

Проекция перемещения за весь интервал времени будет равна $S_{o.x}=S_{1x}+S_{2x}$
$S_{o.x}=22,5+(-10)=12,5$ (м).

Ответ: 12,5 м

Задача 6. На рисунке представлен график зависимости модуля скорости v прямолинейно движущегося тела от времени t. Определите по графику путь, пройденный телом в интервале времени от 1 до 5 с.

Ответ: ____ м.

Решение. Для нахождения пройденного пути в интервале времени от 1с до 5с необходимо рассчитать площадь геометрической фигуры под графиком модуля скорости.

Рис.1

Дальнейшее решение сводится к расчету площади трапеции, заштрихованной на графике (см. рис.1).

$S=frac{4+2}{2}cdot 10=30$ (м).

Особенностью подобной задачи является то, что при решении, необходимо внимательно отследить временной интервал, на котором требуется рассчитать пройденный путь.
Ответ: 30 м.

Задача 7. Из двух городов навстречу друг другу с постоянной скоростью двиижутся два автомобиля. На графике показана зависимость расстояния между автомобилями от времени. Скорость первого автомобиля равна 15 м/с. Какова скорость второго автомобиля?

Ответ: ____ м.

Решение. При движении навстречу друг к другу расстояние между двумя автомобилями уменьшается от значения 144 км до 0. На графике видно, что встреча автомобилей произошла в момент времени 60 минут, так как расстояние между автомобилями стало равным 0. Расчеты в этой задаче требуют обязательного применения системы «СИ».

144 км = 144000 м; 60 мин = 3600 с.
Используя эти данные, можно рассчитать скорость сближения автомобилей.

$v=frac{144000}{3600}=40$ м/с

Так как автомобили движутся навстречу друг другу, то отсюда скорость второго автомобиля можно выразить как

(м/с)

Ответ: 25 м/с.

Задача 8. На рисунке представлен график зависимости модуля скорости тела от времени. Найдите путь, пройденный телом за время от момента времени 0 с до момента времени 5 с. (Ответ дайте в метрах.)

Ответ: ____ м.

Решение. Для нахождения пройденного пути необходимо рассчитать площадь геометрической фигуры (трапеции) под графиком модуля скорости (см.рис.1). Это относится к интервалу времени от 0 до 3 с. От 3 с до 5 с скорость тела равна 0, следовательно, тело находилось в состоянии покоя и пройденный путь в этом интервале равен 0.

Рис.1

$S_1=frac{3+1}{2}cdot 10=20$ (м).
S_2=0
(м).

Сакович А.Л., 2020

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Вычисление перемещения по графику проекции скорости» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Путь и перемещение, теория и онлайн калькуляторы

Путь и перемещение

При своем движении материальная точка описывает некоторую линию, которую называют ее траекторией движения. Траектория может быть прямой линией, а может представлять собой кривую.

Путь

Определение

Путь — длина участка траектории, который прошла материальная точка за рассматриваемый отрезок времени. Путь — это скалярная величина.

При прямолинейном движении в одном направлении пройденный путь ($Delta s$) равен модулю изменения координаты тела. Так, если тело двигалось по оси X, то путь можно найти как:

[Delta s=left|x_2-x_1right|left(1right),]

где $x_1$ — координата начального положения тела; $x_2$ — конечная координата тела.

Его можно вычислить, если известен модуль скорости ($v=v_x$):

[Delta s=vt left(2right),]

где $t$ — время движения тела.

Графиком, который отображает зависимость пути от времени при равномерном прямолинейном движении, является прямая (рис.1). С увеличением величины скорости увеличивается угол наклона прямой относительно оси времени.

Если по графику $Delta s(t)$ необходимо найти путь, который проделало тело за время $t_1$, то из точки $t_1$ на оси времени проводят перпендикуляр до пересечения с графиком $Delta s(t)$. Затем из точки пересечения восстанавливают перпендикуляр к оси $Delta s$. На пересечении оси и перпендикуляра получают точку ${Delta s}_1$, которая соответствует пройденному пути за время от $t=0 c$ до $t_1$.

Путь не бывает меньше нуля и не может уменьшаться при движении тела.

Перемещение

Определение

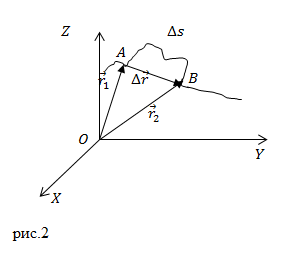
Перемещением называют вектор, который проводят из начального положения движущейся материальной точки в ее конечное положение:

[Delta overline{r}=overline{r }left(t+Delta tright)-overline{r }left(tright)left(3right).]

Вектор перемещения численно равен расстоянию между конечной и начальной точками и направлен от начальной точки к конечной.

Приращение радиус-вектора материальной точки — это перемещение ($Delta overline{r}$).

В декартовой системе координат радиус-вектор точки представляют в виде:

[overline{r }left(tright)=xleft(tright)overline{i}+yleft(tright)overline{j}+zleft(tright)overline{k}left(4right),]

где $overline{i}$, $overline{j}$,$ overline{k}$ — единичные орты осей X,Y,Z. Тогда $Delta overline{r}$ равен:

[Delta overline{r}=left[xleft(t+Delta tright)-xleft(tright)right]overline{i}+left[yleft(t+?tright)-yleft(tright)right]overline{j}+left[zleft(t+?tright)-zleft(tright)right]overline{k}left(5right).]

При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина вектора перемещения равна пройденному точкой пути:

[left|Delta overline{r}right|=Delta s left(6right).]

Длину вектора перемещения (как и любого вектора) можно обозначать как $left|Delta overline{r}right|$ или просто $Delta r$ (без указания стрелки).

Если тело совершает несколько перемещений, то их можно складывать по правилам сложения векторов:

[Delta overline{r}=Delta {overline{r}}_1+Delta {overline{r}}_2+dots left(7right).]

Если направление движения тела изменяется, то модуль вектора перемещения не равен пройденному телом пути.

Примеры задач на путь и перемещение

Пример 1

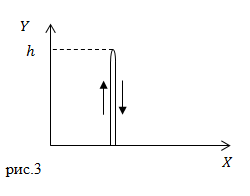
Задание: Мяч бросили вертикально вверх от поверхности Земли. Он долетел до высоты 20 м. и упал на Землю. Чему равен путь, который прошел мяч, каков модуль перемещения?

Решение: Сделаем рисунок.

В нашей задаче мяч движется прямолинейно сначала вверх, затем вниз. Так как путь — длина траектории, то получается, что мяч дважды прошел расстояние h, следовательно:

[Delta s=2h.]

Перемещение — направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю:

[Delta r=0.]

Ответ: $ Путь Delta s=2h$. Перемещение $Delta r=0$

Пример 2

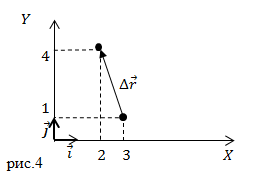
Задание: В начальный момент времени тело находилось в точке с координатами $(x_0=3;; y_0=1)$(см). Через некоторый промежуток времени оно переместилось в точку координаты которой ($x=2;;y=4$) (см). Каковы проекции вектора перемещения на оси X и Y?

Решение: Сделаем рисунок.

Радиус — вектор начальной точки запишем как:

[{overline{r }}_0left(tright)=x_0left(tright)overline{i}+y_0left(tright)overline{j}=3overline{i}+1overline{j}left(2.1right).]

Радиус — вектор конечной точки имеет вид:

[overline{r}left(tright)=xleft(tright)overline{i}+yleft(tright)overline{j}=2overline{i}+4overline{j}left(2.2right).]

Вектор перемещения представим как:

[Delta overline{r}=left[xleft(tright)-x_0left(tright)right]overline{i}+left[уleft(tright)-у_0left(tright)right]overline{j}=left[2-3right]+left[1-4right]overline{j}=-1overline{i}+3overline{j}(2.3).]

Из формулы видим, что:

[Delta r_x=-1;;Delta r_y=3. ]

Ответ: $Delta r_x=-1;;Delta r_y=3 $

Читать дальше: равнодействующая всех сил.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

По графику скорости от времени v(t) можно найти перемещение тела. Для этого нужно уметь рассчитывать площади плоских фигур.

По-английски «Square» – значит «площадь». Первая буква этого слова – буква «S». Перемещение обозначают буквой S потому, что S – это площадь фигуры, заключенной между линией скорости и горизонтальной осью времени.

Как вычислить площади плоских фигур

Рис.1. Чтобы рассчитать перемещение по графику v(t) нужно уметь вычислять площади трех плоских фигур

Площадь прямоугольника

Площадь прямоугольника (рис. 1а) можно найти, перемножив две его перпендикулярные стороны:

[ large boxed{ S_{text{прямоуг}} = a cdot b }]

Площадь трапеции

Примечание: Трапеция – это четырехугольник, две его стороны параллельные, а две другие – не параллельные. Параллельные стороны называются основаниями трапеции.

Умножив полусумму оснований трапеции на ее высоту, получим площадь (рис. 1б) трапеции:

[ large boxed{ S_{text{трапец}} = frac{1}{2} (a + b) cdot h }]

Площадь прямоугольного треугольника

Для прямоугольного треугольника (рис. 1в) площадь можно вычислить, перемножив два его катета и взяв половину от получившегося произведения:

[ large boxed{ S_{text{треуг}} = frac{1}{2} cdot a cdot b }]

Скорость не меняется

Пусть тело движется по прямой и при этом его скорость не изменяется (остается одной и той же). На языке математики «скорость не изменяется» можно записать так:

[v=const]

На графике для скорости v(t) такая скорость обозначается горизонтальной линией. На рисунке 2 эта линия обозначена синим цветом.

Рис.2. Площадь прямоугольника на графике v(t), если скорость тела не изменяется, будет численно равна перемещению тела

Примечание: Движение с постоянной (т. е. с одной и той же) скоростью называют равномерным движением.

Если скорость направлена по оси движения – линия лежит выше оси t времени (рис. 2а).

А когда скорость направлена против оси движения – линия скорости располагается ниже оси t времени (рис. 2б). Математики в таком случае говорят: «Скорость имеет отрицательную проекцию на ось».

Какую бы проекцию не имела скорость – положительную, или отрицательную, длина вектора скорости остается положительной. Поэтому, когда мы вычисляем площадь фигуры, то не учитываем знак «минус» для скорости (рис. 2б).

В обоих случаях перемещение тела можно вычислить по формуле:

[ large S = v_{0} cdot (t_{2} — t_{1}) ]

Примечание: Перемещение тела – это всегда либо нулевая, либо положительная величина S. Математики словосочетание «либо нулевая, либо положительная» заменят одним словом «не отрицательная».

Скорость увеличивается

Когда скорость тела увеличивается, то линия скорости на графике v(t) всегда располагается так, чтобы с ростом времени удаляться от оси времени. Чем больше времени пройдет, тем дальше от горизонтали располагаются точки, лежащие на линии скорости (рис. 3).

Рис.3. Так выглядит зависимость скорости от времени v(t), когда тело увеличивает свою скорость, двигаясь по оси – рис а) и против оси – рис. б)

Примечание: Движение с возрастающей скоростью называют равноускоренным движением.

Когда тело движется по направлению оси, линия скорости расположена выше горизонтальной оси времени (рис 3а).

А если тело движется против оси, линия скорости располагается ниже горизонтальной оси времени (рис. 3б).

Вычислим перемещение тела, движущегося в положительном направлении оси Ox. Для тела, движущегося противоположно оси, перемещение рассчитывается аналогично.

Выбор интервала времени влияет на то, будем ли мы вычислять площадь трапеции (рис. 4а), или прямоугольного треугольника (рис. 4б).

Рис.4. График v(t) — тело движется в положительном направлении оси и увеличивает свою скорость. От того, какой интервал времени мы выберем, зависит, будем ли мы вычислять путь, пройденный телом, с помощью площади трапеции – рис. а), или прямоугольного треугольника — рис. б)

На графике скорости v(t) для рисунка 4а перемещение с помощью трапеции вычисляется так:

[ large S = frac{1}{2} cdot (v_{1} + v_{2}) cdot (t_{2} — t_{1}) ]

А для рисунка 4б перемещение тела найдем с помощью площади треугольника:

[ large S = frac{1}{2} cdot v_{2} cdot (t_{2} — 0) ]

Скорость уменьшается

Когда тело замедляется и его скорость уменьшается, с ростом времени линия скорости приближается к горизонтальной оси t

сверху – если тело движется по оси (рис. 5а),
или снизу – когда тело движется против оси (рис. 5б).

Рис.5. Так выглядит зависимость скорости от времени v(t), когда тело уменьшает свою скорость, двигаясь по оси – рис а) и против оси – рис. б)

Примечание: Движение с уменьшающейся по модулю скоростью называют равнозамедленным движением.

Будем вычислять перемещение тела, движущегося в положительном направлении оси Ox. Аналогичным способом рассчитывается перемещение тела, движущегося противоположно оси.

От того, какой интервал времени нас интересует, зависит, будем ли мы вычислять площадь трапеции (рис. 6а), или треугольника (рис. 6б).

Рис.6. График v(t) — тело движется в положительном направлении оси и уменьшает свою скорость. Выбор интервала времени определяет, будем ли мы вычислять путь, пройденный телом, с помощью трапеции – рис. а), или треугольника — рис. б)

Найдем на графике v(t) перемещение с помощью площади трапеции для рисунка 6а:

[ large S = frac{1}{2} cdot (v_{1} + v_{2}) cdot (t_{2} — t_{1}) ]

А для рисунка 6б перемещение тела найдем с помощью площади треугольника:

[ large S = frac{1}{2} cdot v_{1} cdot (t_{2} — t_{1}) ]

Выводы

На графике v(t) перемещение – это:

площадь прямоугольника, когда скорость не изменяется;
площадь треугольника, или трапеции, когда скорость изменяется — падает, или растет.

Источник

Рассмотрим некоторые особенности перемещения тела при прямолинейном равноускоренном движении без начальной скорости. Уравнение, которое описывает это движение, было выведено Галилеем в (XVI) веке. Необходимо помнить, что при прямолинейном равномерном или неравномерном движении модуль перемещения совпадает по своему значению с пройденным путём. Формула выглядит следующим образом:

s=v0t+at22

, где (а) — это ускорение.

Сравним графики равномерного и равноускоренного движения.

Графики прямолинейного равномерного движения

Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость (a(t)) — прямая линия, которая лежит на оси времени.

Зависимость скорости от времени. Скорость со временем не изменяется, график (v(t)) — прямая линия, параллельная оси времени.

Правило определения пути по графику (v(t)): численное значение перемещения (пути) — это площадь прямоугольника под графиком скорости.

Зависимость пути от времени. График (s(t)) — наклонная линия.

Рис. (1). График зависимости скорости от времени при равномерном прямолинейном движении

Рис. (2). График зависимости пути от времени при равномерном прямолинейном движении

Графики равноускоренного движения

Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график (a(t)) — прямая линия, параллельная оси времени.

Зависимость скорости от времени. Скорость изменяется согласно линейной зависимости.

Зависимость пути от времени. При равноускоренном движении путь изменяется согласно квадратной зависимости:

s=v0t+at22

. В координатах зависимость имеет вид:

x=x0+v0xt+axt22

Графиком является ветка параболы.

Рис. (3). График зависимости пути от времени при равноускоренном движении

Источники:

Рис. 1. График зависимости скорости от времени при равномерном прямолинейном движении. © ЯКласс.
Рис. 2. График зависимости пути от времени при равномерном прямолинейном движении. © ЯКласс.

Источник

Физика

Тема 2: Кинематика

Урок 8: Графический способ нахождения пути и перемещения

Видео
Тренажер
Теория

Заметили ошибку?

Графический способ нахождения пути и перемещения

При равномерном движении, проекция перемещения на ось х (S_x) вычисляется как S _x=v _x t.

Если мы на графике изобразим зависимость скорости v xот времени, то получим прямую линию, параллельную оси t . Тогда S xна графике – это площадь прямоугольника

Если тело движется против оси х, то проекция скорости vнаправлена против оси х и v x будет отрицательной. Тогда

S_x=−v_x t.

При неравномерном движении, мы разбиваем проекцию перемещения на маленькие участки, где на каждом участке, скорость практически не менялась и движение равномерно

Сложив площади всех маленьких участков (где площадь каждого участка S _x=v _x t ¿, мы получим общую площадь под графиком, т. е. проекцию перемещения на ось t .

Задача 1

Электропоезд, отходящий от станции, в течение 0,5 мин двигался с ускорением 0,8 м/с2. Определите путь, который он прошёл за это время, и скорость в конце пути.

Дано

Решение

Задача 2

Тело движется прямолинейно вдоль оси ОХ (рис 8). График зависимости скорости V x от времени представлен на рисунке 7. По данному графику определите перемещение и путь, пройденные телом за время t = 6 с.

Заметили ошибку?

Расскажите нам об ошибке, и мы ее исправим.

Источник

Вычисление перемещения по графику проекции скорости

Теория

Задачи

Путь и перемещение

Путь

Перемещение

Примеры задач на путь и перемещение

Как вычислить площади плоских фигур

Площадь прямоугольника

Площадь трапеции

Площадь прямоугольного треугольника

Скорость не меняется

Скорость увеличивается

Скорость уменьшается

Выводы

Физика

Урок 8: Графический способ нахождения пути и перемещения

Заметили ошибку?

Не пропустите также: