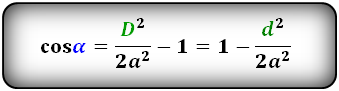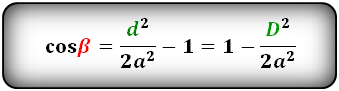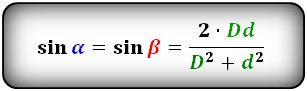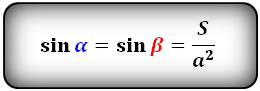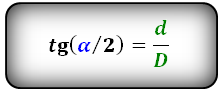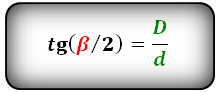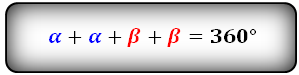Свойства ромба:
1. Ромб — частный случай параллелограмма
2. Противоположные стороны — параллельны
3. Все четыре стороны — равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами
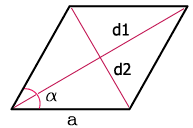
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы косинуса углов через диагональ и сторону:
Формулы синуса углов через диагонали :
Формулы синуса углов через площадь S и сторону :
Формулы тангенса половинных углов через диагонали
Формулы соотношения острого и тупого углов:
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin или arctg
Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
- Подробности
-
Опубликовано: 25 ноября 2011
-
Обновлено: 13 августа 2021
Найти углы ромба, зная только его сторону, нельзя: существуют ромбы, имеющие разные углы, но одинаковые стороны. На пальцах: сделайте ромб из проволоки, «сплющите» его — он останется ромбом, стороны будут те же, углы изменятся.
Значит, чтобы найти углы ромба нужно знать что-то ещё (или что-то другое). Например, зная сторону и диагональ, найти угол можно по теореме косинусов: если x — сторона, d — диагональ, a — угол напротив диагонали, то условие теоремы косинуов — d^2 = x^2 + x^2 — 2 * x^2 * cos(a), из него следует a = arccos((2x^2 — d^2)/2x^2). (Я говорю «найти угол», а не «найти углы», потому что если мы знаем один угол, остальные находятся тривиально: если один угол равен а градусов, то угол напротив него тоже а, остальные два — по 180-а).
Есть и другие варианты: через сторону и площадь (пользуясь тем, что площадь — это квадрат стороны умножить на синус угла), через две диагонали (мы знаем, что диагонали в ромбе пересекаются под прямым углом и делятся точкой пересечения пополам — отсюда следует, что тангенс половины угла ромба равен отношению диагоналей, просто по определнию тангенса; зная сторону и диагональ, кстати, тоже можно искать угол примерно таким способом, вместо теоремы косинусов) и так далее.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Смотрите также



Найти углы ромба зная диагональ и длину стороны
Введите сторону ромба (a) и диагональ (d).
Формула расчёта углов ромба зная диагональ и длину стороны:
cos(α)=d2/(2*a2), β=(360-α*2)/2.
Косинус α равен, диагональ в квадрате разделённое на сторону, в квадрате, умноженное на два. Угол β — вычитаем из 360 градусов угол α умноженный на два, всё это делим на два.
| Диагональ ромба (d) | ||
| Сторона ромба (a) |
Площадь ромба
Периметр ромба
Длина сторон ромба через диагонали
Найти высоту ромба через сторону и угол
Найти диагонали ромба зная длину стороны и угол
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
Оставить комментарий
Заполните все поля.
Ваше имя:
| Оценка |
Углы ромба
Угол
Ромб — вид параллелограмма, у которого все стороны одинаковые. Соответственно, периметр ромба будет равен его стороне, умноженной на четыре. Противоположные стороны ромба, как и в параллелограмме, параллельны друг другу. Противолежащие углы ромба равны, при этом, одна пара углов — острые, вторая пара — тупые. Два угла, прилегающие к одной стороне ромба (острый и тупой), составляют развернутый угол равный 180°. Если две противоположные вершины соединить отрезком, то получим диагональ ромба. Диагонали ромба взаимно перпендикулярны, в точке пересечения делятся пополам, а также делят ромб на 4 одинаковых прямоугольных треугольника. Гипотенузой в таком треугольнике является сторона ромба, катетами — половины диагоналей, а острый угол составляет половину угла ромба.
Если известна диагональ и сторона ромба, можно вычислить угол ромба с помощью теоремы косинусов.
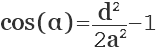
где d — диагональ, а — сторона ромба.
Т.е. косинус угла (α) равен квадрату диагонали (d) деленной на 2 квадрата стороны ромба (а) и минус единица.
В тригометрической таблице находим угол, соответствующий полученному значению косинуса. Другой, смежный с ним угол ромба, определим путем вычитания из 180° величины найденного угла. Итак, нам известны два смежных угла ромба (острый и тупой), соответственно, мы нашли все его углы, т.к. в ромбе противоположные углы равны.