Как найти угол правильной четырехугольной призмы

Правильная четырехугольная призма

Определение.

Правильная четырехугольная призма — это шестигранник, основаниями которого являются два равных квадрата, а боковые грани представляют собой равные прямоугольники

Боковое ребро — это общая сторона двух смежных боковых граней

Высота призмы — это отрезок, перпендикулярный основаниям призмы

Диагональ призмы — отрезок, соединяющий две вершины оснований, которые не принадлежат к одной грани

Диагональная плоскость — плоскость, которая проходит через диагональ призмы и ее боковые ребра

Диагональное сечение — границы пересечения призмы и диагональной плоскости. Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник

Перпендикулярное сечение (ортогональное сечение) — это пересечение призмы и плоскости, проведенной перпендикулярно ее боковым ребрам

Элементы правильной четырехугольной призмы

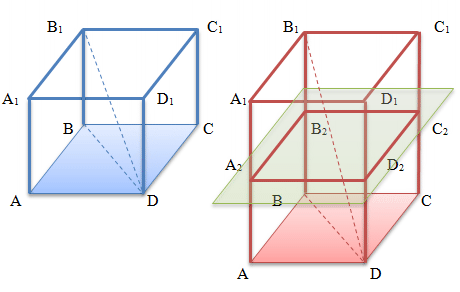
На рисунке изображены две правильные четырехугольные призмы, у которых обозначены соответствующими буквами:

Основания ABCD и A₁B₁C₁D₁ равны и параллельны друг другу
Боковые грани AA₁D₁D, AA₁B₁B, BB₁C₁C и CC₁D₁D, каждая из которых является прямоугольником
Боковая поверхность — сумма площадей всех боковых граней призмы
Полная поверхность — сумма площадей всех оснований и боковых граней (сумма площади боковой поверхности и оснований)
Боковые ребра AA₁, BB₁, CC₁ и DD₁.
Диагональ B₁D
Диагональ основания BD
Диагональное сечение BB₁D₁D
Перпендикулярное сечение A₂B₂C₂D₂ .

Свойства правильной четырехугольной призмы

Основаниями являются два равных квадрата
Основания параллельны друг другу
Боковыми гранями являются прямоугольники
Боковые грани равны между собой
Боковые грани перпендикулярны основаниям
Боковые ребра параллельны между собой и равны
Перпендикулярное сечение перпендикулярно всем боковым ребрам и параллельно основаниям
Углы перпендикулярного сечения — прямые
Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник
Перпендикулярное (ортогональное сечение) параллельно основаниям

Формулы для правильной четырехугольной призмы

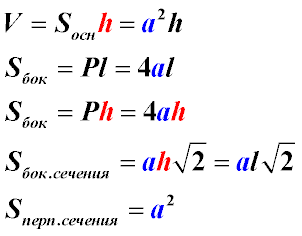
Указания к решению задач

При решении задач на тему «правильная четырехугольная призма» подразумевается, что:

Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания. То есть правильная четырехугольная призма содержит в своем основании квадрат. (см. выше свойства правильной четырехугольной призмы)

Примечание. Это часть урока с задачами по геометрии (раздел стереометрия — призма). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ .

Задача.

В правильной четырёхугольной призме площадь основания 144 см², а высота 14 см. Найти диагональ призмы и площадь полной поверхности.

Решение.
Правильный четырехугольник — это квадрат.
Соответственно, сторона основания будет равна

√144 = 12 см.
Откуда диагональ основания правильной прямоугольной призмы будет равна
√( 12² + 12² ) = √288 = 12√2

Диагональ правильной призмы образует с диагональю основания и высотой призмы прямоугольный треугольник. Соответственно, по теореме Пифагора диагональ заданной правильной четырехугольной призмы будет равна:
√( ( 12√2 )² + 14² ) = 22 см

Ответ: 22 см

Задача

Определите полную поверхность правильной четырехугольной призмы, если ее диагональ равна 5 см, а диагональ боковой грани равна 4 см.

Решение.
Поскольку в основании правильной четырехугольной призмы лежит квадрат, то сторону основания (обозначим как a) найдем по теореме Пифагора:

a² + a² = 5²
2a² = 25
a = √12,5

Высота боковой грани (обозначим как h) тогда будет равна:

h² + 12,5 = 4²
h² + 12,5 = 16
h² = 3,5
h = √3,5

Площадь полной поверхности будет равна сумме площади боковой поверхности и удвоенной площади основания

S = 2a² + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 см² .

Ответ: 25 + 10√7 ≈ 51,46 см² .

15306.1214

Прямая призма |

Описание курса

| Куб

Источник

Диагональ
правильной четырехугольной призмы
образует с плоскостью боковой грани
угол 30⁰. Найти угол между
диагональю и плоскостью основания.

Решение:

Для начала
необходимо разобраться — что такое
правильная четырехугольная призма?

Четырехугольная
призма — это призма, основаниями
которой являются четырехугольники.

Правильная призма
— это прямая призма, основаниями которой
являются правильные многоугольники.

Прямая призма —
это призма, боковые ребра которой
перпендикулярны плоскостям оснований.

Правильный
многоугольник — это многоугольник, у
которого все стороны и все внутренние
углы равны (соответственно, правильный
четырехугольник — это квадрат).

Таким образом,
правильная четырехугольная призма — это
призма, у которой в основаниях квадраты,
а боковые ребра перпендикулярны
основаниям.

Рассмотрим рисунок
такой призмы:

Рассмотрим
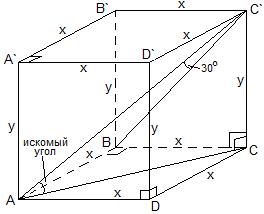
диагональ AC`.

Для того, чтобы
найти угол между прямой (например,
прямой a) и плоскостью —
необходимо из любой точки прямой a, не лежащей
на плоскости, опустить на эту плоскость
перпендикуляр. Через точку пересечения
перпендикуляра с плоскостью и точку
пересечения прямой a с плоскостью
провести прямую b. Угол между прямыми a и b
— это и есть угол между прямой a и
плоскостью.

Найдем угол между
прямой AC` и плоскостью BB`C`C.

Мы знаем, что ребро BB`^
плоскости ABCD, следовательно AB^BB`
и BC^BB`.
Поскольку в основании — квадрат, то AB^BC.
То есть все три прямые AB, BB` и BC
взаимноперпендикулярны. Следовательно
прямая AB ^
плоскости BB`C`C.

Отсюда следует, что
угол между диагональю AC` и плоскостью
BB`C`C — это угол между прямой AC` и прямой BC`.

Из точки A прямой AC`,
не принадлежащей плоскости BB`C`C,
опустили перпендикуляр на эту плоскость
(AB). Точка пересечения перпендикуляра и
плоскости — это точка B. Через точки
пересечения с плоскостью прямой AC` (т. C`)
и перпендикуляра AB (т. B) проводим прямую
BC`. Угол между прямой BC` и прямой AC` — это и
есть угол между диагональю и плоскостью
боковой грани.

Т.е. угол между
диагональю и боковой гранью BB`C`C — это
угол AC`B. По условию задачи Ð
AC`B=30⁰.

Рассуждая
аналогично, находим, что угол между
диагональю AC` и плоскостью основания ABCD —
это угол C`AC.

Пусть длины сторон
квадратов оснований равны x, а длины
боковых ребер равны y.

Из прямоугольного
треугольника BC`C находим BC`=Ö(x²+y²).
Этот треугольник прямоугольный, т.к.
ребра перпендикулярны плоскостям
оснований, а значит и любой прямой в этой
плоскости, т.е. угол BCC` — прямой.

Из прямоугольного
треугольника ABC` находим tg(Ð
AC`B)=AB/BC`, т.е.

tg30⁰=x/Ö(x²+y²).
Этот треугольник прямоугольный, т.к. AB —
перпендикуляр к плоскости BB`C`C, а значит
угол ABC` — прямой. Преобразуем полученное
выражение:

1/Ö3=x/Ö(x²+y²)

x²+y²=3x²

y²=2x²

y=xÖ2
(1)

Из прямоугольного
треугольника ACD находим AC=Ö(x²+x²)=xÖ2.

Из прямоугольного
треугольника AC`C находим tg(Ð
C`AC)=C`C/AC=y/(xÖ2)
(2)

Подставив в
выражение (2) выражение (1), получим:

tg(Ð
C`AC)=xÖ2/(xÖ2)=1

Отсюда находим,
что Ð C`AC=45⁰.

Источник

Вы здесь:

Главная
Правильная четырехугольная призма

Правильная четырехугольная призма

Четырехугольная призма — это многогранник, две грани которого являются равными квадратами, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими квадратами.

Правильная четырехугольная призма — это четырехугольная призма у которой основания квадраты, а боковые грани прямоугольники.

Данное геометрическое тело по своим свойствам и характеристикам соответствует — параллелепипеду.

Основания призмы являются равными квадратами.

Боковые грани призмы являются прямоугольниками.

Боковые рёбра призмы параллельны и равны.

Размеры призмы можно выразить через длину стороны a и высоту h.

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.

Формула площади поверхности четырехугольной призмы:

Объём призмы равен произведению её высоты на площадь основания.

Формула объема правильной четырехугольной призмы:

Правильная четырехугольная призма может быть вписана в цилиндр.

Формула радиуса цилиндра вписанной четырехугольной призмы:

Двойственным многогранником прямой призмы является бипирамида.

Исторически понятие «призма» возникло из латыни и означало — нечто отпиленное.

Анимация демонстрирует как две параллельные плоскости отрезая лишнее формируют два основания призмы. Из одной заготовки можно получить как правильную призму, так и наклонную призму.

Геометрические размеры готовой призмы (мм):

Длина = 68

Ширина = 68

Высота = 52

Геометрические размеры готовой призмы (мм):

Длина = 59

Ширина = 59

Высота = 83

Геометрические размеры готовой призмы (мм):

Длина = 43

Ширина = 43

Высота = 110

посмотреть другие призмы

В правильной четырёхугольной призме

Дата: 2021-05-05

435

Категория: Стерео Призма

Метка: ЕГЭ-№2

318475. В правильной четырёхугольной призме ABCDA₁B₁C₁D₁известно, что AC₁= 2BC. Найдите острый угол между диагоналями BD₁ и CA₁. Ответ дайте в градусах.

Построим правильную четырёхугольную призму, обозначим вершины, построим диагонали BD₁ и CA₁:

Сразу отметим, что диагонали BD₁ и CA₁ являются диагоналями прямоугольника A₁BCD₁, то есть они равны между собой и равны диагонали AC₁ (так как призма правильная четырехугольная).

Известно, что диагонали прямоугольника равны и точкой пересечения делятся пополам, то есть:В условии сказано, что AC₁ = 2BC, значит имеем BD₁= CA₁ = 2BC. На основании изложенного можем сделать вывод о том, что:то есть треугольники BОС и A₁OD₁ равносторонние. Таким образом, угол острый между диагоналями равен 60⁰.

Ответ: 60

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.

Источник

При решении задач очень важно уметь обозначать углы, образованные диагоналями призмы и её боковыми гранями.

Угол между наклонной и плоскостью — это угол между наклонной и её проекцией на эту плоскость.

Чтобы найти угол между наклонной и плоскостью, необходимо:

2. из конца наклонной провести перпендикуляр к плоскости;

3. провести проекцию наклонной;

4. обозначить угол между наклонной и её проекцией.

Углы между диагональю и плоскостью основания в прямом параллелепипеде