Ведение статистики, тестирование различных вариантов данных с отслеживанием эффективности изменений имеет огромное значение в отношении выбора той или иной концепции развития. Однако для анализа важно выбрать только значимые для статистики данные. В этой статье разберемся с понятием статистическая значимость в целом и в A/B тестах, а также рассмотрим, как ее оценивать и рассчитывать.
Что такое статистическая значимость
В процессе любого исследования стоит задача выявить связи между переменными, которые, как правило, характеризуются направлением, силой и надежностью. Чем выше вероятность повторного обнаружения связи, тем она надежнее.
Для проверки гипотез при проведении различных тестов применяется методика статистического анализа. Результатом оценки уровня надежности связи и проверки гипотезы выступает статистическая значимость (statistical significance). Чем меньше вероятность, тем надежнее будет связь.
Статистическая значимость – это параметр, который подтверждает, что результаты исследования были достигнуты не случайно.
Аналитик делает такое заключение, используя метод статистической проверки гипотез. По итогам теста определяется p-значение или значение уровня значимости. Чем оно меньше, тем больше будет статистическая значимость.
Обратите внимание! Слово «значимость» в данном контексте отличается по смыслу от общепринятого. Статистически значимые значения не обязательно являются значимыми или важными. Если же уровень значимости низкий, это не говорит о том, что итоги эксперимента не имеют ценности на практике.
Говоря о статистической значимости, стоит иметь ввиду:
- уровень значимости дает понять, что связь между переменными не случайна;
- уровень значимости в статистике может служить доказательством правдоподобности нулевой гипотезы;
- в ходе проверки получаем информацию о том, что результат эксперимента является или не является статистически значимым.
Значимость статистического критерия применяют при испытаниях вакцин, эффекта новых лекарственных препаратов, изучении болезней, а также при определении, насколько успешна и эффективна работа компании, при A/B тестировании сайтов в маркетинге, а также в различных областях науки, психологии.
История понятия уровня значимости
Статистика помогает решать задачи в различных сферах много веков, однако о статистической значимости заговорили лишь в начале XX столетия. Ввел это понятие в 1925 году британский генетик и статистик сэр Рональд Фишер, который работал над методикой проверки гипотез.
В процессе анализа любого процесса есть вероятность, что произойдут те или иные явления. Итоги эксперимента, которые имели высокую вероятность стать действительными, Фишер описывал словом «значимость» (в переводе с английского significance).
Если данные были недостаточно конкретные для проверки, возникала проблема нулевой гипотезы. Для таких систем в качестве удобной для отклонения нулевой гипотезы выборки исследователем было предложено считать вероятность событий как 5%.
Как оценить статистическую значимость
Для проверки гипотезы используют статистический анализ, при этом уровень значимости определяется с помощью p-значения. Последнее показывает вероятность события, если предположить, что определенная нулевая гипотеза верна.
Весь процесс оценивания уровня значимости можно разделить на 3 стадии, которые, в свою очередь, включают следующие промежуточные этапы.
Постановка эксперимента
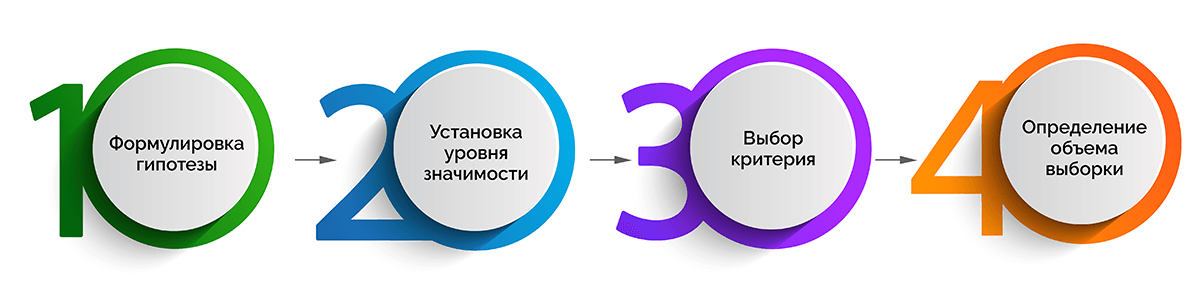
- Формулировка гипотезы.
- Установка уровня значимости, который поможет определить отклонение в распределении данных для идентификации значимого результата.
Если р-значение меньше или равно уровню значимости, данные можно считать статистически значимыми.
- Выбор критерия – одностороннего или двустороннего.
Первый подходит для случаев, когда известно, в какую сторону от нормального значения могут отклониться данные. Второй критерий лучше выбирать, если трудно понять возможное направление отклонения данных от контрольной группы значений. - Определение объема выборки с использованием статистической мощности. Она показывает вероятность того, что при заданной выборке будет получен именно ожидаемый результат. Зачастую пороговая (критическая) цифра мощности – 80%.
Вычисление стандартного отклонения

- Расчет стандартного отклонения, которое показывает величину разброса данных на заданной выборке.
- Поиск среднего значения в каждой исследуемой группе. Для этого осуществляют сложение всех значений, а сумму делят на их количество.
- Определение стандартного отклонения (xi – µ). Разница вычисляется путем вычитания каждого полученного значения из средней величины.
- Возведение полученных величин в квадрат и их суммирование. На данном этапе все числа со знаком «минус» должны исчезнуть.
- Деление суммы на общий объем выборки минус 1. Единица – это генеральная совокупность, которая не учитывается в расчете.
- Извлечение корня квадратного.
Определение значимости
- Определение дисперсии между двумя группами данных по формуле:
sd = √((s1/N1) + (s2/N2)), где:
s1 – стандартной отклонение в первой группе;
s2 – стандартное отклонение во второй группе;
N1 – объем выборки в первой группе;
N2 – объем выборки во 2-й группе. - Поиск t-оценки данных. С ее помощью можно переводить данные в такую форму, которая позволит использовать их в сравнении с другими значениями. T-оценка рассчитывается по формуле:
t = (µ1 – µ2)/sd, где:
µ1 – среднее значение для 1-й группы;
µ2 – среднее значение для 2-й группы;
sd – дисперсия между двумя группами. - Определение степени свободы выборки. Для этого объемы двух выборок складывают и вычитают 2.
- Оценка значимости. Ее осуществляют по таблице значений t-критерия (критерия Стьюдента).
- Повышение уверенности в достоверности выводов путем проведения дальнейшего исследования.
Статистическая значимость и гипотезы
Гипотеза – это теория, предположение. Если требуется проверка гипотез, всегда используется статистическая значимость. Предположение же называется гипотезой до тех пор, пока это утверждение не будет опровергнуто или доказано.

Гипотезы бывают двух типов:
- нулевая гипотеза – теория, не требующая доказательств. Согласно нее, при внесении изменений ничего не произойдет, т. е. стоит задача не доказать это, а опровергнуть;
- альтернативная гипотеза (исследовательская) – теория, в пользу которой нужно отклонить нулевую гипотезу, т. е. предстоит доказать, что одно решение лучше другого.
Рассмотрим, как статистическая значимость влияет на подтверждение или опровержение альтернативной гипотезы на простом примере.
У компании запущена реклама, которая стала давать меньше конверсий и продаж, чем месяц назад. По мнению маркетолога, причина кроется в рекламных креативах, которые приелись аудитории и требуют замены. Специалист предлагает заменить текстовый материал объявления. Гипотеза состоит в том, что после внесенных изменений будет достигнута главная цель эксперимента: клиенты, пришедшие на сайт с рекламы, станут покупать больше. Теперь маркетологу нужно проводить A/B тестирование обоих креативов, чтобы выяснить, какой текст объявления лучше работает. При высоком уровне достоверности данные условия позволят учитывать результаты такого тестирования.
Проверка статистических гипотез
В случаях, когда информация говорит о незначительных изменениях в сравнении с предыдущими значениями, требуется проверка гипотез. Она позволяет определить, действительно ли происходят изменения или это всего лишь результат неточности измерений.
Для этого принимают или отвергают нулевую гипотезу. Задача решается на основании соотношения p-уровня (общей статистической значимости) и α (уровня значимости).
- p-уровень < α – нулевая гипотеза отвергается;
- p-уровень > α – нулевая гипотеза принимается.
Чем меньше значение p-уровня, тем больше шансов, что тестовая статистика актуальна.
Критерии оценки
Уровень значимости для определения степени правдивости полученных результатов обычно устанавливается на отметке 0,05. Таким образом, интервал вероятности между разными вариантами составляет 5%.
После этого необходимо найти подходящий критерий, по которому будут оцениваться выдвинутые гипотезы: односторонний или двусторонний. Для этого применяют разные методы расчета:

- t-критерий Стьюдента;
- u-критерий Манна-Уитни;
- w-критерий Уилкоксона;
- критерий хи-квадрата Пирсона.
T-критерий Стьюдента
предполагает сравнение данных по двум вариантам исследования и позволяет делать выводы о том, по каким параметрам они отличаются. Метод актуален, когда есть сомнения, что данные располагаются ниже или выше относительно нормального распределения.
Установить, все ли данные лежат в заданном пределе, можно с помощью специальной таблицы значений. Но чаще применяют автоматический расчет t-критерия Стьюдента. Существует много калькуляторов, которые работают по схожему принципу:
- Указываем вид расчета (связанные выборки или несвязанные).
- Вносим данные о первой выборке в первую колонку, о второй – во вторую. В одну строку вписываем одно значение, без пропусков и пробелов. Для отделения дробной части от основной используется точка.
- После заполнения обеих колонок, нажимаем кнопку запуска.
Преимущество коэффициента Стьюдента в том, что он применим для любой сферы деятельности, поэтому является самым популярным и используется на практике чаще всего.
Критерий Манна-Уитни
Рассчитывается по иному алгоритму, но предполагает использование аналогичных исходных данных. Его также зачастую рассчитывают онлайн с помощью специальных сервисов.
При расчете критерия Манна-Уитни есть особенности. Показатель применим для малых выборок или выборок с большими выбросами данных. Чем меньше совпадающих значений в выборках, тем корректнее будет работать критерий.
W-критерий Уилкоксона
Непараметрический аналог t-критерия Стьюдента для сравнения показателей до и после эксперимента, основанный на рангах. Его принцип заключается в том, что для каждого участника определяется величина изменения признака. Затем все значения упорядочиваются по абсолютной величине, рангам присваивается знак изменения, после чего «знаковые ранги» суммируются. Данный критерий применяется в медицинской статистике для сравнения показателей пациентов до лечения и после его завершения.
Критерий хи-квадрата Пирсона
Еще один непараметрический метод для оценки уровня значимости двух и более относительных показателей. Применяется для анализа таблиц сопряженности, в которых приведены данные о частотах различных исходов с учетом фактора риска.
Проблема множественного тестирования гипотез
Если сравнивать группы по различным срезам аудитории или метрикам, может возникать проблема множественного тестирования. Дело в том, что учесть абсолютно все проверки достаточно сложно. Это связано со сложностью предварительного прогнозирования их количества. К тому же, зачастую они всё равно не независимы.
Не существует универсального рецепта решения проблемы множественного тестирования гипотез. Аналитики рекомендуют руководствоваться здравым смыслом. Если протестировать много срезов по различным метрикам, любое исследование может показать якобы значимый для статистики результат. Это означает, итоги тестирования следует читать и интерпретировать с осторожностью.
Вычисление объема выборки и стандартного отклонения
После вычисления критерия оценки (критерия Стьюдента или Манна-Уитни) можно определить, какого оптимального объема должна быть выборка. При этом условии должно быть достаточное для признания достоверности результатов исследования количество людей в фокус-группах, на которых будут проверяться разные варианты.
Недостаточное количество участников эксперимента может стать причиной нехватки выборочных данных для того, чтобы сделать статистически значимый вывод и привести к повышению риска получения случайных результатов.
Объем выборки определяют с помощью статистической мощности (распространенный порог находится на уровне 80%). Этот показатель рассчитывают обычно с помощью специального калькулятора.
Затем можно переходить к вычислению уровня стандартного отклонения, по которому можно узнать величину разброса данных. Его рассчитывают по формуле:

s = √∑((xi – µ)2/(N – 1)), где:
xi – i-е значение или полученный результат эксперимента;
µ – среднее значение для конкретной исследуемой группы;
N – общее количество данных.
Для упрощения расчетов также используют онлайн-калькуляторы.
Значение p-уровня
Имея две гипотезы – нулевую и альтернативную, необходимо доказать одну из них (истинную) и опровергнуть другую (ложную).
Для этого основатель теории статистической значимости доктор Рональд Фишер создал определитель, с помощью которого можно было оценить, был эксперимент удачным или нет. Такой определитель получил название индекс достоверности или p-уровень (p-value).
P-уровень или уровень статистической значимости результатов – это показатель, который находится в обратной зависимости от истинного результата и отражает вероятность его ошибочной интерпретации.
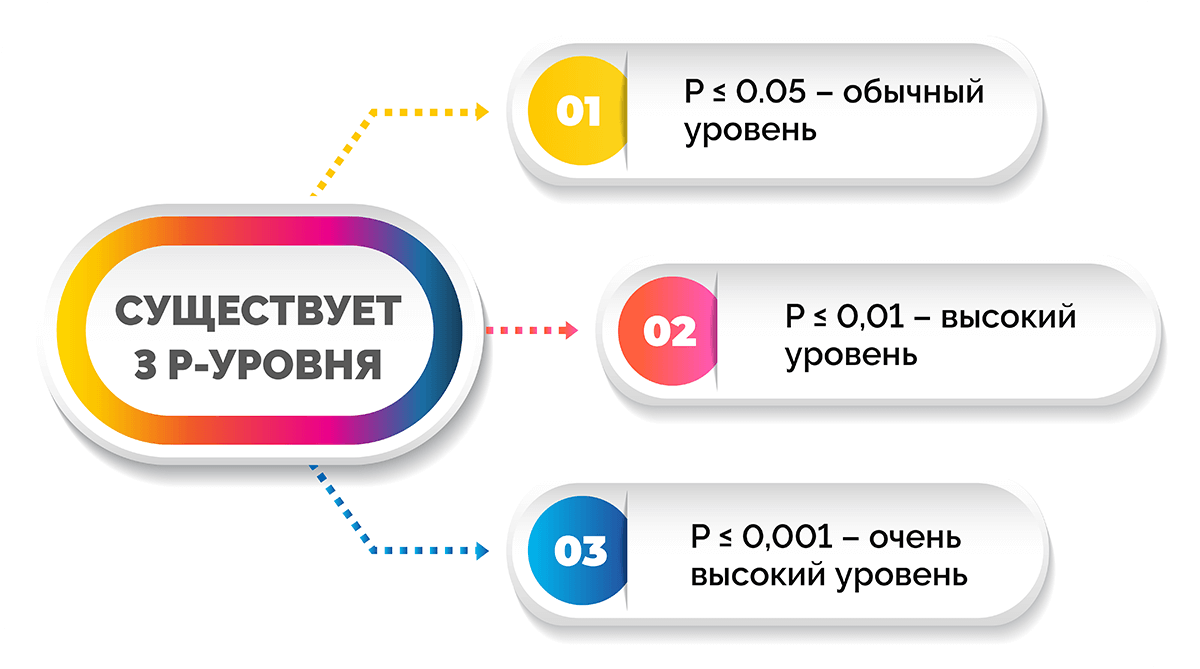
Существует 3 p-уровня.
- P ≤ 0,05 – обычный уровень, т. е. получен статистически значимый результат.
- P ≤ 0,01 – высокий уровень, т. е. выявлена выраженная закономерность.
- P ≤ 0,001 – очень высокий уровень.
Есть и другие значения статистической значимости. Например, уровень p ≥ 0,1 свидетельствует о том, что итог эксперимента не является статистически значимым.
Приближенные к статистически значимым результаты с уровнями p = 0,06 ÷ 0,09 говорят о том, что есть тенденция к существованию искомой закономерности.
Говоря проще, чем ниже значение p-уровня, тем более статистически значимым будет результат эксперимента и тем ниже вероятность ошибки.
Расчет статистической значимости
Выше в статье мы рассматривали порядок оценки уровня статистической значимости. Что касается расчета, то вручную он выполняется редко. Большинство аналитиков определяют уровень значимости с помощью онлайн-калькулятора.
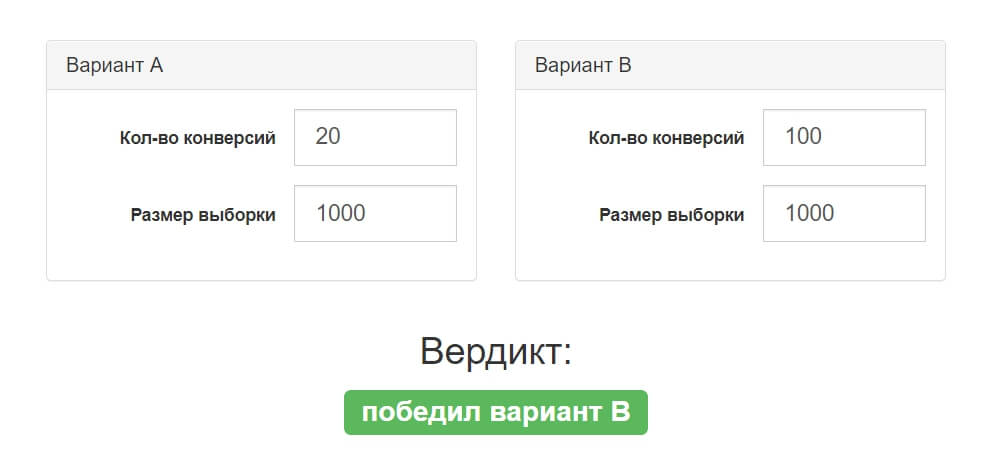
В анализе участвуют две гипотезы, для каждой из которых необходимо задать количество конверсий и размер выборки. Сервис автоматически рассчитывает показатель и определяет уровень значимости результата.
Порог вероятности
Основа статистической значимости – это вероятность получения нужного значения, если принять как факт, что нулевая гипотеза верна. Если предположить, что в процессе эксперимента было получено некое число Х, то при помощи функции плотности вероятности можно узнать, будет ли вероятность получить значение Х или любое другое значение с меньшей вероятностью, чем Х.
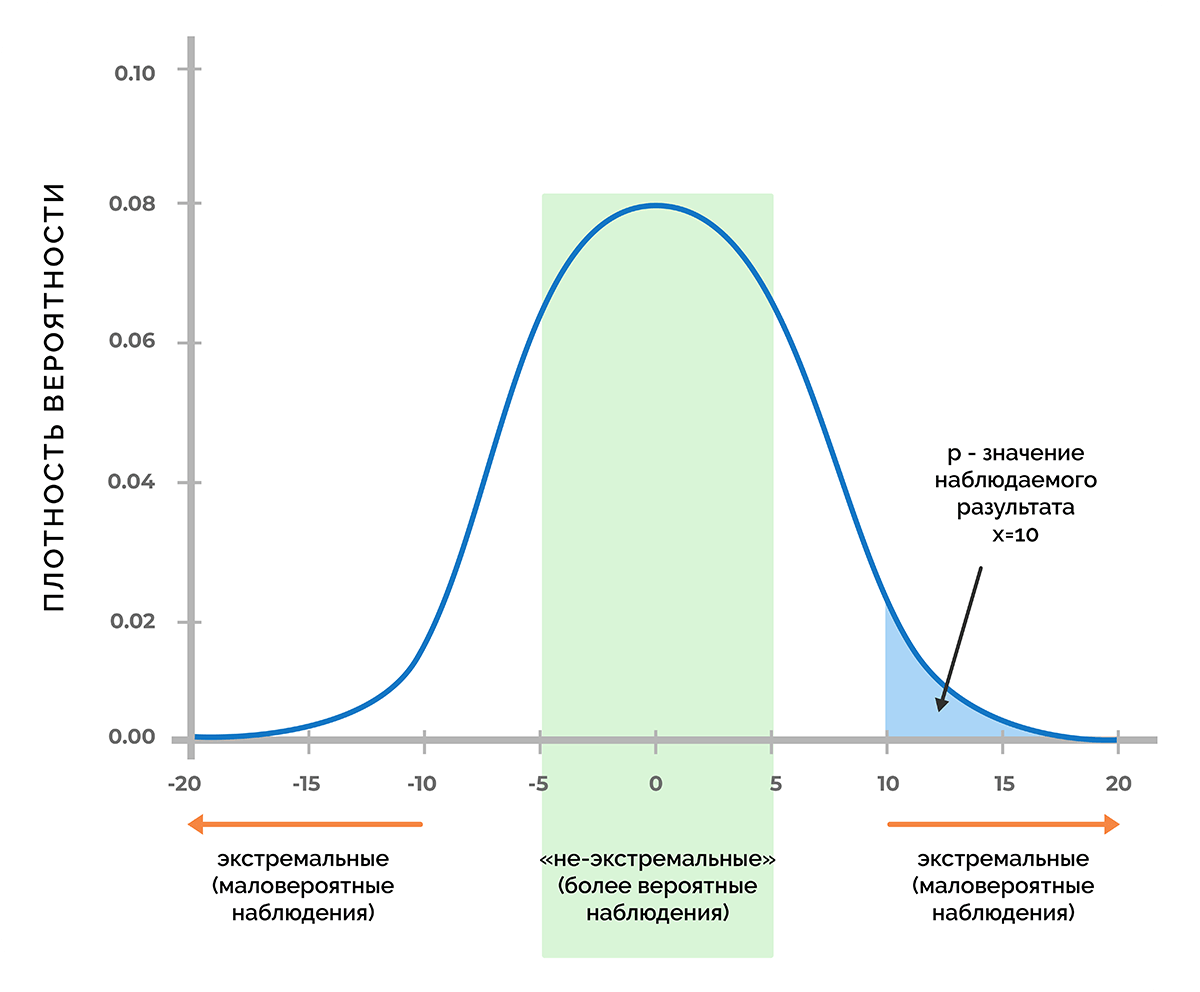
На рисунке изображена кривая Гаусса, соответствующая функции плотности вероятности, которая отвечает распределению значений показателя, при котором верна нулевая гипотеза.
При достаточно низком значении p-уровня не имеет смысла продолжать считать, что переменные не связаны друг с другом. Это позволяет отвергнуть нулевую гипотезу и принять факт того, что связь существует.
Пороги значимости в разных областях могут значительно отличаться. Так, при исследовании вероятности существования бозона Хиггса p-значение равно 1/3,5 млн, в сфере исследования геномов его уровень может достигать 5×10-8.
Статистическая значимость в A/B тестах
Одной из сфер широкого применения статистической значимости является маркетинг. Аналитики используют исследования для поиска оптимальных путей развития бизнеса, интернет-маркетологи оценивают эффективность рекламных кампаний и посещаемость ресурсов.
A/B тестирование – самый распространенный способ оптимизации страниц сайтов. Его результат невозможно предугадать, можно лишь строить алгоритм работы так, чтобы в конце тестирования получить максимальное количество данных, которые позволят сделать вывод о самом удачном варианте.
Важно, чтобы A/B тестирование длилось минимум 7 дней. Это позволит учесть колебания уровней конверсии и других показателей в разные дни.
Процедура A/B тестирования кажется довольно простой:
- Создается две веб-страницы (оригинальная и новая).
- Трафик делится между двумя версиями веб-страницы случайным образом.
- Собираются данные о каждой версии страницы.
- Данные анализируются и выбирается вариант с лучшими показателями, а второй отключается.
Важно, чтобы тестирование было достоверным, в противном случае неверное решение может привести к негативным последствиям для сайта.
В данном случае гипотезой считается достижение нужной достоверности. Сама достоверность будет статистической значимостью. Для тестирования гипотезы нужно сформулировать нулевую гипотезу и оценить возможность ее отклонения из-за малой вероятности.
Возможные ошибки
На этапе оценки результатов тестирования можно допустить два типа ошибок:
- ошибка первого рода (type I error) – ложноположительный итог, когда кажется, что различия между показателями двух тестируемых страниц есть, на самом же деле их нет;
- ошибка второго рода (type II error) – ложноотрицательный итог, когда существенная разница между тестируемыми страницами не заметна, но на самом деле она есть, при этом в тестировании видимое ее отсутствие является случайностью.
Как избежать ошибок
Избежать обоих типов ошибок можно, устанавливая при тестировании правильный размер выборки. Чтобы его определить, предстоит в настройках теста задать несколько параметров.
- Чтобы исключить ложноположительные результаты, понадобится указать уровень значимости. Обычно задают значение 0,05, которое будет гарантировать достоверность, превышающую 95%.
- Чтобы избежать ложноотрицательных результатов потребуется минимальная разница в ответах и вероятность обнаружить эту разницу, т. е. статистическая мощность. Последнюю по умолчанию устанавливают на уровне 80%.
Этого достаточно, чтобы вычислить требуемый размер выборки. Обычно расчеты проводятся с помощью спец. калькуляторов.
Можно ли доверять результатам на 100%
К сожалению, даже при правильно проведенной проверке гипотез могут быть допущены ошибки. Это связано с человеческим фактором, а точнее – со скрытыми предположениями, которые зачастую не имеют ничего общего с реальностью.
Вот распространенные предположения, которые приводят к ошибкам:
- посетители сайта, которые просматривают разные варианты веб-страницы, не связаны друг с другом;
- для всех посетителей вероятность конверсии одинакова;
- показатели, которые измеряются в процессе тестирования, имеют нормальное распределение.
На что обратить внимание
Без A/B теста сложно представить развитие современного интернет-продукта. Однако, несмотря на кажущийся простым инструмент, специалисты порой на практике встречаются с подводными камнями. Если знать о них заранее, можно повысить точность тестирования.
Первый узкий момент – проблема подглядывания. Наблюдение за итогами тестирования в реальном времени выступает в качестве соблазна для активных действий, предпринимаемых раньше времени. Обработка «сырых» данных неизменно приводит к статистической погрешности. Чем чаще смотреть на промежуточные результаты A/B теста, тем больше вероятность обнаружить разницу, которой в действительности нет:
- 2 подглядывания с желанием завершить тестирование повышают p-значение в 2 раза;
- 5 подглядывания – в 3,2 раза;
- 10 000 подглядываний – в 12 раз и более.
Решить проблему подглядывания можно тремя способами:
- Заблаговременно фиксировать размер выборки и не смотреть итоги теста до его окончания.
- С помощью математических методов: комбинация Sequential experiment design и байесовского подхода к A/B-тесту.
- С помощью продуктового метода, который предполагает предварительную оценку размера выборки, обеспечивающего эффективность тестирования, и принятие во внимание природы проблемы подглядывания в процессе промежуточных проверок.
Еще один подводный камень заключается в том, что от выигравшей гипотезы ожидают слишком многого. На самом деле в долгосрочной перспективе показатели победителя могут быть менее выдающимися, чем те, которые выдал тест.
Пример статистической значимости
Предположим, разработчики онлайн-игры тестируют два дизайна интерфейса. При A/B тестировании было привлечено 2000 новых игроков: по 1000 пользователей в каждую версию.
В первый день тестирования первая версия дизайна получила 370 возвратов пользователей, вторая – 510.
Как видно, вторая версия дизайна показала лучший результат возвратов. Но разработчики не были уверены, действительно ли это произошло из-за изменения продукта, а не стало следствием случайной погрешности.
Чтобы выяснить это, было принято решение рассчитать уровень значимости для наблюдаемой разницы. Поскольку метрика является простой, можно воспользоваться онлайн-сервисом и вычислить статистическую значимость автоматически.

P-значение < 0,001 в нашем примере свидетельствует о том, что при одинаковых тестовых группах вероятность увидеть наблюдаемую разницу чрезвычайно мала. Это говорит о том, что рост возвратов в первый день с высокой долей вероятности зависит от изменений продукта.
Часто задаваемые вопросы
Маркетинговые исследования статистики чаще всего проводятся путем A/B тестирования. О нем мы рассказали в одном из предыдущих разделов статьи. Однако при тестировании могут возникать некоторые трудности. Например, некорректное определение статистически значимого различия или невозможность определить, чем обусловлено различие. Решить подобные проблемы позволяет увеличение выборки и вариантов.
Оценка необходимости ранжирования данных статистики исключительно на основании статистической значимости может привести к серьезным ошибкам. Предпочтение лишь «значимых» результатов повышает риск искажения фактов.
В процессе тестирования регулярная проверка показателей с готовностью принять решение о завершении теста при обнаружении существенной разницы приводит к кумулятивному накоплению вероятных случайных моментов, при которых разница покидает пределы диапазона. В результате этого каждая новая проверка приводит к росту p-значения.
Заключение
Статистическая значимость является важным методом в ходе проведения экспериментов и исследований несмотря на риск ее неправильной интерпретации. При грамотном подходе погрешность можно свести к минимуму, используя значение в целях повышения достоверности результатов.
Олег Вершинин
Специалист по продукту
Все статьи автора
Нашли ошибку в тексте? Выделите нужный фрагмент и нажмите
ctrl
+
enter
Загрузить PDF
Загрузить PDF
Проверка гипотез проводится с помощью статистического анализа. Статистическую значимость находят с помощью Р-значения, которое соответствует вероятности данного события при предположении, что некоторое утверждение (нулевая гипотеза) истинно.[1]
Если Р-значение меньше заданного уровня статистической значимости (обычно это 0,05), экспериментатор может смело заключить, что нулевая гипотеза неверна, и перейти к рассмотрению альтернативной гипотезы. С помощью t-критерия Стьюдента можно вычислить Р-значение и определить значимость для двух наборов данных.
-
1
Определите свою гипотезу. Первый шаг при оценке статистической значимости состоит в том, чтобы выбрать вопрос, ответ на который вы хотите получить, и сформулировать гипотезу. Гипотеза — это утверждение об экспериментальных данных, их распределении и свойствах. Для любого эксперимента существует как нулевая, так и альтернативная гипотеза.[2]
Вообще говоря, вам придется сравнивать два набора данных, чтобы определить, схожи они или различны.- Нулевая гипотеза (H0) обычно утверждает, что между двумя наборами данных нет разницы. Например: те ученики, которые читают материал перед занятиями, не получают более высокие оценки.
- Альтернативная гипотеза (Ha) противоположна нулевой гипотезе и представляет собой утверждение, которое нужно подтвердить с помощью экспериментальных данных. Например: те ученики, которые читают материал перед занятиями, получают более высокие оценки.
-
2
Установите уровень значимости, чтобы определить, насколько распределение данных должно отличаться от обычного, чтобы это можно было считать значимым результатом. Уровень значимости (его называют также
-уровнем) — это порог, который вы определяете для статистической значимости. Если Р-значение меньше уровня значимости или равно ему, данные считаются статистически значимыми.[3]
- Как правило, уровень значимости (значение
) принимается равным 0,05, и в этом случае вероятность обнаружения случайной разницы между разными наборами данных составляет всего лишь 5%.
- Чем выше уровень значимости (и, соответственно, меньше Р-значение), тем достовернее результаты.
- Если вы хотите получить более достоверные результаты, понизьте Р-значение до 0,01. Как правило, более низкие Р-значения используются в производстве, когда необходимо выявить брак в продукции. В этом случае требуется высокая достоверность, чтобы быть уверенным, что все детали работают так, как положено.
- Для большинства экспериментов с гипотезами достаточно принять уровень значимости равным 0,05.
- Как правило, уровень значимости (значение
-
3
Решите, какой критерий вы будете использовать: односторонний или двусторонний. Одно из предположений в t-критерии Стьюдента гласит, что данные распределены нормальным образом. Нормальное распределение представляет собой колоколообразную кривую с максимальным количеством результатов посередине кривой.[4]
t-критерий Стьюдента — это математический метод проверки данных, который позволяет установить, выпадают ли данные за пределы нормального распределения (больше, меньше, либо в “хвостах” кривой).- Если вы не уверены, находятся ли данные выше или ниже контрольной группы значений, используйте двусторонний критерий. Это позволит вам определить значимость в обоих направлениях.
- Если вы знаете, в каком направлении данные могут выйти за пределы нормального распределения, используйте односторонний критерий. В приведенном выше примере мы ожидаем, что оценки студентов повысятся, поэтому можно использовать односторонний критерий.
-
4
Определите объем выборки с помощью статистической мощности. Статистическая мощность исследования — это вероятность того, что при данном объеме выборки получится ожидаемый результат.[5]
Распространенный порог мощности (или β) составляет 80%. Анализ статистической мощности без каких-либо предварительных данных может представлять определенные сложности, поскольку требуется некоторая информация об ожидаемых средних значениях в каждой группе данных и об их стандартных отклонениях. Используйте для анализа статистической мощности онлайн-калькулятор, чтобы определить оптимальный объем выборки для ваших данных.[6]
- Обычно ученые проводят небольшое пробное исследование, которое позволяет получить данные для анализа статистической мощности и определить объем выборки, необходимый для более расширенного и полного исследования.
- Если у вас нет возможности провести пробное исследование, постарайтесь на основании литературных данных и результатов других людей оценить возможные средние значения. Возможно, это поможет вам определить оптимальный объем выборки.
Реклама
-
1
Запишите формулу для стандартного отклонения. Стандартное отклонение показывает, насколько велик разброс данных. Оно позволяет заключить, насколько близки данные, полученные на определенной выборке. На первый взгляд формула кажется довольно сложной, но приведенные ниже объяснения помогут понять ее. Формула имеет следующий вид: s = √∑((xi – µ)2/(N – 1)).
- s — стандартное отклонение;
- знак ∑ указывает на то, что следует сложить все полученные на выборке данные;
- xi соответствует i-му значению, то есть отдельному полученному результату;
- µ — это среднее значение для данной группы;
- N — общее число данных в выборке.
-
2
Найдите среднее значение в каждой группе. Чтобы вычислить стандартное отклонение, необходимо сначала найти среднее значение для каждой исследуемой группы. Среднее значение обозначается греческой буквой µ (мю). Чтобы найти среднее, просто сложите все полученные значения и поделите их на количество данных (объем выборки).[7]
- Например, чтобы найти среднюю оценку в группе тех учеников, которые изучают материал перед занятиями, рассмотрим небольшой набор данных. Для простоты используем набор из пяти точек: 90, 91, 85, 83 и 94.
- Сложим вместе все значения: 90 + 91 + 85 + 83 + 94 = 443.
- Поделим сумму на число значений, N = 5: 443/5 = 88,6.
- Таким образом, среднее значение для данной группы составляет 88,6.
-
3
Вычтите из среднего каждое полученное значение. Следующий шаг заключается в вычислении разницы (xi – µ). Для этого следует вычесть из найденной средней величины каждое полученное значение. В нашем примере необходимо найти пять разностей:
- (90 – 88,6), (91- 88,6), (85 – 88,6), (83 – 88,6) и (94 – 88,6).
- В результате получаем следующие значения: 1,4, 2,4, -3,6, -5,6 и 5,4.
-
4
Возведите в квадрат каждую полученную величину и сложите их вместе. Каждую из только что найденных величин следует возвести в квадрат. На этом шаге исчезнут все отрицательные значения. Если после данного шага у вас останутся отрицательные числа, значит, вы забыли возвести их в квадрат.
- Для нашего примера получаем 1,96, 5,76, 12,96, 31,36 и 29,16.
- Складываем полученные значения: 1,96 + 5,76 + 12,96 + 31,36 + 29,16 = 81,2.
-
5
Поделите на объем выборки минус 1. В формуле сумма делится на N – 1 из-за того, что мы не учитываем генеральную совокупность, а берем для оценки выборку из числа всех студентов.[8]
- Вычитаем: N – 1 = 5 – 1 = 4
- Делим: 81,2/4 = 20,3
-
6
Извлеките квадратный корень. После того как вы поделите сумму на объем выборки минус один, извлеките из найденного значения квадратный корень. Это последний шаг в вычислении стандартного отклонения. Есть статистические программы, которые после введения начальных данных производят все необходимые вычисления.
- В нашем примере стандартное отклонение оценок тех учеников, которые читают материал перед занятиями, составляет s =√20,3 = 4,51.
Реклама
-
1
Рассчитайте дисперсию между двумя группами данных. До этого шага мы рассматривали пример лишь для одной группы данных. Если вы хотите сравнить две группы, очевидно, следует взять данные для обеих групп. Вычислите стандартное отклонение для второй группы данных, а затем найдите дисперсию между двумя экспериментальными группами. Дисперсия вычисляется по следующей формуле: sd = √((s1/N1) + (s2/N2)).[9]
- sd — дисперсия между двумя группами.
- s1 — стандартное отклонение в группе 1, N1 — объем выборки в группе 1.
- s2 — стандартное отклонение в группе 2, N2 — объем выборки в группе 2.
- В нашем примере предположим, что объем выборки в группе 2 (учащиеся, которые не читают материал перед занятиями) равен 5, а стандартное отклонение составляет 5,81. Находим дисперсию:
- sd = √((s1)2/N1) + ((s2)2/N2))
- sd = √(((4,51)2/5) + ((5,81)2/5)) = √((20,34/5) + (33,76/5)) = √(4,07 + 6,75) = √10,82 = 3,29.
-
2
Найдите t-оценку данных. Эта величина дает возможность перевести данные в форму, которая позволяет сравнить их с другими данными. t-оценки позволяют проверить t-критерий и найти, насколько вероятности двух групп отличаются друг от друга. Для вычисления t-оценки используется следующая формула: t = (µ1 – µ2)/sd.[10]
- µ1 — среднее значение для первой группы.
- µ2 — среднее значение для второй группы.
- sd — дисперсия между двумя выборками.
- В качестве µ1 используйте большее среднее значение, чтобы t-оценка не получилась отрицательной.
- В нашем примере предположим, что среднее значение для группы 2 (те, кто не читает) составляет 80. Находим t-оценку: t = (µ1 – µ2)/sd = (88,6 – 80)/3,29 = 2,61.
-
3
Определите степень свободы сделанной выборки. В случае t-оценки степень свободы определяется по объему выборки. Сложите объемы двух выборок и вычтите из суммы 2. В нашем примере степень свободы (с.с.) равна 8, поскольку первая и вторая выборки содержат по пять значений: (5 + 5) – 2 = 8.[11]
-
4
Оцените значимость по таблице значений критерия Стьюдента (t-критерия). Эту таблицу [12]
и степени свободы можно найти в справочнике по статистике или интернете. Отыщите строку, в которой содержится найденная вами степень свободы, и определите соответствующее t-оценке Р-значение.- При степени свободы 8 и t-оценке 2,61 Р-значение для одностороннего критерия попадает между 0,01 и 0,025. Поскольку мы выбрали уровень значимости 0,05, наши данные являются статистически значимыми. Ввиду этого мы отказываемся от нулевой гипотезы и принимаем альтернативную гипотезу, которая гласит:[13]
те ученики, которые читают материал перед занятиями, получают более высокие оценки.
- При степени свободы 8 и t-оценке 2,61 Р-значение для одностороннего критерия попадает между 0,01 и 0,025. Поскольку мы выбрали уровень значимости 0,05, наши данные являются статистически значимыми. Ввиду этого мы отказываемся от нулевой гипотезы и принимаем альтернативную гипотезу, которая гласит:[13]
-
5
Подумайте о том, чтобы продолжить исследования. Многие ученые сначала проводят небольшое пробное исследование с малым количеством измерений, чтобы понять, как следует организовать более крупное исследование. Расширенное исследование с большим числом измерений позволит вам повысить достоверность сделанных выводов.
Реклама
Советы
- Статистика представляет собой обширную и сложную науку. Занятия на специализированных курсах статистики помогут вам лучше понять концепцию статистической значимости.
Реклама
Предупреждения
- Приведенный анализ относится к t-критерию, который позволяет оценить разницу между двумя группами данных с нормальным распределением. Для более сложных наборов данных могут понадобиться другие критерии и методы.
Реклама
Об этой статье
Эту страницу просматривали 67 490 раз.
Была ли эта статья полезной?
Определение статистической значимости
Статистическая значимость – это вероятность того, что наблюдение не вызвано ошибкой выборки. Это подразумевает, что наблюдение имеет определенную причину. Следовательно, чтобы считать наблюдение статистически значимым, оно должно пройти тестирование.
Чтобы доказать статистическую значимость, набор данных должен отклонить нулевую гипотезу. Нулевая гипотеза. абсолютная истина и всегда прав. Таким образом, даже если выборка будет взята из генеральной совокупности, результат, полученный при изучении выборки, будет таким же, как и предположение. Читать далее. Чтобы доказать ошибочность нулевой гипотезы, p-значение наблюдения должно быть меньше уровня значимости. p-valueP-valueP-Value, или значение вероятности, является решающим фактором для нулевой гипотезы для вероятности того, что предполагаемый результат окажется истинным, будет принят или отклонен, и принятия альтернативного результата в случае отклонения предполагаемых результатов. . Читать дальше — это вероятность того, что наблюдение вызвано случайными факторами.
Оглавление
- Определение статистической значимости
- Понимание уровней статистической значимости
- Тест статистической значимости (P-значение)
- #1 – Статистическая проверка гипотез
- # 2 — Статистически значимое значение p
- Расчет статистической значимости
- Статистическая и практическая значимость
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи
- Статистическая значимость показывает, что наблюдение вызвано конкретной причиной, а не случайным фактором.
- Уровень значимости представлен α. Исследователь устанавливает его значения и обычно составляет 0,01, 0,05 или 0,1.
- Нулевая гипотеза предполагает, что исследование ложно. Однако альтернативная гипотеза, являющаяся предположением исследователя, может оказаться верной, отвергнув нулевую гипотезу.
- Условное значение α = 0,05. Следовательно, если значение p для набора данных ≤ 0,05, то результат статистически значим. Если p-значение > 0,05, то исследование может быть статистически незначимым.
Понимание уровней статистической значимости
Статистическая значимость широко применяется исследователями в качестве инструмента количественного исследования для принятия решений. Этот инструмент применяется в различных областях, таких как бизнес, маркетинг, реклама, инвестиции и финансы.
Следующие два фактора определяют значимость.
- Размер образца: Количество наблюдений в огромной степени влияет на уровень значимости. Большой набор данных (обязательно рандомизированная выборка) часто устраняет ошибку выборкиОшибка выборкиФормула ошибки выборки используется для расчета статистической ошибки, которая возникает, когда человек, проводящий тест, не выбирает выборку, которая представляет всю рассматриваемую совокупность. Формула для ошибки выборки = Z x (σ /√n)подробнее.
- Размер эффекта: Корреляция между двумя наборами данных или переменными называется размером эффекта. Больший эффект sizeEffect SizeEffect size измеряет интенсивность взаимосвязи между двумя наборами переменных или групп. Он рассчитывается путем деления разницы между средними значениями, относящимися к двум группам, на стандартное отклонение. Это статистическая концепция. Следовательно, она подразумевает, что два разных исследования показывают очень похожие значения. Больший размер эффекта указывает на то, что данные статистически более значимы.
Значение альфа (α) представляет собой статистическую значимость. Традиционное значение альфы составляет 0,05, что составляет 5%. Он служит 95% порогом значимости. Это означает, что вероятность точности результата составляет 95%.
Для достижения статистической значимости должно выполняться хотя бы одно из заданных условий:
- Значение p должно быть ниже значения альфа.
- Значения нулевой гипотезы не должны иметь места в доверительном интервале.
Доверительный интервал Доверительный интервал Доверительный интервал относится к степени неопределенности, связанной с конкретной статистикой, и часто используется вместе с пределом погрешности. Доверительный интервал = среднее значение выборки ± критический фактор × стандартное отклонение выборки. read more относится к гарантированному диапазону, в который попадают фактические значения. Для p-значения 0,05, то есть 5%, оставшиеся 95% считаются доверительным интервалом.
Например, в июне 2020 г. ОСИНА Испытание не достигло статистической значимости по своей основной конечной точке. Об этом сообщило агентство Рейтер.
Тест статистической значимости (P-значение)
Статистическая значимость включает в себя нахождение результата и его проверку. Набор данных должен успешно отвергнуть нулевую гипотезу.
#1 – Статистическая проверка гипотез
Гипотеза – это предположение исследователя. Исследователи предполагают, что они получат тот или иной результат еще до проведения теста. Это предположение основано на взаимосвязи между различными переменными или наборами данных.
Два типа гипотез, используемых для анализа данных, следующие:
- Нулевая гипотеза: Теперь, если теория, предложенная исследователями, неверна, гипотеза исследователя считается недействительной. Это обозначается H0.
- Альтернативная гипотеза: Однако, если теория исследователя оказывается верной, она называется альтернативной гипотезой. Обозначается H1.
# 2 — Статистически значимое значение p
Значение p обозначает значение вероятности, то есть вероятность результата, являющегося результатом случайности или совпадения, а не фактов. Таким образом, уровень статистической значимости можно анализировать с помощью p-значения, которое находится в диапазоне от 0 до 1. Статистический результат считается точным, когда p-значение равно или меньше 0,05. Другими словами, вероятность того, что данные были получены случайно или случайно, составляет всего 5%.
Таким образом, тестирование приведет к следующим двум возможностям.
- p-значение ≤ 0,05: значение p, равное или меньшее 0,05, указывает на то, что нулевая гипотеза, вероятно, ложна. Таким образом, есть шансы, что результат будет более статистически значимым.
- р-значение > 0,05: Напротив, значение, превышающее 0,05, означает, что нулевая гипотеза кажется вероятной, и результат может быть статистически незначимым.
Расчет статистической значимости
Рассмотрим следующую задачу на основе гипотетического сценария. Самуэль, владелец парка развлечений, хочет, чтобы гости проводили больше времени в парке. Среднее время, проведенное 20 посетителями парка, составляет 199 минут. Сэмюэл решает установить новые аттракционы. Для теста порог значимости принят равным 5%, среднее значение выборки равно 200 минутам, а стандартное отклонение равно 200 минутам. На основе полученных данных проведите тест значимости для Сэмюэля.
Данные:
- µ = 199 минут
- п = 20
- µ остается 199 минут до установки новых аттракционов
- µ > 199 минут после установки новых аттракционов
- α = 5% или 0,05
- х = 200 минут
- σ = 200 минут
Расчет
Мы будем применять z-тест здесь,
Z = (x̄ — μ) / √ (σ2 / n)
Z = (200 – 199) / √(200 / 20)
Z = 1/3,16228
Z = 0,31623 = 0,3
Теперь давайте определим z-оценку или p-значение для данной z-таблицы:
Z0,000,10,20,30,40,00,500000,503990,507980,511970,51595
Таким образом, p-значение равно 0,51197.
Здесь, p-значение > α, т.е.., 0,51197 > 0,05
Следовательно, нулевая гипотеза может быть верной, и результат не является статистически значимым.
В качестве альтернативы пользователи могут выбирать из различных онлайн-калькуляторов для проведения тестов значимости.
Статистическая и практическая значимость
Статистическая значимость исключает случайное совпадение и указывает на то, что данные являются результатом определенной причины. Однако практическая значимость обнаруживает величину этого эффекта и его актуальность в реальном мире.
В то время как исследователи используют размер выборки и p-значение для установления статистической значимости, размер эффекта наборов данных указывает на практическую значимость.
Таким образом, получение статистической значимости без определения практической значимости было бы не очень полезным.
Часто задаваемые вопросы (FAQ)
Что такое статистическая значимость в исследованиях?
Тесты значимости широко используются в научных, экономических и медицинских исследованиях для определения надежности результатов тестов путем анализа шансов на истинность нулевой гипотезы.
Как определить статистическую значимость?
Шаги для расчета значимости следующие.
1. Найдите нулевую и альтернативную гипотезы, т. е. H0 и H1.
2. Предположим порог значимости или уровень значимости (α).
3. Получите образец и данные для проведения теста.
4. Запустите статистические тесты, такие как z-тест, T-тест, ANOVA или Chi-Square.
5. Проверьте, являются ли данные статистически значимыми, определив p-значение.
6. Интерпретируйте результат или завершите исследование.
Почему значимо значение p, равное 0,05?
Значение p, равное 0,05, представляет собой альфа, т.е. порог статистической значимости. Это граница вероятности, поэтому любое значение, выходящее за ее пределы, считается статистически незначимым. Если p-значение превышает 5%, это указывает на то, что более 5% значений вызваны случайностью. В результате набор данных нельзя использовать в качестве существенного доказательства причинно-следственной связи.
Рекомендуемые статьи
Это было Руководство по статистической значимости и ее значению. Здесь мы обсуждаем тесты значимости (значение p) и то, как понять его уровни, а также примеры и расчеты. Вы также можете ознакомиться со следующими статьями, чтобы узнать больше:
- Проверка гипотезы
- Степени свободы
- Тест хи-квадрат в Excel
При обосновании
статистического вывода следует решить
вопрос, где же проходит линия между
принятием и отвержением нулевой
гипотезы? В силу наличия в эксперименте
случайных влияний эта граница не может
быть проведена абсолютно точно. Она
базируется на понятии уровня
значимости . Уровнем значимости
называется
вероятность ошибочного отклонения
нулевой гипотезы. Или, иными словами,
уровень
значимости это
вероятность ошибки первого рода при
принятии решения. Для обозначения
этой вероятности, как правило, употребляют
либо греческую букву а, либо латинскую
букву Р. В
дальнейшем мы будем употреблять букву
Р.
Исторически
сложилось так, что в прикладных науках,
использующих статистику, и в частности
в психологии, считается, что низшим
уровнем статистической значимости
является уровень Р=
0,05; достаточным
— уровень Р
= 0,01 и высшим
уровень Р=
0,001. Поэтому
в статистических таблицах, которые
приводятся в приложении к учебникам по
статистике, обычно даются табличные
значения для уровней Р
= 0,05, Р
= 0,01 и Р
— 0,001. Иногда
даются табличные значения для уровней
Р= 0,025
и Р= 0,005.
Величины 0,05, 0,01 и
0,001 — это так называемые стандартные
уровни статистической значимости. При
статистическом анализе экспериментальных
данных психолог в зависимости от задач
и гипотез исследования должен выбрать
необходимый уровень значимости. Как
видим, здесь наибольшая величина, или
нижняя граница уровня статистической
значимости, равняется 0,05 — это означает,
что допускается пять ошибок в выборке
из ста элементов (случаев, испытуемых)
или одна ошибка из двадцати элементов
(случаев, испытуемых). Считается, что ни
шесть, ни семь, ни большее количество
раз из ста мы ошибиться не можем. Цена
таких ошибок будет слишком велика.
Заметим, что в
современных статистических пакетах на
ЭВМ используются не стандартные уровни
значимости, а уровни, подсчитываемые
непосредственно в процессе работы с
соответствующим статистическим
методом. Эти уровни, обозначаемые буквой
Р, могут
иметь различное числовое выражение в
интервале от 0 до 1, например, Р
= 0,7, Р
= 0,23 или Р
— 0,012. По-
60
нятно, что в первых
двух случаях полученные уровни значимости
слишком велики и говорить о том, что
результат значим нельзя. В то же время
в последнем случае результаты значимы
на уровне 12 тысячных. Это достоверный
уровень.
Правило принятия
статистического вывода таково: на
основании полученных экспериментальных
данных психолог подсчитывает по
выбранному им статистическому методу
так называемую эмпирическую статистику,
или эмпирическое значение. Эту величину
удобно обозначить как Чэип.
Затем
эмпирическая статистика Чит
сравнивается
с двумя критическими величинами, которые
соответствуют уровням значимости в 5%
и в 1% для выбранного статистического
метода и которые обозначаются как Ч
. Величины
ЧKf
находятся
для данного статистического метода по
соответствующим таблицам, приведенным
в приложении к любому учебнику по
статистике. Эти величины, как правило,
всегда различны и их в дальнейшем
для удобства можно назвать как Чкр[
и Чкр2.
Найденные
по таблицам величины критических
значений 4Kft
и 4ff7
удобно
представлять в следующей стандартной
форме записи:
4ff),
найденное
по таблицам Приложения для Р<0,05
(5.1)
4Kfl,
найденное
по таблицам Приложения для Р<0,0]
Подчеркнем, однако,
что мы использовали обозначения Чыя
и Чкр
как сокращение
слова «число». Во всех статистических
методах приняты свои символические
обозначения всех этих величин: как
подсчитанной по соответствующему
статистическому методу эмпирической
величины, так и найденных по соответствующим
таблицам критических величин. Например,
при подсчете рангового коэффициента
корреляции Спирмена (см. главу II,
раздел 11.3) по таблице 21 Приложения были
найдены следующие величины критических
значений, которые для этого метода
обозначаются греческой буквой р (ро).
Так для Р =
0,05 по таблице 21 Приложения найдена
величина ркр1
= 0,61 и для
/’=0,01 величина р , = 0,76.
г>
«Г
—
В принятой в
дальнейшем изложении стандартной форме
записи это выглядит следующим образом:
61
Р = 0,61 для Р
< 0,05
0,76 для Р<
0,01 (5.2)
Теперь нам необходимо
сравнить наше эмпирическое значение
с двумя найденными по таблицам критическими
значениями. Лучше всего это сделать,
расположив все три числа на так называемой
«оси значимости». «Ось значимости»
представляет собой прямую, на левом
конце которой располагается 0, хотя он,
как правило, не отмечается на самой этой
прямой, и слева направо идет увеличение
числового ряда. По сути дела это привычная
школьная ось абсцисс ОХ
декартовой
системы координат. Однако особенность
этой оси в том, что на ней выделено три
участка, «зоны». Левая зона называется
зоной незначимости, правая — зоной
значимости, а промежуточная зоной
неопределенности. Границами всех
трех зон являются V
л
для Р =
0,05 и £/
з для Р = 0,01,
как это показано ниже:
Ось значимости
Подсчитанное Чзт
по какому
либо статистическому методу должно
обязательно опасть в одну из трех зон.
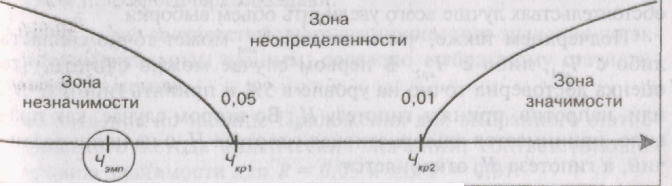
I.
Пусть Ч]мп
попало в
зону незначимости, тогда рисунок
выглядит так:
62
В этом
случае принимается гипотеза H0
об отсутствии различий.
2. Пусть
Ч
попало
в зону значимости, тогда рисунок выглядит
так:
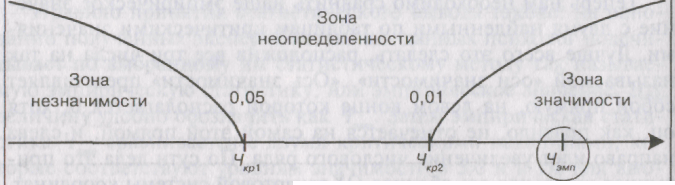
В этом
случае принимается альтернативная
гипотеза Я, о наличии различий, а
гипотеза Н0
отклоняется.
3. Пусть
Ч
эмп
попало
в зону неопределенночсти, тогда рисунок
выглядит
так:
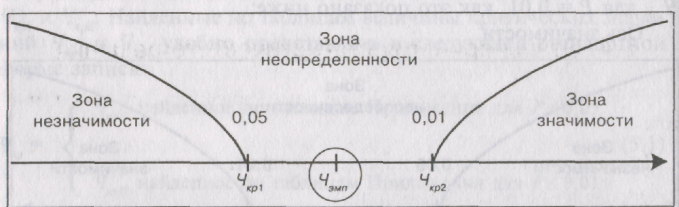
В этом
случае перед психологом стоит дилемма.
Так, в зависимости от важности решаемой
задачи он может считать полученную
статистическую оценку достоверной на
уровне 5%, и принять, тем самым гипотезу
Я,, отклонив гипотезу Я0,
либо — недостоверной на уровне 1%, приняв
тем самым, гипотезу Я0.
Подчеркнем, однако, что это именно
тот случай, когда психолог может допустить
ошибки первого или второго рода. Как
уже говорилось выше, в этих обстоятельствах
лучше всего увеличить объем выборки.
Подчеркнем
также, что величина Чгт
может
точно совпасть либо с У ,, либо с Чкр2.
В
первом случае можно считать, что оценка
достоверна точно на уровне в 5% и принять
гипотезу Яр
или,
напротив, принять гипотезу Я(|,
Во втором случае, как правило,
принимается альтернативная гипотеза
Я, о наличии различий, а гипотеза Я0
отклоняется.
63
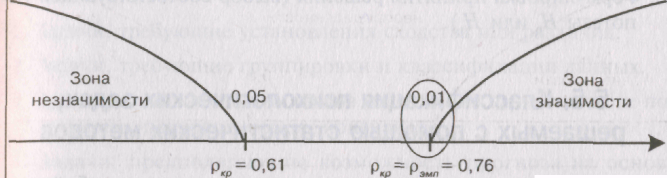
Для иллюстрации
этих положений строим соответствующую
«ось значимости» рассмотренного выше
примера для оценки уровня значимости
эмпирически рассчитанного рангового
коэффициента корреляции Спирмена.
Как
видим, в этом случае рк
= рыл,
следовательно
принимается альтернативная гипотеза
Я. о наличии различий, а гипотеза
H0
отклоняется.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Статистическая значимость часто применяется в маркетинге. С ее помощью определяют правильность выдвинутых предположений и вероятность их результатов. Она позволяет сделать выбор среди представленных теорий, что приводит к получению отличных результатов на практике.
Что такое статистическая значимость
Суть статистической значимости состоит в определении того, существует ли реальное основание в разнице между выбранными для исследования показателями, или это случайность? С данным понятием тесно связаны «нулевая» и «альтернативная» гипотезы.
Для лучшего понимания термина «статистическая значимость» необходимо понять, что такое «проверка гипотез». Эти два термина тесно взаимосвязаны.
Гипотеза иначе называется теорией. После окончания ее разработки требуется установить порядок по сбору достаточного количества доказательств этой теории и собрать их. Существует два типа гипотез: нулевая и альтернативная.
Нулевая гипотеза представляет собой теорию, которая гласит, что внесение коррективов ничего не поменяет, то есть сравниваемые объекты равнозначны в своих свойствах и нет смысла что-либо менять. Суть исследования заключается в опровержении гипотезы.
Альтернативная (исследовательская) гипотеза подразумевает сравнение, в результате которого один объект показывает себя эффективнее, чем другой.
Статистическая значимость как количественный показатель требует оценки. Оценка проходит поэтапно.
Постановка эксперимента
Все начинается с формулировки гипотезы. При этом должно быть выдвижение и нулевой, и альтернативной гипотезы. Придется сравнивать два набора данных для выяснения схожести и отличий. Эти утверждения требуют подтверждения с помощью экспериментальных данных.
Установка уровня
Данный уровень представляет собой порог статистической значимости, который каждый устанавливает сам. Этот уровень носит название displaystyle alpha }alpha – уровня. Чаще всего, устанавливают значение в 0,05. Вероятность найти разницу составляет 5%. Чем выше уровень, тем достовернее результаты.
Когда нужна максимальная достоверность, стоит снизить значение с 0,05 до 0,01. Чаще всего, такие показатели применяют в производстве для выявления брака. Однако для большинства экспериментов достаточно значения в 0,05.
Решение об используемом критерии
После установки уровня требуется определить, какой критерий использовать: одно- или двусторонний. Здесь стоит опираться на t-критерии Стьюдента. Они показывают, насколько нормально распределены данные. Графически они представлены в виде колоколообразной кривой. Большее количество результатов расположено в середине.
Критерий Стьюдента позволяет математически проверить расположены ли данные в установленных пределах или же выпадают из нормального распределения.
Двусторонний критерий нужен, когда нет уверенности в том, что показатели находятся выше или ниже установленной нормы распределения.
Когда есть точная уверенность, в каком направлении может наблюдаться выход за пределы нормы, нужно использовать односторонний критерий.
Определение объема выборки
Здесь потребуется статистическая мощность. Она представляет собой вероятность, что при выбранном объеме будет получен ожидаемый результат. Распространенный порог — 80%. Для анализа можно использовать специальные онлайн-калькуляторы. Это позволит определить оптимальный объем выборки.
Часто проводят пробное исследование, которое позволяет получить данные для анализа и установить объем выборки. Когда такой возможности нет, стоит поискать в тематической литературе усредненные значения.
Вычисление стандартного отклонения
Стандартное отклонение показывает величину разброса данных. Оно позволяет сделать выбор о близости или отдаленности данных. Их вычисляют по следующей формуле: s = √∑((xi – µ)2/(N – 1)).
- s — стандартное отклонение;
- ∑ указывает на необходимость суммировать полученные данные по выборке;
- xi соответствует значению i, то есть отдельному полученному результату;
- µ — это среднее значение для данной группы;
- N — общее число данных в выборке.
Теперь потребуется отыскать среднее значение для каждой группы. Для этого суммируют средние значения каждой группы и делят на объем выборки.
Далее необходимо определить разницу (xi – µ). Для этого следует вычесть из найденной средней величины каждое полученное значение.
Теперь каждую полученную величину умножают на саму себя или возводят во вторую степень и суммируют величины. После этой операции не должно остаться отрицательных значений.
Следующий шаг — деление объема минус один. Делят полученную в предыдущем шаге сумму на величину, полученную от вычитания единицы. После этого извлекают квадратный корень из величины. Это и будет нужная величина стандартного отклонения.
Определение значимости
Для определения значимости потребуется взять две группы данных. Для последней вычисляют стандартное отклонение, после чего вычисляют дисперсию между обеими группами по формуле:
sd = √((s1/N1) + (s2/N2)).
- sd — дисперсия между двумя группами;
- s1 — стандартное отклонение в группе 1, N1 — объем выборки в группе 1;
- s2 — стандартное отклонение в группе 2, N2 — объем выборки в группе 2.
Необходимо определить t-оценку показателей для перевода полученных данных в стандартизированную форму, которая позволить провести сравнение с другими данными. Эта оценка делает возможным проверку t-критерия, а также выяснение величины отличия одной группы от другой. Для определения t-оценки применяют формулу: t = (µ1 – µ2)/sd:
- µ1 — среднее значение для первой группы;
- µ2 — среднее значение для второй группы;
- sd — дисперсия между двумя выборками.
Совет: первым используют большее среднее значение, чтобы итоговая величина не была отрицательной.
Далее требуется определить степень свободы выборки. Для этого вычисляют объем: суммируют объемы двух выборок и вычитают 2. Полученная величина станет окончательной. Ее оценивают по таблице значений критерия Стьюдента (t-критерия). Таблица представлена ниже.
Пользоваться представленной таблицей просто: находите строку в соответствии с полученной степенью свободы и определяете соответствующее t-оценке Р-значение.
Например, при степени свободы 8 и t-оценке 2,61 Р-значение для одностороннего критерия попадает между 0,01 и 0,025. При выбранном показателе в 0,05 эти данные попадают в категорию «статистически значимые». Это помогает сделать выбор в пользу альтернативной гипотезы и отказаться от нулевой.
Заключение
Определение статистической значимости помогает решать маркетинговые задачи и минимизировать риски. Такие расчеты часто проводятся при A/B тестированиях и помогают узнать, как будет вести себя клиент в будущем, окупится ли товар и т.д.
























