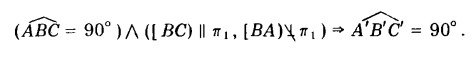Расстояния
Задача на нахождения расстояния в стереометрической фигуре является главной и самой важной из всех. Прежде всего определимся с тем, что имеется ввиду под словом «расстояние», ведь их может быть бесконечно много.
Расстояние между объектами в геометрии – это кратчайшее из расстояний между ними.
Обозначение:
В стереометрии найти расстояние можно между следующими комбинациями фигур:
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ
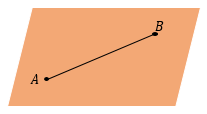
Расстояние между точками– это длина отрезка, соединяющего эти точки.
В задачах на стереометрию мы не можем просто воспользоваться линейкой, и длину этого отрезка должны найти аналитически. Поэтому длину отрезка AB между точками A и B находят как сторону треугольника, если отрезок AB удается включить в некоторый треугольник в качестве одной из его сторон.
То есть если в задаче предлагается найти расстояние между точками, нужно задать себе вопрос: «В каком треугольнике этот отрезок является стороной?», затем построить этот треугольник и найти в нем нужную сторону.
Например:
|
|
|
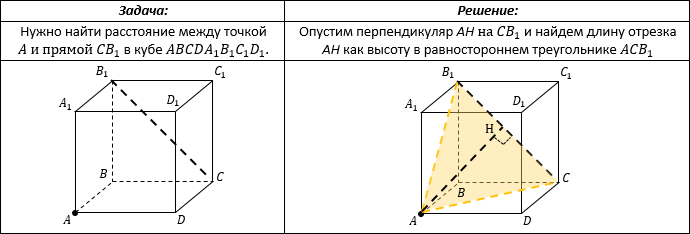
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПРЯМОЙ
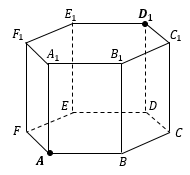
Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки на прямую.
Этот отрезок перпендикуляра можно вычислить, включив его в треугольник (или трапецию) в качестве одной из высот. То есть нужно задать себе вопрос: «В каком треугольнике этот отрезок является высотой?», затем построить этот треугольник и найти в нем высоту.
Например:
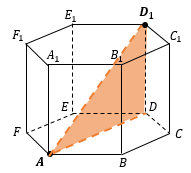
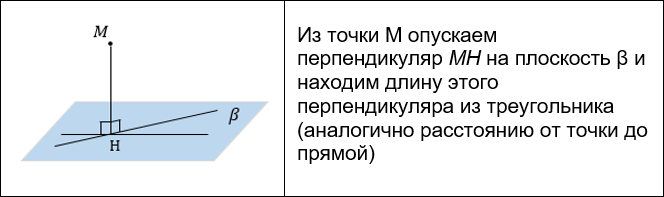
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПЛОСКОСТЬЮ
Существует несколько способов нахождения расстояния от точки до плоскости:
- Построение перпендикуляра из точки на плоскость.
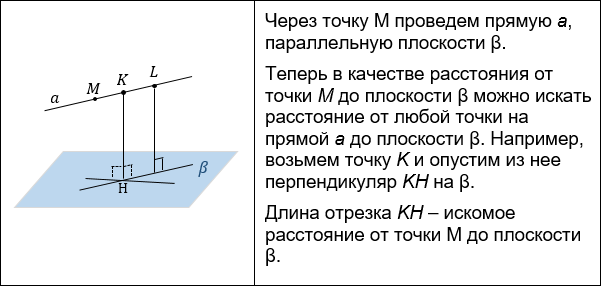
- К этому способу обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной линии с M.
- Построение перпендикуляра из точки прямой к плоскости.
- Построение перпендикуляра из точки плоскости на плоскость.
К этому способу, аналогично, обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной плоскости с M.
- Через двойное выражение объема.
Расстояние от точки M до плоскости β – это перпендикуляр, опущенный из точки на плоскость, то есть по сути это высота в некоторой пирамиде с вершиной M и плоскостью основания, лежащей на β. Если легко вычислить объем этой пирамиды, используя другое основание и другую высоту, то через этот объем можно найти нужное расстояние.
Например:
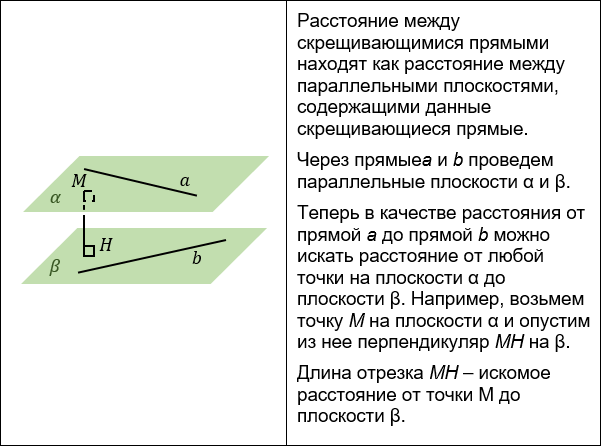
РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
Существует несколько способов нахождения расстояния между скрещивающимися прямыми:
1. Построение взаимного перпендикуляра.
2. Построение параллельной прямой.
К этому способу обращаются, если строить взаимный перпендикуляр неудобно и одна из скрещивающихся прямых уже заключена в удобную плоскость.
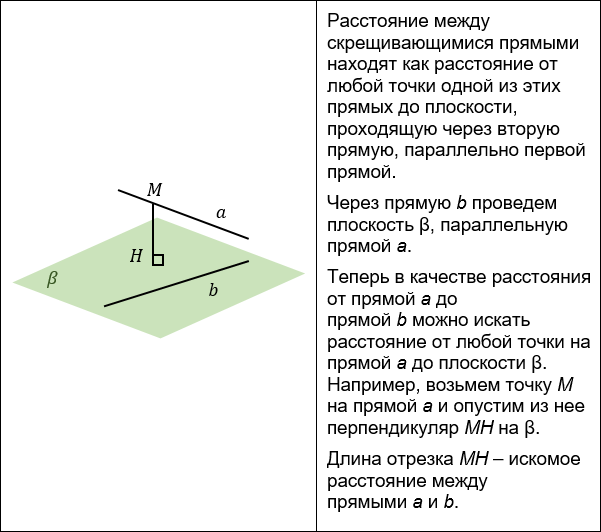
3. Построение параллельной плоскости.
Не будет преувеличением утверждать, что построение взаимно перпендикулярных прямых и плоскостей наряду с определением расстояния между двумя точками являются основными графическими операциями при решении метрических задач.
Теоретической предпосылкой для построения на эпюре Монжа проекций прямых и плоскостей, перпендикулярных по отношению друг к другу в пространстве, служит отмеченное раньше (см. § 6) свойство
проекции прямого угла, одна из сторон которого параллельна какой-либо плоскости проекции:
1. Взаимно перпендикулярные прямые.
Чтобы можно было воспользоваться отмеченным свойством для построения на эпюре Монжа двух пересекающихся под углом 90° прямых, необходимо, чтобы одна из них была параллельна какой-либо плоскости проекции. Поясним сказанное на примерах.
ПРИМЕР 1. Через точку А провести прямую l, пересекающую горизонталь h под прямым углом (рис. 249).
Так как одна из сторон h прямого угла параллельна плоскости π1 , то на эту плоскость прямой угол спроецируется без искажения. Поэтому через А’ проводим горизонтальную проекцию l’ ⊥ h’. Отмечаем точку М’ = l’ ∩ h’. Находим М» (М» ∈ h»). Точки А» и М» определяют l» (см. рис. 249, а).
Если вместо горизонтали будет задана фронталь f, то геометрические построения по проведению прямой l ⊥ f аналогичны только что рассмотренным с той лишь разницей, что построения неискаженной проекции прямого угла следует начинать с фронтальной проекции (см. рис. 249, б).
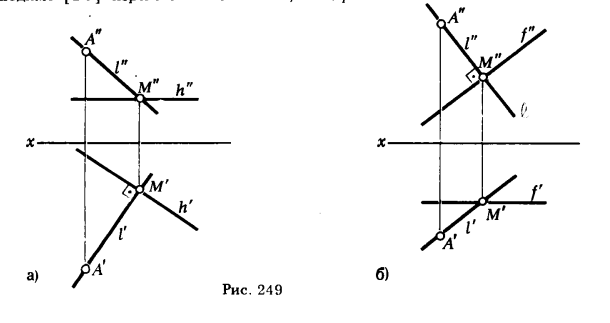
ПРИМЕР 2. Через точку А провести прямую l , пересекающую прямую а , заданную отрезком [ВС], под углом 90° (рис. 250).
Так как данный отрезок занимает произвольное положение по отношению к плоскостям проекций, мы не можем, как в предыдущем примере, воспользоваться свойством о частном случае проецирования прямого угла, поэтому вначале необходимо [ВС] перевести в положение, параллельное какой-либо плоскости проекции.
На рис. 250 [ВС] переведен в положение, параллельное плоскости π3. Это сделано с помощью способа замены плоскостей проекции путем замены плоскости π1 → π3 || [ВС].
В результате такой замены в новой системе x1π2/π3 [ВС] определяет горизонтальную прямую, поэтому все дальнейшие простроения выполнены так же, как это было сделано в предыдущем примере: после того, как была найдена точка М’1, ее перевели на исходные плоскости проекции в положение М» и М’, эти точки совместно с А» и А’ определяют проекции прямой l.
ПРИМЕР 3. Провести горизонтальную проекцию стороны [ВС] прямого угла АВС, если известны его фронтальная проекция ∠A»B»C» и горйзонтапьная проекция стороны [А’В’] (рис. 251).
РЕШЕНИЕ:
1. Переводим сторону угла [ВА] в положение || π3 путем перехода от системы плоскостей проекции хπ2/π1 к новой x1π3/π2
2. Определяем новую фронтальную проекцию [B»1A»1].
Из В»1 восставляем перпендикуляр к [В»1A»1]. На этом перпендикуляре определяем точку С»1 (С»1 удалена от оси x1 на расстояние |Сx1 С»1| = |СxС»|).
4. Горизонтальная проекция С’ определяется как точка пересечения прямых (С»1Сx1) ∩ (С»Сx) = С’.
2. Взаимно перпендикулярные прямая и плоскость.
Из курса стереометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна хотя бы к двум пересекающимся прямым, принадлежащим этой плоскости.
Если в плоскости взять не произвольные пересекающиеся прямые, а ее горизонталь и фронталь, то открывается возможность воспользоваться свойством проекции прямого угла, как это было сделано в примере 1, рис. 249.
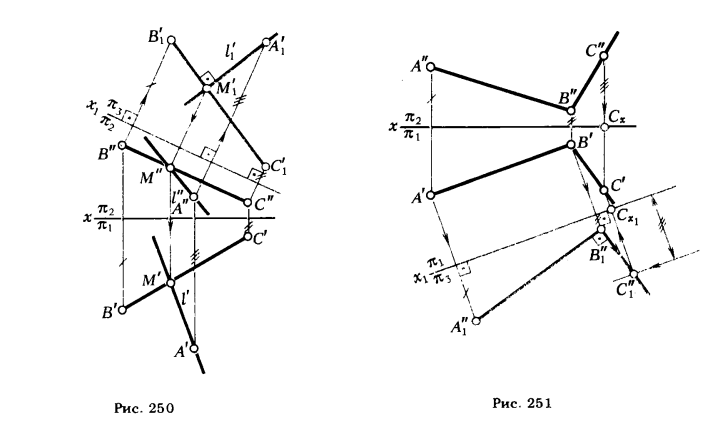
Рассмотрим следующий пример; пусть из точки A ∈ α требуется восставить перпендикуляр к плоскости α (рис. 252).
Через точку А проводим горизонталь h и фронталь f плоскости α. Тогда, по определению (АВ), перпендикулярная к плоскости α, должна быть перпендикулярна к прямым h и f, т. е. 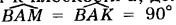
искажения, т. е.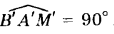
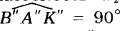
Если плоскость задана следами, то теорема может быть сформулирована иначе: для того чтобы прямая в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы проекции этой прямой были перпендикулярны к одноименным следам плоскости.
Установленные теоремой зависимости между прямой в пространстве, перпендикулярной к плоскости, и проекциями этой прямой к проекциям линий уровня (следам) плоскости лежат в основе графического алгоритма решения задачи по проведению прямой, перпендикулярной к плоскости, а также построения плоскости, перпендикулярной к заданной прямой.
ПРИМЕР 1. Восставить в вершине А перпендикуляр AD к плоскости ΔАВС (рис. 253).
Для того чтобы определить направление проекций перпендикуляра, проводим проекции горизонтали h и фронтали f плоскости ΔАВС. После этого из точки А’ восставляем перпендикуляр к h’, а из А» — к f’.
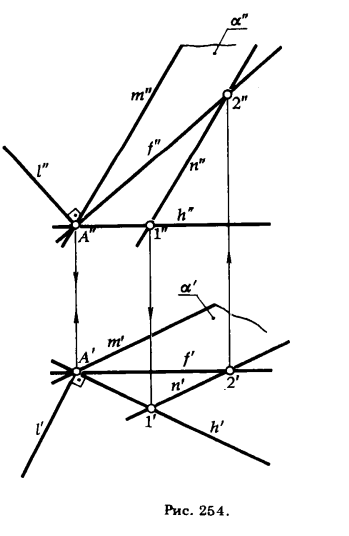
ПРИМЕР 2. Из точки А, принадлежащей плоскости α (m || n), восставить перпендикуляр к этой плоскости (рис. 254).
РЕШЕНИЕ. Для определения направления проекций перпендикуляра l’ и l», как и в предыдущем примере, проводим через точку А (А’,А») горизонталь h(h’, h»), принадлежащую плоскости α. Зная направление h’, строим горизонтальную проекцию перпендикуляра l’ (l’ ⊥ h’). Для определения направления фронтальной проекции перпендикуляра через точку А (А’, А») проводим фронталь f (f’, f») плоскости α. В силу параллельности f фронтальной плоскости проекции прямой угол между l и f проецируется на π2 без искажения, поэтому проводим l» ⊥ f».
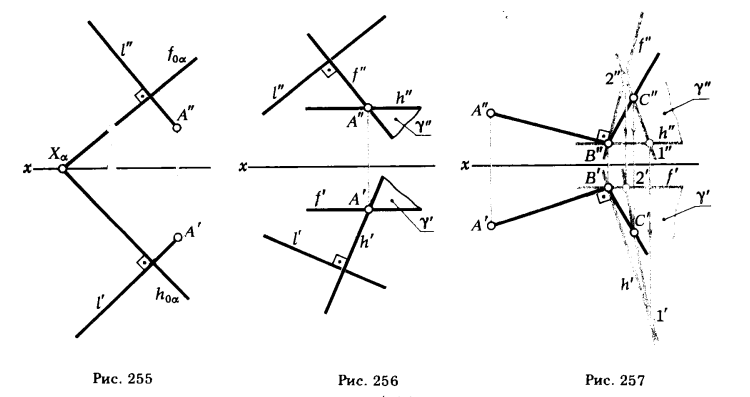
На рис. 255 эта же задача решена для случая, когда плоскость α задана следами. Для определения направлений проекций перпендикуляра отпадает необходимость в проведении горизонтали и фрон-
тали, так как их функции выполняют следы плоскости h0α и f0α. Как видно из чертежа, решение сводится к проведению через точки А’ и А» проекций l’ ⊥ h0α и l» ⊥ f0α.
ПРИМЕР 3. Построить плоскость γ, перпендикулярную к данной прямой l и проходящую через заданную точку А (рис. 256).
РЕШЕНИЕ. Через точку А проводим горизонталь h и фронталь f. Эти две пересекающиеся прямые определяют плоскость; чтобы она была перпендикулярна к прямой l, необходимо, чтобы прямые h и f составляли с прямой l угол 90°. Для этого проводим h’ ⊥ l’ и f» ⊥ l». Фронтальная проекция h» и горизонтальная проекция f’ проводятся параллельно оси x.
Рассмотренный случай позволяет по иному решать задачу, приведенную в примере 3 (с. 175 рис. 251). Сторона [ВС] ∠АВС должна принадлежать плоскости γ ⊥ [АВ] и проходить через точку В (рис. 257).
Это условие и определяет ход решения задачи, который состоит в следующем: заключаем точку В в плоскость γ ⊥ [АВ], для этого через точку В проводим горизонталь и фронталь плоскости γ так, чтобы h’ ⊥ A’B’ и f» ⊥ A»B».
Точка С ∈ (ВС), принадлежащей плоскости γ, поэтому для нахождения ее горизонтальной проекции проводим через С» произвольную прямую 1″2″, принадлежащую плоскости γ; определяем горизонтальную проекцию этой прямой 1’2′ и на ней отмечаем точку С’ (С’ определяется пересечением линии связи — перпендикуляра, опущенного из С», с горизонтальной проекцией прямой 1’2′). С’ совместно с В’ определяют горизонтальную проекцию (ВС) ⊥ (АВ).
3. Взаимно перпендикулярные плоскости..
Две плоскости перпендикулярны, если одна из них содержит прямую, перпендикулярную к другой плоскости.
Исходя из определения перпендикулярности плоскостей, задачу на построение плоскости β, перпендикулярной к плоскости α, решаем следующим путем: проводим прямую l, перпендикулярную к плоскости α; заключаем прямую l в плоскость β. Плоскость β ⊥ α, так как β ⊃ l ⊥ α.
Через прямую l можно провести множество плоскостей, поэтому задача имеет множество решений. Чтобы конкретизировать ответ, необходимо указать дополнительные условия.
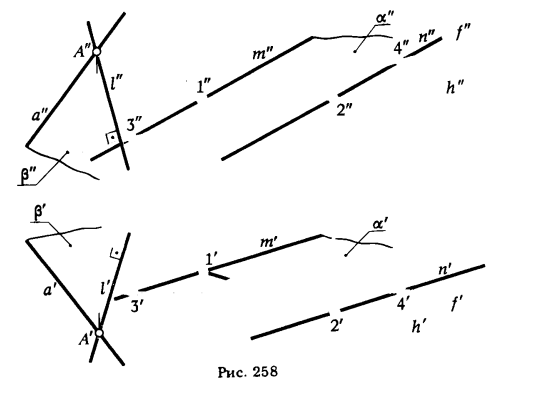
ПРИМЕР 1. Через данную прямую а провести плоскость β, перпендикулярную к плоскости α (рис. 258).
РЕШЕНИЕ. Определяем направление проекций перпендикуляра к плоскости α, для этого находим горизонтальную проекцию горизонтали (h’) и фронтальную проекцию фронтали (f») ; из проекций произвольной точки А ∈ α проводим проекции перпендикуляра l’ ⊥ h’ и l» ⊥ f». Плоскость β ⊥ α, так как β ⊃ l ⊥ α.
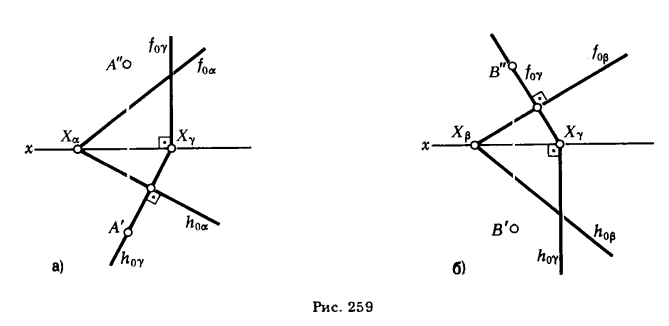
ПРИМЕР 2. Через данную точку А провести горизонтально проецирующую плоскость γ, перпендикулярную к плоскости α, заданной следами (рис. 259, а).
Искомая плоскость γ должна содержать прямую, перпендикулярную плоскости α, или быть перпендикулярной к прямой, принадлежащей плоскости α. Так как плоскость γ должна быть горизонтально проецирующей, то прямая, перпендикулярная к ней, должна быть параллельна плоскости π1, т. е. являться горизонталью плоскости α или (что то же самое) горизонтальным следом этой плоскости — h0α Поэтому через горизок тальную проекцию точки А’ проводим горизонтальный след h0γ ⊥ h0α фронтальный след f0γ ⊥ оси х.
На рис. 259, б показана фронтально проецирующая плоскость γ, проходящая через точку В и перпендикулярная к плоскости π2.
Из чертежа видно, что отличительной особенностью эпюра, на котором заданы две взаимно перпендикулярные плоскости, из которых одна — фронтально проецирующая, является перпендикулярность их фронтальных следов f0γ ⊥ f0α, горизонтальный след фронтально проецирующей плоскости перпендикулярен оси х.
Взаимно перпендикулярные прямые
Взаимно перпендикулярные прямые, пересекаясь имеют одну общую точку и образуют при этом плоский угол.
Если проекция некоторого угла, у которого одна сторона, параллельна плоскости проекции,
равна прямому углу, то и проецируемый угол также прямой.
Взаимно перпендикулярные прямые могут быть проведены на основе данного утверждения на эпюре Монжа: из двух
пересекающихся под прямым углом прямых, необходимо чтобы одна из них была параллельна какой-либо
плоскости проекции.
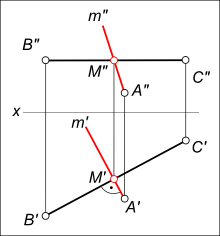
Через точку A провести прямую m перпендикулярную горизонтали h (на рисунке это отрезок [BC]) .
Взаимно перпендикулярные прямые
h` — это горизонтальная проекция прямой h параллельной плоскости проекции H. Принимая ее за одну сторону прямого угла, восстанавливаем из точки A` перпендикуляр m` и на их пересечении находим точку M`. По линии связи определяем недостающую проекцию M».
Через точку A провести прямую m ⊥[BC].
Взаимно перпендикулярные прямые
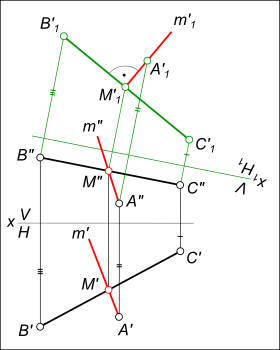
Судя по проекциям отрезка [B`C`], [B»C»], они принадлежат прямой [BC] общего положения. До того как опустить перпендикуляр из точки A на данную прямую, необходимо перевести ее в частное положение:
— [BC] ║ H, на эпюре: [B`C`] ║ x
или
— [BC] ║ V, на эпюре: [B»C»] ║ x.
Перевод осуществляем способом перемены плоскостей проекций — введя новую плоскость проекции H1, проведя ось x1 ║ [B»C»]. На H1 строим проекции отрезка [B`1C`1], которая представляет собой проекцию горизонтальной прямой и проекцию точки A`1. Из точки A`1, опуская перпендикуляр к [B`1C`1], находим точку M`1 и далее M», M` и m», m`.
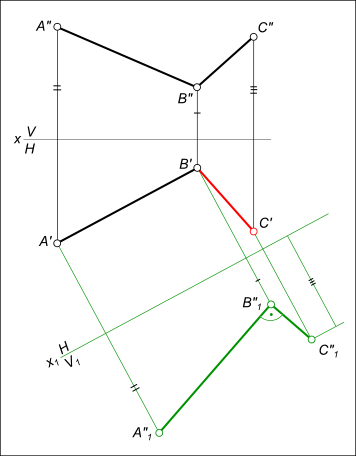
Провести недостающую горизонтальную проекцию стороны BC прямого угла ABC
Взаимно перпендикулярные прямые
+
Перпендикулярность векторов
Мы можем выяснить, будут ли два каких-либо вектора взаимно перпендикулярными. Для этого нужно воспользоваться координатами векторов и некоторыми приемами, описанными в данной статье. Информация о перпендикулярности будет полезной для решения некоторых задач физики и математики.
Координаты вектора на плоскости, равного по модулю и перпендикулярного данному
Пусть на плоскости заданы координаты какого-либо вектора. Из этих координат получим координаты двух дополнительных векторов, перпендикулярных первоначальному вектору. Все три вектора будут иметь равные длины и располагаться в плоскости xOy.
Алгоритм получения координат перпендикулярных векторов
Вектор на плоскости xOy, перпендикулярный данному вектору получают так:
- Поменять местами координатные числа «x» и «y».
- Заменить знак у одной из координат на противоположный.
Графический пример
Рассмотрим небольшой графический пример (рис. 1).
Рис. 1. На рисунке векторы, обозначенные черным цветом, перпендикулярны вектору, обозначенному красным цветом
На плоскости проведены три вектора: один красный и два черных и, отмечены их координаты. Рассмотрим подробнее координаты двух векторов: (vec{a}) и (vec{b}).
[ vec{a} = left{ 4 ; 3 right} ]
[ vec{b} = left{ -3 ; 4 right} ]
Из рисунка видно, что векторы (vec{a}) и (vec{b}) перпендикулярны: ( vec{a} perp vec{b} ).
Вектор ( -vec{b} = left{ 3 ; -4 right} ), также будет перпендикулярным вектору ( vec{a} ): ( vec{a} perp vec{(-b)} )
Векторы, изображенные черным цветом, перпендикулярны красному вектору.
Длины векторов ( vec{a} ), ( vec{b} ) и ( vec{(-b)} ) равны.
Условие перпендикулярности векторов
Взаимную перпендикулярность двух векторов можно проверить, вычислив их скалярное произведение. Этот способ проверки можно применять для векторов, расположенных как на плоскости, так и в трехмерном пространстве.
Векторы будут перпендикулярными, когда их скалярное произведение равно нулю.
Пусть, известны координаты двух векторов и пусть каждый вектор имеет ненулевую длину.
[ large boxed { begin{cases} vec{a} = left{ a_{x} ; a_{y} ; a_{z} right} \ vec{b} = left{ b_{x} ; b_{y} ; b_{z} right} \ |vec{a}| ne 0 \ |vec{b}| ne 0 end{cases}}]
Запишем условие перпендикулярности векторов.
Для двумерного случая:
[ large boxed { a_{x} cdot b_{x} + a_{y} cdot b_{y} = 0 }]
Для трехмерного случая:
[ large boxed { a_{x} cdot b_{x} + a_{y} cdot b_{y} + a_{z} cdot b_{z} = 0 }]
Пользуясь любой из этих формул, можно определить одну неизвестную координату вектора.
При этом, должны быть известными остальные координаты этого вектора и все координаты второго вектора.
Примечание:
Есть такое правило: Количество неизвестных должно равняться количеству уравнений.
Чтобы однозначно определить значение неизвестной, в уравнение должна входить только одна неизвестная. Остальные величины должны быть известными.
Перпендикулярные векторы в физике
В физике перпендикулярность некоторых векторов достаточно важна.
Вот несколько примеров:
- Если угол между вектором скорости тела и вектором силы, действующей на тело, будет прямым, то такая сила работу по перемещению тела совершать не будет.
- На проводник с током магнитное поле действует максимальной силой, когда вектор магнитной индукции и вектор тока в проводнике перпендикулярны.
- Когда угол между вращающей силой и, расстоянием между точкой приложения силы и осью вращения, будет прямым, вращательный момент будет максимальным.
- Между линейной скоростью точки колеса и расстоянием от этой точки до оси вращения, угол прямой (радиус и касательная перпендикулярны).
- На вращающееся тело действует центростремительная сила. Угол прямой между этой силой и линейной скоростью точки тела (радиус и касательная перпендикулярны).
Оценка статьи:
Загрузка…