Раньше мы изучили метод последовательного
конструирования алгоритмов, при котором алгоритм последовательно
разбивается на подзадачи, пока все они не станут понятны исполнителю.
При конструировании алгоритмов вы уже наверняка
сталкивались, с ситуацией, когда одна и та же последовательность действий
выполнялась для различных данных в разных местах программы, то есть одну и ту
же подзадачу решали несколько раз, так на пример в некоторых программах мы
несколько раз выводили содержимое массива на экран. До этого, в таких случаях
мы повторно записывали ту же последовательность команд, в результате
чего наша программа становилась длиннее. А если вы допускали ошибки при
написании программ, то наверняка заметили, что чем длиннее программа – тем
сложнее в ней найти ошибку.
Но оказывается, что в таких случаях можно сократить
текст программы, оформив соответствующие последовательности команд в
виде вспомогательных алгоритмов, которые можно использовать многократно.
Вспомогательный алгоритм
– это алгоритм, который целиком использован в составе другого алгоритма.
Ещё одной важной особенностью вспомогательных
алгоритмов, является универсальность, то есть их можно использовать в
совершенно разных программах, в которых они будут работать одинаково, то есть
единожды написав, вспомогательный алгоритм вычисления площади треугольника,
можно его использовать в любой, программе, в которой в ходе работы требуется
вычислить площадь треугольника.
Задача: Робот находится в
левой верхней клетке поля без стен. Нарисовать девять квадратов. Две на две
клетки.
Очевидно, что при решении данной задачи мы будем
повторять одну и ту же последовательность команд для рисования каждого
квадрата. Следовательно, можно оформить её в качестве вспомогательного
алгоритма, а также у нас есть три одинаковых ряда квадратов,
последовательность команд для рисования которых можно так же оформить в виде вспомогательного
алгоритма.
Для начала запишем последовательность команд для
рисования квадрата в виде вспомогательного алгоритма, при этом
условимся, что все квадраты будем рисовать, начиная с левой верхней клетки.
Для этого, строкой ниже основного алгоритма запишем
служебное слово «алг» и название
вспомогательного алгоритма, назовём его «квадрат», а затем ниже,
служебные слова «нач» и «кон», между
которыми и будут находится команды для рисования квадрата.
Вспомогательный
алгоритм рисования квадрата
Так мы получили вспомогательный алгоритм
для рисования квадрата. Теперь запишем вспомогательный алгоритм для рисования
горизонтального ряда квадратов, назовём его ряд.
Чтобы нарисовать ряд квадратов, Робот
должен нарисовать первый квадрат, для этого вызовем уже написанный алгоритм,
записав его название. А затем нужно переместиться на позицию для рисования
следующего квадрата. Для этого Робот должен трижды сместиться вправо, и один
раз вверх. Далее нужно снова нарисовать квадрат и сместиться к следующему так
же, как и до этого, трижды сместившись вправо и один раз вверх, и снова
нарисовать квадрат.
Вспомогательный
алгоритм рисования ряда квадратов
Теперь у нас есть алгоритм для рисования ряда
квадратов. Запишем основной алгоритм. В нем нам можно сразу нарисовать ряд
квадратов, вызвав соответствующий вспомогательный алгоритм. Теперь нужно
переместиться на начальную позицию для рисования следующего ряда, для этого
достаточно переместиться в левый ряд и на две клетки вниз. То есть записать
цикл «пока слева свободно», содержащий команду «влево» и дважды команду «вниз».
Теперь нам нужно снова нарисовать ряд квадратов и переместиться на начальную
позицию, как мы делали до этого, записав цикл «пока слева свободно» с командой
«влево» и дважды команду «вниз» и наконец, снова нарисовать ряд квадратов.
Основной алгоритм
Запустим программу на выполнение. Девять
квадратов изображены верно, следовательно, задача решена.
Результат работы
программы
В блок-схеме вспомогательный алгоритм
изображается как показано на рисунке. Этот блок называется «Предопределённый
процесс», внутри него записывается название вспомогательного алгоритма, входные
и выходные параметры.
Изображение
вспомогательного алгоритма на блок-схеме
Задача: У нас есть вспомогательный
алгоритм factorial, который вычисляет значение
факториала целого числа k. Составить блок-схему алгоритма вычисления
значения выражения 1! + 2! + … + n!. Вспомним, что k! = 1 * 2 * … * k.
Блок-схема
вспомогательного алгоритма
Изобразим блок-схему данного алгоритма. В ней через i
обозначим порядковый номер слагаемого, для него же мы будем вычислять
факториал. Через а обозначим значение итого
слагаемого, а через r
— значение данного выражения. В начале нам нужно считать значение числа n и присвоить r значение 0, т.к. оно ещё не включает
ни одного слагаемого, затем будет идти цикл «Для i от 1 до n». В котором мы будем вычислять
значение i-того
слагаемого, используя вспомогательный алгоритм вычисления факториала, а затем
увеличивать на это значение r.
И в конце нам нужно вывести значение r.
Блок-схема
с использованием вспомогательного алгоритма
Рассмотрим, как работает вспомогательный алгоритм в
составе основного. В начале выполняются команды основного алгоритма, идущие
до вызова вспомогательного. Затем, когда доходит до выполнения вспомогательного
алгоритма, его формальные параметры, в нашем случае k, заменяются параметрами из основного
алгоритма. В нашем случае i. Далее выполняются
команды вспомогательного алгоритма. Затем значения выходных параметров
вспомогательного алгоритма, в нашем случае f подставляются в основной алгоритм, в
нашем случае в переменную a.
После чего далее выполняются команды основного алгоритма.
Через вспомогательные алгоритмы можно создавать так же
рекурсивные алгоритмы. Рекурсивным алгоритмом называется алгоритм,
который содержит ссылку на самого себя. Посмотрим для решения каких задач их
можно применить.
Мы можем составить вспомогательный алгоритм для
вычисления факториала, с использованием рекурсии, если примем во внимание
формулу: n!
= (n
— 1)!.
Важно при этом помнить, что 1! = 1. Блок-схема данного алгоритма будет
выглядеть так.
Блок-схема
рекурсивного алгоритма вычисления n!
Обратим внимание, что вспомогательный алгоритм содержит
ветвление, при котором, если n >
1
– n!
= (n
— 1)!,
а в случае если n
= 1,
то n!
= 1.
Также и в других рекурсивных алгоритмах, ссылка на алгоритм всегда
указывается лишь в одной ветви условного оператора, иначе он будет вызывать
сам себя бесконечно.
Задача: Робот находится в
поле без стен, на определённом расстоянии от левого края. Он должен нарисовать
уголок, то есть закрасить все клетки от своего текущего положения до левого
края, а потом столько же клеток вниз.
Запишем рекурсивный вспомогательный алгоритм для
рисования уголка. Назовём его угол. Он будет содержать условный
оператор, условием которого будет если слева свободно, если данное
условие выполняется, робот будет закрашивать клетку, в которой он находится и
смещаться на одну клетку влево, после чего снова вызывать себя. После условного
оператора будут содержаться команды, которые будут выполняться, когда робот
дойдёт до стены. На каждом шаге Робот должен закрасить клетку, в которой он
находится и сместиться на клетку вниз.
Рекурсивный
алгоритм рисования уголка
Основной алгоритм будет содержать только одну команду
— вызов вспомогательного алгоритма угол. Запустим программу на
выполнение. Робот действительно изобразил уголок.
Рассмотрим подробнее, как работает данный алгоритм.
Для примера возьмём случай, когда робот стоит в трёх клетках от левого
края поля. При первом вызове вспомогательного алгоритма условие выполняется,
следовательно, робот закрасит клетку в которой находится и сместиться на клетку
влево, после чего снова вызовет вспомогательный алгоритм для рисования уголка,
уже во второй раз. При втором вызове вспомогательного алгоритма робот
снова закрасит клетку, в которой находится, сместиться на клетку влево, и
вызовет себя уже в третий раз. При третьем вызове слева будет край поля,
следовательно, условие выполняться не будет, и выполнятся только команды,
которые идут после условного оператора, то есть робот закрасит клетку, в
которой находится и сместится на клетку вниз. При третьем вызове
вспомогательный алгоритм был завершён окончательно, а при первых двух – нет,
следовательно, сейчас будет продолжено выполнение второго вызова
вспомогательного алгоритма, то есть Робот снова закрасит клетку, в которой
находится и сместиться вниз. Второй вызов вспомогательного алгоритма завершён, осталось
выполнить до конца лишь первый вызов алгоритма. При этом Робот снова
закрасит клетку, в которой находится, и сместиться на клетку вниз. Уголок
готов.
Выполнение рекурсивного алгоритма, для
удобства можно представить в виде стека, то есть коробки, у
которой есть дно, но нет верхней крышки, в такую коробку объект можно
положить лишь поверх остальных, точно так же и достать из коробки можно
лишь верхний объект. То есть объект, который в коробку положили первым,
достанут из коробки последним. Так же происходит при выполнении
вспомогательного алгоритма угол, в нашем примере, в процессе выполнения первого
вызова алгоритма, он был вызван второй раз, а в процессе выполнения второго
вызова, в третий. После того, как было завершено выполнение третьего вызова,
было продолжено выполнение второго, а после его завершения – первого.
При использовании рекурсивных алгоритмов важно
помнить, что количество одновременных вызовов ограничено, поэтому, если
рекурсию можно заменить циклом – лучше так и поступить.
Важно
запомнить:
·
Вспомогательным
называется алгоритм, который целиком используется в составе другого алгоритма.
·
Рекурсивный алгоритм
– это алгоритм, в котором есть ссылка на самого себя.
·
Исполнение рекурсивного алгоритма можно
представить в виде стека.
·
Если рекурсию можно заменить циклом –
лучше так и поступить.
Мы научились
применять вспомогательные и рекурсивные алгоритмы при решении задач.
Информатика, 11 класс. Урок № 4.
Тема — Вспомогательные алгоритмы и подпрограммы: правила описания и использования подпрограмм
Перечень вопросов, рассматриваемых в теме: структурное программирование, подпрограммы, формальные параметры, фактические параметры, параметры-значения, параметры-переменные, процедуры, функции, рекурсия.
Глоссарий по теме: структурное программирование, подпрограммы, процедуры, функции, рекурсия.
Основная литература по теме урока:
Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 11 класса. — М.: БИНОМ. Лаборатория знаний, 2017
Дополнительная литература по теме урока:
— И. Г. Семакин, Т. Ю. Шеина, Л. В. Шестакова Информатика и ИКТ. Профильный уровень: учебник для 11 класса. — М.: БИНОМ. Лаборатория знаний, 2012
— Андреева Е. В. Программирование — это так просто, программирование — это так сложно. Современный учебник программирования. — М.: МЦНМО, 2015
— Молчанова С. И. Основы программирования. Турбо-Паскаль 7.0 для школьников и абитуриентов. — М.: «Аквариум»; ООО «Фирма «Издательство АСТ», 1999
Теоретический материал для самостоятельного изучения
На одном из прошлых уроков мы упоминали теорему, суть которой заключается в том, что для любой логической задачи можно составить алгоритм, используя лишь три базовых структуры: следование, ветвление и повторение. Эта теорема является одним из ключевых положений структурного программирования, о котором мы с вами сегодня и будем говорить.
Основные принципы структурного программирования заключаются в том, что:
- Любая программа строится из трёх базовых управляющих конструкций: последовательность, ветвление, цикл.
- В программе базовые управляющие конструкции могут быть вложены друг в друга произвольным образом.
- Повторяющиеся фрагменты программы можно оформить в виде подпрограмм. В виде подпрограмм можно оформить логически целостные фрагменты программы, даже если они не повторяются.
- Все перечисленные конструкции должны иметь один вход и один выход.
- Разработка программы ведётся пошагово, методом «сверху вниз».
Давайте узнаем, что такое подпрограммы, какими они могут быть и как их использовать.
На прошлом уроке мы рассмотрели один из базовых алгоритмов обработки числовых данных — алгоритм нахождения НОД натуральных чисел.
Вернемся к нему для решения задачи нахождения НОД трех натуральных чисел a, b, c. Для решения воспользуемся следующим математическим фактом: если a, b, c — три натуральных числа, то НОД (a, b, c) = НОД (НОД (a, b), c). Иначе говоря, нужно найти НОД двух величин, а затем НОД полученного значения и третьего числа.
Получаем:
Аналогичным образом можно было решить задачу нахождения НОД четырех, пяти и т. д. чисел. Понятно, что при этом код программы увеличился бы за счет добавления однотипных блоков. А можно ли каким-либо образом сократить запись алгоритма? Давайте разберемся.
В программировании ситуация, когда приходится выполнять одни и те же действия, является весьма типичной. Мы имеем алгоритм, который предназначен для решения подзадачи, выделенной в основной задаче. Выписывать алгоритм для решения подзадачи каждый раз заново в том месте программы, где он встречается, нерационально. Язык программирования Паскаль позволяет выделить любой алгоритм, описывающий подзадачу, и записать его только один раз, дав ему имя, а уже затем использовать его столько раз, сколько необходимо. Такой алгоритм называется подпрограммой и располагается в разделе описания до основной программы.
Подпрограммы подразделяются на процедуры (procedure) и функции (function).
Процедуры
Описание процедуры в Паскале имеет следующий формат:
Оформим в нашем примере в качестве процедуры подпрограмму нахождения НОД двух натуральных чисел.
Теперь разберемся, какая служебная информация находится в круглых скобка рядом с именем процедуры.
Подпрограмма реализует некоторый частный алгоритм, который вызывается в основной программе. Для реализации алгоритма подпрограмме могут понадобиться некоторые данные из основной программы. Обработав эти данные, подпрограмма возвращает результат основной программе, если в этом есть необходимость. Передавать информацию из основной программы в подпрограмму и наоборот мы можем только через переменные, которые носят специальное название — параметры. Именно они и указываются в круглых скобках рядом с именем процедуры.
Переменные, указанные непосредственно в заголовке процедуры, называются формальными параметрами. То, что подставляется вместо них при вызове процедуры в основной программе, называется фактическими параметрами:
Квадратные скобки указывают на то, что список формальных параметров может отсутствовать, т.е. возможна процедура без параметров. Параметры могут быть параметрами-переменными и параметрами-значениями. Параметры-переменные записываются следующим образом:
Параметры-значения указываются так:
Чаще всего параметры-значения служат для работы с входной в процедуру информацией, а параметры-переменные — для работы с выходной информацией.
Вернемся к программе nod1. Наша процедура evklid должна получить на вход две переменные, найти для них НОД и передать его в основную программу. Получаем:
Здесь мы замечаем, что наша процедура evklid дважды вызывается одинаковым образом. Но это нарушает саму идею решения и может привести к неверному ответу. Чтобы исправить эту ошибку, введем формальные параметры, имена которых отличны от фактических:
Теперь рассмотрим другой вариант программы, решающий ту же задачу. В ней используется процедура без параметров.
Чтобы разобраться в этом примере, введем одно важное понятие — область действия описания.
Областью действия описания любого программного объекта (переменной, типа, константы и т. д.) является тот блок, на который это описание распространяется. Если данный блок вложен в другой (подпрограмма), то присутствующие во вложенном блоке описания являются локальными. Они действуют только в пределах внутреннего блока. Описания же, расположенные во внешнем блоке, называются глобальными по отношению к внутреннему блоку. Если глобально описанный объект используется во внутреннем блоке, то на него распространяется внешнее (глобальное) описание.
В программе nod2 переменные x, y, nod1 являются локальными внутри процедуры; переменные a, b, c — глобальные. Однако внутри процедуры переменные a, b, c не используются. Связь между внешним блоком и процедурой осуществляется через параметры.
В программе nod2 все переменные являются глобальными. В процедуре evklid нет ни одной локальной переменной. Здесь обмен значениями между основной программой и процедурой осуществляется через глобальные переменные.
Функции
Теперь выясним, что такое подпрограмма-функция. Обычно функция используется в том случае, когда результатом работы подпрограммы должна быть скалярная (простая) величина. Тип результата называется типом функции.
Формат описания функции следующий:
Как и у процедуры, у функции служебная информация содержит список формальных параметров, среди которых могут присутствовать как параметры-значения, так и параметры-переменные. Все это — аргументы функции. Параметры могут вообще отсутствовать, если аргументы передаются глобально.
Программа решения рассмотренной выше задачи с использованием функции будет выглядеть следующим образом:
Сравнивая приведенные выше программы, можно сделать вывод, что программа nod4 имеет определенные преимущества перед другими. Функция позволяет получить результат путем выполнения одного оператора присваивания. Здесь также демонстрируется возможность того, что фактическим параметром при обращении к функции может быть эта же функция.
Рекурсия
Среди всевозможных подпрограмм особый интерес представляют так называемые рекурсивные подпрограммы.
Рекурсивная подпрограмма (функция, процедура) — подпрограмма, содержащая в своем описании вызов самой себя.
Пример 1. Как известно, факториал натурального числа определяется следующим образом:
n! = 1·2·3·…·n.
0! = 1.
Иначе это можно записать так:
F(n)=1 при n ≤ 1;
F(n)=F(n–1) · n при n > 1.
В определении факториала через рекурсию имеется условие n ≤ 1, при достижении которого вызов рекурсии прекращается. Такое условие (оно называется граничным) в рекурсивном определении должно присутствовать обязательно!
Пример 2. Алгоритм вычисления функции F(n), где n — натуральное число, задан следующими соотношениями:
F(n)=1 при n ≤ 2;
F(n)=F(n–1) +3· F(n–2) при n > 2.
Требуется выяснить, чему равно значение функции F(7).
По условию, F(1) = F(2) = 1.
F(3) = F(2) + 3 · F(1) = 1 + 3 · 1 = 4.
F(4) = F(3) + 3 · F(2) = 4 + 3 · 1 = 7.
F(5) = F(4) + 3 · F(3) = 7 + 3 · 4 = 19.
F(6) = F(5) + 3 · F(4) = 19 + 3 · 7 = 40.
F(7) = F(6) + 3 · F(5) = 40 + 3 · 19 = 97.
Подобные вычисления можно проводить в уме, а их результаты фиксировать в таблице:
И в завершение вспомним задачу вычисления НОД и модифицируем с использованием рекурсивной функции.
Применение рекурсивных методов для решения вычислительных задач не всегда эффективно. В большинстве случаев для решения той же задачи можно построить оптимальный не рекурсивный алгоритм. В то же время существуют задачи не вычислительного содержания, решить которые без использования рекурсии оказывается крайне проблематичным. К числу таких задач относится, например, известная головоломка под названием «Ханойские башни», с которой вы можете познакомиться в дополнительном материале.
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой

Была в сети 15.05.2023 05:23
Куропатова Жанна Николаевна
Учитель информатики и технологии
44 года
2 284
17 868
Вспомогательные алгоритмы чертежник
21.10.2019 02:11
Просмотр содержимого документа
«Вспомогательные алгоритмы чертежник»
Dcgjvfufntkmyst fkujhbnvs
Расшифруйте название темы
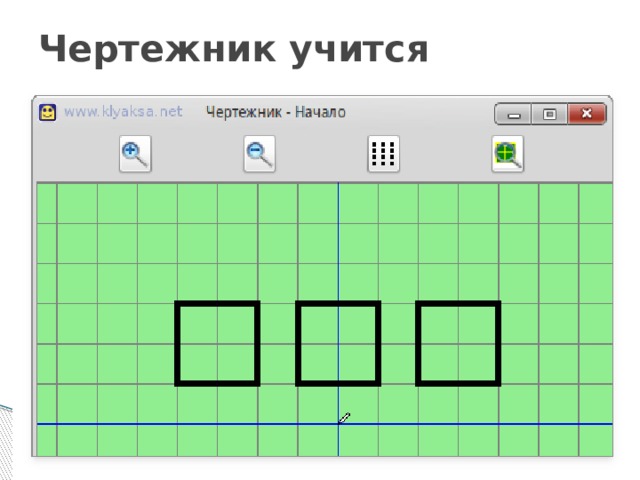
Чертежник учится
- использовать Чертежник алг квадраты 1 нач . сместиться в точку (-4,1) . опустить перо . сместиться на вектор (0,2) . сместиться на вектор (2,0) . сместиться на вектор (0,-2) . сместиться на вектор (-2,0) . поднять перо . сместиться в точку (-1,1) . опустить перо
- . сместиться на вектор (0,2) . сместиться на вектор (2,0) . сместиться на вектор (0,-2) . сместиться на вектор (-2,0) . поднять перо . сместиться в точку (2,1) . опустить перо . сместиться на вектор (0,2) . сместиться на вектор (2,0) . сместиться на вектор (0,-2) . сместиться на вектор (-2,0) . поднять перо . сместиться в точку (0,0) кон
Вспомогательные алгоритмы
- При построении новых алгоритмов нередко возникают ситуации, когда в разных местах алгоритма необходимо выполнение одной и той же последовательности шагов обработки данных. Для такой последовательности шагов создают отдельный алгоритм, называемый вспомогательным . В качестве вспомогательных могут использоваться алгоритмы, ранее разработанные для решения других задач.
Обращение к вспомогательному алгоритму
- Каждая процедура имеет свое уникальное имя. Вызов ВСА осуществляется с помощью вызова имени в основном алгоритме
- использовать Чертежник алг квадраты нач . сместиться в точку (-4,1) . квадрат . сместиться в точку (-1,1) . квадрат . сместиться в точку (2,1) . квадрат . сместиться в точку (0,0) кон
- Вспомогательный алгоритм записывается под основным алгоритмом
- алг квадрат нач . опустить перо . сместиться на вектор (0,2) . сместиться на вектор (2,0) . сместиться на вектор (0,-2) . сместиться на вектор (-2,0) . поднять перо кон
- использовать Чертежник алг квадраты нач . сместиться в точку (-4,1) . квадрат . сместиться в точку (-1,1) . квадрат . сместиться в точку (2,1) . квадрат . сместиться в точку (0,0) кон
- Использованный подход облегчает программирование сложных задач. Его называют метод последовательной (пошаговой) детализации.
- Другой метод заключается в том. Что создаются библиотеки подпрограмм и когда пишется основная программа, то она содержит обращения к ним. Такой метод называется сборочным программированием.
Задание
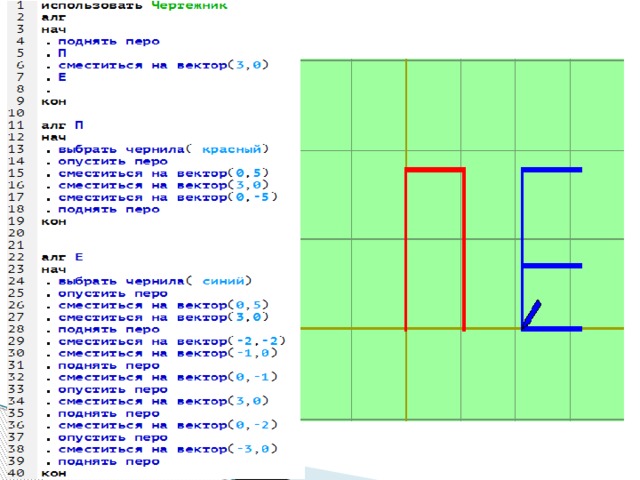
- 1. Составить для исполнителя программу с помощью которой можно написать буквы
- П,Е,Р,Т,И,О.
- 2. Используя в качестве ВСА буквы из предыдущего задания помогите исполнителю написать слова
- 1) Перо , 2) Порт, 3)Торт
Домашнее задание
- Используя программы для написания цифр из прошлого дз. Составьте программу рисования индексов городов Владивосток (690000), Елец (399770), Уссурийск (692500), Находка(692901), Дальнегорск (692441). В программе используйте вспомогательные алгоритмы.
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Тема: Вспомогательные алгоритмы и
подпрограммы
Цель: Обучить составлению вспомогательных
алгоритмов управления графическим учебным исполнителем.
Задачи:
Обучающие: дать понятие вспомогательного алгоритма,
подпрограммы (процедуры);
Развивающие: развитие алгоритмического мышления, памяти,
внимания, логического мышления, познавательного интереса, коммуникативной
культуры, учебно-познавательной компетенции;
Воспитательные: воспитание информационной
культуры учащихся, внимательности, аккуратности, дисциплинированности,
усидчивости.
Тип урока: урок изучения нового материала.
Изучаемые
вопросы:
Ø
Понятие вспомогательного
алгоритма и причины его использования.
Ø
Описание и вызов
вспомогательного алгоритма на алгоритмическом языке.
Ø
Метод последовательной
детализации.
Оборудование: компьютер, мультимедийный проектор.
Литература:
·
Семакин И.Г. «Информатика
и ИКТ. Базовый курс». Учебник для 8 класса. – М.: Бином. Лаборатория знаний,
2005. – 176 с.
·
Семакин И.Г. «Преподавание
базового курса информатики в средней школе: Методическое пособие». – 2-е изд.,
испр. и доп. – М.: Бином. Лаборатория знаний,2004. – 540с.
·
Методика преподавания
информатики: учеб. пособие для студ. пед. вузов / М.П.Лапчик, И.Г.Семакин,
Е.К.Хеннер. – 2-е изд., стер. – М.: Издательский центр «Академия», 2005. –
624с.
План:
1.
Организационный момент (2
мин)
2.
Актуализация знаний (7
мин)
3.
Изучение нового материала
(12 мин)
4.
Практическое задание(10
мин)
5.
Закрепление изученного
материала (10 мин)
6.
Итог урока (2 мин)
7.
Домашнее задание (2 мин)
8.
Ход урока:
1. Организационный момент
Учитель приветствует учеников, проверяет готовность
учеников к уроку и отмечает отсутствующих.
2. Актуализация знаний
Происходит виде устного опроса по следующим вопросам:
1.
Что такое алгоритм?
Откуда произошло это слово? (алгоритм – понятное и точное предписание
исполнителю выполнить конечную последовательность команд, приводящую от
исходных данных к искомому результату. Слово «алгоритм» происходит от имени
Мухаммеда аль-Хорезми, первым предложившего приемы выполнения арифметических
операций с многозначными числами.)
2.
Что такое исполнитель
алгоритма? (исполнитель алгоритма – это объект или субъект, для управления
которым составлен алгоритм)
3.
Что такое система команд
исполнителя? (СКИ – это совокупность команд, которые исполнитель умеет
выполнить.)
4.
В чем состоят основные
свойства алгоритма? (Алгоритм можно строить только из команд, входящих в СКИ
исполнителя – свойство понятности. Каждая команда алгоритма управления
определяет однозначное действие исполнителя – свойство точности. Выполнение
алгоритма должно приводить к результату за конечное число шагов – свойство
конечности)
5.
Какую работу может
выполнять ГРИС? ( ГРИС может перемещаться по полю и рисовать на этом поле)
6.
Что представляет собой
среда исполнителя ГРИС? (Среда исполнителя ГРИС это лист (страница экрана) для
рисования)
7.
Какие простые команды
входят в СКИ ГРИС; как они выполняются? (ШАГ- перемещение ГРИС на один шаг
вперед с рисованием линии; ПОВОРТ – поворот на 90 градусов против хода часовой
стрелки; ПРЫЖОК – перемещение на один шаг вперед без рисования линии.)
8.
В какой
последовательности происходит выполнение команд в линейном алгоритме? (В
линейном алгоритме команды выполняются по очереди, каждая только 1 раз).
3. Изучение нового материала
Пусть нам требуется решить некую задачу, по
которой Чертежник будет выводить четырехзначное число 1919.
|
|
|
|
|
|
Конечно, можно написать длинную
программу, по которой исполнитель шаг за шагом нарисует нам эти цифры.
Но возникает другой вопрос, ведь у нас присутствует
только две цифры 1 и 9 нельзя ли написать программу рисования одной и другой
цифры 1 раз? Это действительно сделать можно.
Для упрощения программирования сложных задач
используются вспомогательные алгоритмы.
Вспомогательный алгоритм — это алгоритм решения некоторой подзадачи из
исходной (основной) задачи.
В языках программирования вспомогательные
алгоритмы называют подпрограммами или процедурами.
Каждая процедура должна иметь свое уникальное
имя. Мы выберем ЕДИНИЦА и ДЕВЯТЬ.
Обращение к процедуре осуществляется по новой
команде из СКИ ГРИС. Команда обращения
к процедуре имеет формат,
т.е. общий вид, следующий:
сделай <имя процедуры>
Тогда в основной программе команды обращения к
этим процедурам будут сделай ЕДИНИЦА и сделай ДЕВЯТЬ.
Основная программа запишется в следующем виде:
программа число 1919
нач
сделай ЕДИНИЦА
прыжок
сделай ДЕВЯТЬ
прыжок
сделай ЕДИНИЦА
прыжок
сделай ДЕВЯТЬ
кон
Теперь надо «Объяснить» исполнителю,
что такое ЕДИНИЦА и что такое ДЕВЯТЬ. Это делается в описании процедур. Формат
описания процедуры:
процедура <имя процедуры>
нач
<тело процедуры>
кон
Имя в описании и имя в обращении должны точно
совпадать.
Запись процедур ЕДИНИЦА и ДЕВЯТЬ показана на
стр. 208 учебника.
Метод программирования, при котором сначала
записывается основной алгоритм, а затем описываются использованные в нем
вспомогательные алгоритмы, называется методом последовательной детализации, или программированием сверху вниз.
Метод программирования, при котором сначала
составляется множество подпрограмм, которые могут понадобиться при решении
задачи, а затем пишется основная программа, содержащая обращения к ним,
называется сборочным
методом, или программированием снизу вверх.
Подпрограммы могут быть объединены в библиотеку подпрограмм и сохранены в долговременной памяти
компьютера. Такую библиотеку можно постепенно пополнять новыми подпрограммами.
4. Практическое задание: Написать с использованием процедур программу
вывода на экран число 333
программа число 333
нач
сделай ТРИ
прыжок
сделай ТРИ
прыжок
сделай ТРИ
кон
Процедура ТРИ
нач
шаг
поворот
шаг
шаг
шаг
шаг
поворот
шаг
поворт
прыжок
прыжок
поворот
шаг
поворот
поворот
поворот
прыжок
прыжок
поворот
кон
5. Закрепление изученного материала
1.
Что такое вспомогательный
алгоритм? (Вспомогательный алгоритм — это алгоритм решения некоторой подзадачи из
исходной (основной) задачи.)
2.
Чем отличается
описание вспомогательного алгоритма от обращения к вспомогательному алгоритму? (описание
пишется вначале программы, а обращение это уже непосредственная ссылка на
строку с началом алгоритма.)
3.
Каковы правила
описания вспомогательных алгоритмов (процедур) для исполнителя ГРИС? (Имя в
описании и имя в обращении должны совпадать (никаких склонений по падежам).
Описание процедур располагается после самой программы)
4.
Как записывается
команда обращения к процедуре в языке исполнителя ГРИС? (Команда обращения к процедуре имеет формат, т.е. общий вид,
следующий: сделай <имя процедуры>)
5.
В чем суть метода
последовательной детализации? (Метод
программирования, при котором сначала записывается основной алгоритм, а затем
описываются использованные в нем вспомогательные алгоритмы, называется методом последовательной детализации, или программированием сверху вниз.)
6.
Что такое
программирование снизу вверх, сверху вниз? (Метод программирования, при
котором сначала записывается основной алгоритм, а затем описываются
использованные в нем вспомогательные алгоритмы, называется программированием
сверху вниз. Обратный порядок программирования называется программированием
снизу вверх.)
6. Подведение итогов урока: Итак, сегодня на уроке мы узнали что такое
вспомогательный алгоритм и для чего он используется, научились строить
алгоритмы с использованием процедур.
7. Домашнее задание: §42; выполнить задание №7